浙江省宁波市镇海区镇海蛟川书院2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、 $3 (x + 2) = 8$ B、 $3 x^{2} + 6 x = 8$ C、 $a x^{2} + b x + c = 0$ D、 $\frac{1}{x + 2} = 1$

查看试题解析
2. 奥运火炬时隔14年再次在“鸟巢”点燃，北京由此成为世界上首个既举办夏季奥运会又举办冬季奥运会的“双奥之城”，下列各届冬奥会会徽图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，将 $▱ A B C D$ 的一边 $B C$ 延长至点E，若 $∠ D C E = 62 °$ ，则 $∠ A$ 等于（）

A、 $62 °$ B、 $102 °$ C、 $118 °$ D、 $128 °$

查看试题解析
4. 如图，在 $△ A B C$ 中， $D$ 、 $E$ 分别是 $A B$ 、 $A C$ 边上的中点，若 $D E = 4$ ，则 $B C$ 等于（）

A、2 B、4 C、8 D、10

查看试题解析
5. 将方程 $2 x^{2} + 7 = 4 x$ 改写成 $a x^{2} + b x + c = 0$ 的形式，则a，b，c的值分别为（）

A、 $2$ ， $4$ ， $7$ B、 $2$ ， $4$ ， $- 7$ C、 $2$ ， $- 4$ ， $7$ D、 $2$ ， $- 4$ ， $- 7$

查看试题解析
6. 如图所示，满足函数 $y = k (x - 1)$ 和 $y = \frac{k}{x} (k \neq 0)$ 的大致图象是（）

A、①② B、②③ C、②④ D、①④

查看试题解析
7. 数学组老师在统计数学文化节志愿者参与情况时得到本次志愿者年龄情况统计如表：
年龄(岁)
$13$ 岁
$14$ 岁
$15$ 岁
$16$ 岁
人数(人)
$7$
$18$
$x$
$10 - x$
那么对于不同x的值，则下列关于年龄的统计量不会发生变化的是（）

A、平均数、方差 B、中位数、方差 C、平均数、中位数 D、众数、中位数

查看试题解析
8. 已知 $y_{1}$ 和 $y_{2}$ 均是以x为自变量的函数，当 $x = m$ 时，函数值分别为 $M_{1}$ 和 $M_{2}$ ，若存在实数m，使得 $M_{1} + M_{2} = 0$ ，则称函数 $y_{1}$ 和 $y_{2}$ 具有性质P.以下函数 $y_{1}$ 和 $y_{2}$ 具有性质P的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x - 1$ B、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = - x + 1$ C、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x - 1$ D、 $y_{1} = - \frac{1}{x}$ 和 $y_{2} = - x + 1$

查看试题解析
9. 如图，正方形纸片 $A B C D$ 的四个顶点分别在四条平行线 $a$ 、 $b$ 、 $c$ 、 $d$ 上，这四条直线中相邻两条之间的距离依次为 $h_{1}$ 、 $h_{2}$ 、 $h_{3} (h_{1} > 0 ， h_{2} > 0 ， h_{3} > 0)$ ，若 $h_{1} = 6$ ， $h_{2} = 3$ ，则正方形 $A B C D$ 的面积 $S$ 等于（）

A、 $90$ B、 $108$ C、 $117$ D、 $121$

查看试题解析
10. 如图，在一个大长方形中放入三个边长不等的小正方形 $①$ ， $②$ ， $③$ ，若要求两个阴影部分的周长差，只要知道下列哪两条线段的差的绝对值（）

A、 $| A B - C D |$ B、 $| C D - E F |$ C、 $| D E - C D |$ D、 $| D E - E F |$

查看试题解析

二、填空题

11. 若关于x的方程（c-1）x^|c^|+1+9x-4＝0是一元二次方程，则c＝.

查看试题解析
12. 一组数据的方差计算公式为 $s^{2} = \frac{1}{4} (5 - \bar{x})^{2} + (8 - \bar{x})^{2} + (8 - \bar{x})^{2} + (11 - \bar{x})^{2}]$ ，则这组数据的方差是.

查看试题解析
13. 如图，五边形 $A B C D E$ 是正五边形，若 $l_{1} / / l_{2}$ ，则 $∠ 1 - ∠ 2 =$ ．

查看试题解析
14. 如图，在菱形 $A B C D$ 中， $A B = 5$ ， $A C + B D = 14$ ，则菱形 $A B C D$ 的面积为.

查看试题解析
15. 如图，已知 $△ A B C$ 是边长为 $6$ 的等边三角形，点D是边 $B C$ 上的一点，且 $B D = 2$ ，以 $A D$ 为边作等边 $△ A D E$ ，过点E作EF//BC，交 $A C$ 于点F，连接 $B F$ ，则 $S_{四边形 B D E F} =$
.

查看试题解析
16. 如图，点A为直线 $y = - x$ 上一点，过A作 $O A$ 的垂线交双曲线 $y = \frac{k}{x} (x < 0)$ 于点B，若 $O A^{2} - A B^{2} = 16$ ，则k的值为.

查看试题解析

三、解答题

17. 解方程：

(1)、 $3 x^{2} - 6 x - 2 = 0$ .

(2)、 $(3 x - 1)^{2} = (x + 1)^{2}$ .

查看试题解析
18. 如图，在平面直角坐标系中，直线 $y = x + 3$ 与双曲线 $y = \frac{k}{x}$ 交于A，B两点，已知点A的横坐标为2.

(1)、求k的值；

(2)、求 $△ O A B$ 的面积；

(3)、直接写出关于 $x$ 的不等式 $x + 3 > \frac{k}{x}$ 的解集.

查看试题解析
19. 如图，在边长为 $1$ 个单位的正方形网格中， $△ A B C$ 经过平移后得到 $△ A^{'} B^{'} C^{'}$ ，点B的对应点为 $B^{'}$ ，根据下列条件，利用网格点和无刻度的直尺画图并解答，保留痕迹：

( 1 )画出 $△ A^{'} B^{'} C^{'}$ ，线段 $A C$ 扫过的图形的面积为____；

( 2 )在 $A^{'} B^{'}$ 的右侧确定格点Q，使 $△ A^{'} B^{'} Q$ 的面积和 $△ A B C$ 的面积相等，请问这样的Q点有____个？

查看试题解析
20. 《朗读者》自开播以来，以其厚重的文化底蕴和感人的人文情怀，感动了数以亿计的观众，某中学开展“朗读”比赛活动，九年级（1）、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示.

平均数

中位数

众数

九（1）班

85

85

九（2）班

80

(1)、根据图示填写表格.

(2)、结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好；

(3)、如果规定成绩较稳定班级胜出，你认为哪个班级能胜出？请说明理由.

查看试题解析
21. 如图，过 $△ A B C$ 的边 $A C$ 的中点O，作 $O E ⊥ A C$ ，交 $A B$ 于点E，过点A作 $A D ∥ B C$ ，与 $B O$ 的延长线交于点D，连接 $C D$ ， $C E$ ，若 $C E$ 平分 $∠ A C B$ ， $C E ⊥ B O$ 于点F.

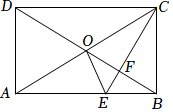(1)、求证： $△ O B C$ 是等腰三角形；

(2)、求证：四边形 $A B C D$ 是矩形.

查看试题解析
22. 2022年北京冬奥会吉祥物深受大家的喜欢，某特许零售店的冬奥会吉祥物销售量日益火爆．据统计，该店2022年1月的“冰墩墩”销量为1万件，2022年3月的“冰墩墩”销量为1.21万件．

(1)、求该店“冰墩墩”销量的月平均增长率；

(2)、该零售店4月将采用提高售价的方法增加利润，根据市场调研得出结论：如果将进
价80元的“冰墩墩”按每件100元出售，每天可销售500件，在此基础上售价每涨1元，那么每天的销售量就会减少10件，该零售店要想每天获得12000元的利润，且销量尽可能大，则每件商品的售价应该定为多少元？

查看试题解析
23. 给出如下新定义：在平面直角坐标系中，动点 $M (x ， y)$ 在反比例函数 $y_{1} = \frac{1}{x}$ 上，若点A绕着M点旋转 $180$ 度后得到点B，我们称B是A关于M的“伴随点”.

(1)、若M的横坐标为 $1$ ，则点 $A_{1} (2 ， 3)$ 关于M的“伴随点” $B_{1}$ 的所表示的点是；

(2)、若M的横坐标为 $2$ ，一次函数 $y_{2} = 2 x + 1$ 与该反比例函数 $y_{1} = \frac{1}{x}$ 的交点记为 $A_{2}$ ，则点 $A_{2}$ 关于M的“伴随点” $B_{2}$ 的所表示的点是；

(3)、若 $A_{3} (2 ， t)$ 关于M的“伴随点”为 $B_{3}$ ，由 $A_{3}$ 、 $B_{3}$ 和坐标原点构成的三角形为等腰直角三角形，且 $O A_{3}$ 为直角边，求t的值.

查看试题解析
24. 点P是线段 $A B$ 上的动点，分别以 $A P$ ， $B P$ 为边在 $A B$ 的同侧作正方形 $A P C D$ 与正方形 $P B E F$ .

(1)、如图1，连结 $A F$ 、 $B C$ ，判断 $A F$ 与 $C B$ 的位置关系和数量关系，并证明.

(2)、如图2，将正方形 $P B E F$ 绕点P逆时针旋转，使得点E落在线段 $B C$ 上， $E F$ 交 $P C$ 于点G，若 $D A = D F$ ， $A F = 10$ ，求 $S_{△ C E G}$ .

(3)、如图3，将方形 $P B E F$ 绕点P旋转至如图的位置，且 $A P = P B$ ，连结 $A F$ ，作 $∠ C P F$ 的角平分线交 $A F$ 于点H，请写出 $A H$ 、 $P H$ 、 $H F$ 之间的数量关系，并证明.

查看试题解析

年龄(岁)	$13$ 岁	$14$ 岁	$15$ 岁	$16$ 岁
人数(人)	$7$	$18$	$x$	$10 - x$

	平均数	中位数	众数
九（1）班	85		85
九（2）班		80