浙江省宁波市宁海县2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x^{2} = 0$ B、 $x^{2} = x (x + 1)$ C、 $2 x + \frac{1}{x} + 1 = 0$ D、 $x^{3} + x - 1 = 0$

查看试题解析
2. 下列图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列等式中，成立的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{{(- 5)}^{2}} = - 5$ C、 $\sqrt{2} \times \sqrt{6} = 2 \sqrt{3}$ D、 $4 \sqrt{3} - \sqrt{3} = 3$

查看试题解析
4. 一个多边形的每个外角等于40°.则这个多边形的边数为（）

A、6 B、9 C、10 D、12

查看试题解析
5. 下列关于平行四边形的特征的描述中，正确的个数有（）

(1)、对边相等；（2）对角相等；（3）对角线相等；（4）邻边相等；（5）邻角互补.

A、2个 B、5个 C、3个 D、4个

查看试题解析

6. 一家鞋店在一段时间内销售了某种女鞋30双，各种尺码鞋的销售量如下表所示：

鞋的尺码/ $cm$	22	22.5	23	23.5	24	24.5	25
销售量双	1	2	5	11	7	3	1

若每双鞋的销售利润相同，则该店主最应关注的销售数据是下列统计量中的（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析

7. 如图，若周长为20平行四边形ABCD的对角线AC，BD交于点O，且△ABO的周长比△BCO小2，则AB=（）.

A、4 B、6 C、9 D、11

查看试题解析
8. 关于x的一元二次方程（a﹣1）x²﹣2x﹣1＝0有两个实数根，则实数a的取值范围是（）

A、a≥0 B、a≥0且a≠1 C、a＞0 D、a＞0且a≠1

查看试题解析
9. 如图，四边形 $A O E F$ 是平行四边形，点 $B$ 为 $O E$ 的中点，延长 $F O$ 至点 $C$ ，使 $F O = 3 O C$ ，连接 $A B$ 、 $A C$ 、 $B C$ ，则在 $Δ A B C$ 中 $S_{Δ A B O} ： S_{Δ A O C} ： S_{Δ B O C}$ （）

A、 $6 ： 2 ： 1$ B、 $3 ： 2 ： 1$ C、 $6 ： 3 ： 2$ D、 $4 ： 3 ： 2$

查看试题解析
10. 如图，在平行四边形ABCD中，点F是BC上一点，BF＝6，CF＝2，点E是CD的中点，AE平分∠DAF， EF＝ $2 \sqrt{2}$ ，则△AEF的面积是（）

A、 $8 \sqrt{2}$ B、 $4 \sqrt{7}$ C、 $10 \sqrt{2}$ D、 $2 \sqrt{46}$

查看试题解析

二、填空题

11. 若 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知一组数据2，2，8，x，7，4的中位数为5，则x的值是．

查看试题解析
13. 已知 $(a^{2} + b^{2}) (a^{2} + b^{2} - 1)$ =6，则 $a^{2} + b^{2}$ 的值是．

查看试题解析
14. 疫情期间市民为了减少外出时间，许多市民选择使用手机软件在线上买菜，某买菜软件今年一月份新注册用户为300万，三月份新注册用户为432万，求二、三两个月新注册用户每月平均增长率．若设二、三两个月新注册用户每月平均增长率为x，则可列方程为．

查看试题解析
15. 如图，在平行四边形ABCD中，对角线AC，BD交于点O，AC⊥BC，若AB＝8，AD＝4，则BD的长为．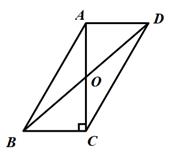

查看试题解析
16. 如图，在平行四边形ABCD中，BC=6，∠ABC=60°，BE平分∠ABC，点F为BC上一点，点G为BE上一点，连接CG，FG，则CG $+$ FG的最小值为．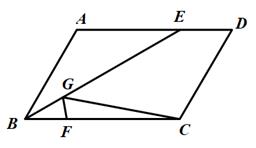

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{20} + {(- \sqrt{5})}^{2} -$ $\frac{1}{\sqrt{5}}$ ；

(2)、 $\sqrt{27} \times \sqrt{2} + {(\sqrt{2} - \sqrt{3})}^{2}$ .

查看试题解析
18. 解方程：

(1)、 $x^{2} - 3 x ＝ 0$ ；

(2)、 $2 x^{2} - 2 x + 2 ＝ 3 x$ .

查看试题解析
19. 如图，在6 $\times$ 8的网格图中，A，B，C三点都在格点上，按照如下要求找格点，

(1)、在图1中画出四边形ABCD为中心对称图形；

(2)、在图2中画出四边形ABCE为轴对称图形.

查看试题解析

20. 浙江某大学部分专业采用“三位一体”的形式进行招生，现有甲、乙两名学生，他们各自的三类成绩（已折算成满分100分）如表所示：

学生	学业水平测试成绩	综合测试成绩	高考成绩
甲	85	89	81
乙	88	81	83

(1)、如果根据三项得分的平均数，那么哪位同学排名靠前？

(2)、“三位一体”根据入围考生志愿，按综合成绩从高分到低分择优录取，综合成绩按“学业水平测试成绩×20%+综合测试成绩×20%+高考成绩×60%”计算形成，那么哪位同学排名靠前？

查看试题解析

21. 已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：EB∥DF．

查看试题解析
22. 2022年北京冬奥会吉祥物冰墩墩一开售，就深受大家的喜欢．某商店销售冰墩墩周边，每件冰墩墩周边进价60元，在销售过程中发现，当销售价为100元时，每天可售出30件，为庆祝冬奥会圆满落幕，该商店决定采取适当的降价措施，以扩大销售量增加利润，经市场调查发现，如果每件冰墩墩周边降价1元，平均可多售出3件.

(1)、若每件冰墩墩周边降价5元，商家平均每天能盈利多少元？

(2)、每件冰墩墩周边降价多少元时，能让利于顾客并且让商家平均每天能盈利1800元？

查看试题解析
23. 如图，在平面直角坐标系中，平行四边形OABC的顶点A的坐标为A（4，0），B的坐标为B（6，2）.

(1)、请直接写出平行四边形OABC的中心P的坐标；

(2)、求出直线PA的解析式；

(3)、试说明：不论k取何值，平行四边形OABC都被直线y=kx+1-3k分成面积相等的两部分.

查看试题解析
24. 如图，在四边形ABCD中， $A D ∥ B C$ ， $∠ B = 90 °$ ， $A B = 12 c m$ ， $A D = 15 c m$ ， $B C = 20 c m$ ，动点E从点A出发，在线段AD上以每秒1cm的速度向点D运动，动点F从点C出发，在线段CB上以每秒2cm的速度运动向点B运动，点E、F分别从点A、C同时出发，当点F运动到点B时，点E随之停止运动，设运动的时间为t（秒）.

(1)、用含t的代数式表示DE，DE=；

(2)、若四边形EFCD是平行四边形，求此时t的值；

(3)、是否存在点F，使△FCD是等腰三角形？若存在，请直接写出所有满足要求的t的值；若不存在，请说明理由.

查看试题解析