浙江省宁波市精准联盟2021-2022学年八年级下学期期中数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x - 2}$ 有意义，x的值可以是（）

A、2 B、1 C、0 D、-1

查看试题解析
2. 下列图案中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{(- 5)^{2}} = - 5$ B、 $5 \sqrt{3} \cdot 5 \sqrt{2} = 5 \sqrt{6}$ C、 $3 \sqrt{10} - 2 \sqrt{5} = \sqrt{5}$ D、 $\sqrt{7^{2}} = 7$

查看试题解析
4. 用配方法解方程x²+4x-5=0，下列配方正确的是（）

A、 $(x + 2)^{2} = 1$ B、 $(x + 2)^{2} = 5$ C、 $(x + 2)^{2} = 9$ D、 $(x + 4)^{2} = 9$

查看试题解析
5. 若n边形的内角和与外角和相加为 $1800 °$ ，则n的值为（）

A、7 B、8 C、9 D、10

查看试题解析
6. 用反证法证明三角形中至少有一个角不大于60°，应假设（）

A、三个角都小于60° B、三个角都大于60° C、三个角都大于或等于60° D、有两个角大于60°

查看试题解析
7. 某海鲜市场以每千克10元的进价进了一批螃蟹，经市场调研发现：售价为每千克20元时，每天可销售40千克.售价每上涨1元，每天的销量将减少3千克.如果该海鲜市场想平均每天获利408元，设这种螃蟹的售价上涨了x元，根据题意可列方程为（）

A、 $(x - 10) [40 - 3 (x - 20)] = 408$ B、 $(20 + x) (40 - 3 x) - 10 \times 40 = 408$ C、 $(20 + x) (40 - 3 x) = 408$ D、 $(20 + x - 10) (40 - 3 x) = 408$

查看试题解析
8. 在四边形ABCD中，AC、BD交于点O，在下列条件中，不能判定四边形ABCD为矩形的是（）

A、 $A O = C O$ ， $B O = D O$ ， $∠ B A D = 90 °$ B、 $A B = C D$ ， $A D = B C$ ， $A C = B D$ C、 $∠ B A D = ∠ B C D$ ， $∠ A B C + ∠ B C D = 180 °$ ， $A C ⊥ B D$ D、 $∠ B A D = ∠ A B C = 90 °$ ， $A C = B D$

查看试题解析
9. 如图，将平行四边形 $A B C D$ 沿对边上两点连线 $E F$ 对折，使点A恰好落在点C处，若 $∠ A B C = 120 °$ ， $A D = 4$ ， $A B = 8$ ，则 $A E$ 的长为（）.

A、4.6 B、 $4 \sqrt{3}$ C、5.6 D、 $5 \sqrt{3}$

查看试题解析
10. 如图，①②③④⑤五个平行四边形拼成一个含 $45 °$ 内角的菱形 $E F G H$ （不重叠无缝隙）.若①②③④四个平行四边形面积的和为 $14 \sqrt{2} c m^{2}$ ，四边形 $A B C D$ 面积是 $11 \sqrt{2} c m^{2}$ ，则①②③④四个平行四边形周长的总和为（）.

A、48 B、24 C、 $48 \sqrt{2}$ D、 $24 \sqrt{2}$

查看试题解析

二、填空题

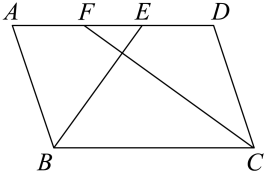
11. 点（﹣4，3）关于原点对称的点的坐标是．

查看试题解析
12. 甲、乙、丙、丁四名同学进行跳高测试，每人10次跳高成绩的平均数都是 $1.28 m$ ，方差分别是 ${S_{甲}}^{2} = 0.63 m^{2} ， {S_{乙}}^{2} = 0.61 m^{2} ， {S_{丙}}^{2} = 0.57 m^{2} ， {S_{丁}}^{2} = 0.56 m^{2}$ ，则这四名同学成绩最稳定的是.

查看试题解析
13. 如果 $y = \sqrt{x - 2} + \sqrt{2 - x} + 5$ ，那么 $y^{x}$ 的值是，

查看试题解析
14. 目前以5G等为代表的战略性新兴产业蓬勃发展.某市2020年底有5G用户2万户，计划到2022年底全市5G用户数累积到达到9.5万户.设全市5G用户数年平均增长率为x，则x的值为.

查看试题解析
15. 如图，在 $▱ A B C D$ 中， $A B = 10 ， B C = 18 ， ∠ A B C$ 和 $∠ B C D$ 的角平分线分别交 $A D$ 于点E和F，若 $B E = 12$ ，则 $C F =$ .

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A B = 3$ ， $A D = 4$ ， E为线段 $B C$ 上一动点，作点B关于 $A E$ 的轴对称点F，连接 $E F$ ， $D F$ ， G为 $D F$ 中点.当D，F，E三点共线时， $C E$ 的长为；在E的整个运动过程中，C，G两点距离的最小值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{27} - \sqrt{48} + \sqrt{\frac{1}{3}}$ ；

(2)、 $(\sqrt{24} - \sqrt{\frac{3}{8}}) \times \sqrt{2}$ .

查看试题解析
18. 解下列方程：

(1)、x²-3x=（3-x）²；

(2)、2x²+4x-7=0.

查看试题解析
19. 某学校为了了解本校1000名学生的课外阅读的情况，现从各年级随机抽取了部分学生，对他们一周的课外阅读时间进行了调查，并绘制出如下的统计图1和图2，根据相关估息，解答下列问趣：

(1)、本次接受随机抽样调查的学生人数为，图①中m的值为；

(2)、本次调查获取的样本数据的众数为，中位数为，平均数为；

(3)、根据样本的数据，估计该校一周的课外阅读时间大于5h的学生人数人数.

查看试题解析
20. 图①，图②是两张形状和大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，线段 $A B$ 的两个端点均在小正方形的顶点上.

(1)、请在图①中画一个以A，B为顶点，面积为6的平行四边形（非矩形），点C，D在格点上.

(2)、请在图②中画一个以A，B为顶点，面积为6的矩形，点C，D在格点上.

查看试题解析
21. 已知：关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 1 = 0$ .

(1)、判断方程的根的情况；

(2)、若 $△ A B C$ 为等腰三角形， $A B = 5 c m$ ，另外两条边长是该方程的根，求 $△ A B C$ 的周长.

查看试题解析
22. 如图，菱形ABCD的对角线AC和BD交于点O，分别过点C、作CE $∥$ BD，DE $∥$ AC，CE和DE交于点E

(1)、求证：四边形ODEC是矩形；

(2)、当∠ADB＝60°，AD＝10时，求CE和AE的长．

查看试题解析
23. 园林部门计划在某公园建一个长方形苗圃 $A B C D$ .苗圃的一面靠墙（墙最大可用长度为14米）.另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门（门不用木栏），建成后所用木栏总长32米，设苗圃 $A B C D$ 的一边 $C D$ 长为x米.

(1)、 $B C$ 长为米（包含门宽，用含x的代数式表示）；

(2)、若苗圃 $A B C D$ 的面积为 $96 m^{2}$ ，求x的值；

(3)、当x为何值时，苗圃 $A B C D$ 的面积最大，最大面积为多少？

查看试题解析
24. 问题原型

(1)、如图1，在菱形 $A B C D$ 中， $∠ B = 60 °$ ， $A E ⊥ B C$ 于E，F为 $C D$ 中点，连结 $A F$ ， $E F$ .试猜想 $△ A E F$ 的形状，并说明理由.

(2)、如图2，在 $▱ A B C D$ 中， $A E ⊥ B C$ 于E，F为 $C D$ 中点，连结 $A F$ ， $E F$ .试猜想 $△ A E F$ 的形状，并说明理由.

(3)、如图3，在 $▱ A B C D$ 中，F为 $C D$ 上一点，连结 $B F$ ，将 $∠ C$ 沿 $B F$ 折叠，点C的对应点为 $C^{'}$ .连结 $D C^{'}$ 并延长交 $A B$ 于G，若 $A G = C^{'} F$ ，求证：F为 $C D$ 中点.

(4)、如图4，直角坐标系中有 $▱ A B C D$ ，点A与原点重合，点B在x轴正半轴上， $C D$ 与y轴交于点E.将其沿过A的直线折叠，点B对应点 $B^{'}$ 恰好落在y轴上，且折痕交 $B C$ 于M， $B^{'} M$ 交 $C D$ 于点N.若 $▱ A B C D$ 的面积为48， $A B = 8$ ， $A D = 3 \sqrt{5}$ ，求点M的坐标和阴影部分面积（直接写出结果）.

查看试题解析