浙江省宁波市海曙区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

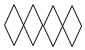
1. 在下列图形中，不能通过其中一个四边形平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，是关于x，y的二元一次方程的是（）

A、 $3 x ＋ y$ B、 $x - 5 y ＝ 12$ C、 $2 x y ＋ y ＝0$ D、 $\frac{5}{x} - y ＝ 1$

查看试题解析
3. 下列运算正确的是（）.

A、 $a^{3} \cdot a^{4} = a^{12}$ B、 $(- 2 a^{2} b^{3})^{3} = - 2 a^{6} b^{9}$ C、 $a^{6} \div a^{3} = a^{3}$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
4. 下列各式能用平方差公式计算的是（）

A、 $(- a + b) (- a - b)$ B、 $(a + b) (a - 2 b)$ C、 $(- a + b) (a - b)$ D、 $(- a - b) (a + b)$

查看试题解析
5. 如图，有一块含有45°角的直角三角板的两个顶点放在直尺的对边上，则 $∠ 1 ＋ ∠ 2 ＝$ （）

A、 $3 0^{∘}$ B、 $4 5^{∘}$ C、 $2 5^{∘}$ D、 $1 5^{∘}$

查看试题解析
6. 已知 $a^{x} ＝ 3 ， a^{y} ＝ 2$ ，则 $a^{2 x - 3 y} =$ （）

A、 $\frac{3}{4}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{9}{8}$

查看试题解析
7. 如图，在一块边长为a的正方形花圃中，两纵两横的4条宽度为b的人行道把花圃分成 9块，下面是四个计算种花土地总面积的代数式：（1） $(a - 2 b) (a - 2 b)$ ；（2） $a^{2} - 4 a b$ ；（3） $a^{2} - 4 a b - 4 b^{2}$ ；（4） $a^{2} - 4 a b + 4 b^{2}$ ，其中正确的有（）

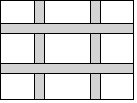A、（2） B、（1）（3） C、（1）（4） D、（4）

查看试题解析
8. 甲乙两人在相距18千米的两地，若同时出发相向而行，经2小时相遇；若同向而行，且甲比乙先出发1小时，那么在乙出发后经4小时甲追上乙，求甲、乙两人的速度.设甲的速度为x千米/小时，乙的速度为y千米/小时，则可列方程组为（）

A、 $\{\begin{cases} 2 x - 2 y = 18 \\ 5 x + 4 y = 18 \end{cases}$ B、 $\{\begin{cases} 2 x + 2 y = 18 \\ 5 x - 4 y = 18 \end{cases}$ C、 $\{\begin{cases} 2 x + 2 y = 18 \\ 4 y - 5 x = 18 \end{cases}$ D、 $\{\begin{cases} 2 x + 2 y = 18 \\ 5 x + 4 y = 18 \end{cases}$

查看试题解析
9. 若 $x^{2} - 2 (m - 1) x + 9$ 是完全平方式，则m的值为（）

A、4 B、2或 $- 4$ C、 $\pm 6$ D、 $- 2$ 或4

查看试题解析
10. 如图， $△ A B C$ 中， $∠ B = 90 ° ， ∠ A = 30 ° ， E ， F$ 分别是边 $A B ， A C$ 上的点，连接 $E F$ ，将 $△ A E F$ 沿着者 $E F$ 折叠，得到 $△ A^{'} E F$ ，当 $△ A^{'} E F$ 的三边与 $△ A B C$ 的三边有一组边平行时， $∠ A E F$ 的度数不可能是（）

A、 $120 °$ B、 $105 °$ C、 $75 °$ D、 $45 °$

查看试题解析

二、填空题

11. 若 $x^{2} - y^{2} = 30$ ，且 $x + y = 5$ ，则 $x - y =$ .

查看试题解析
12. 计算： $(π - 2)^{0} + (- 1)^{2023} + (\frac{1}{2})^{- 3} =$ .

查看试题解析
13. 已知 $x + y = - 5 ， x y = 3$ ，则 $x^{2} + y^{2} =$ .

查看试题解析
14. 已知方程组 ${\begin{array}{l} a x + b y = 4 \\ b x + a y = 5 \end{array}$ 的解是 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则 $a - b$ 的值为.

查看试题解析
15. 如图是由截面为同一种长方形的墙砖粘贴的部分墙面，其中三块横放的墙砖比一块竖放的墙砖高 $10 c m$ ，两块横放的墙砖比两块竖放的墙砖低 $40 c m$ ，则每块墙砖的截面面积是 .

查看试题解析
16. 已知长方形 $A B C D ， A D > A B ， A D = 10$ ，将两张边长分别为 $a$ 和 $b (a > b)$ 的正方形纸片按图1，图2两种方式放置（图1，图 2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $S_{1}$ ，图2中阴影部分的面积为 $S_{2}$ .当 $S_{1} - S_{2} = 3$ 时， $A B$ 的值是.

查看试题解析

三、解答题

17. 解方程组：

(1)、 ${\begin{array}{l} 3 x + 2 y = 10 \\ y = 2 - x \end{array}$

(2)、 ${\begin{array}{l} 2 x - 7 y = 5 \\ 3 x - 8 y = 10 \end{array}$

查看试题解析
18. 计算：

(1)、 $(x - \frac{1}{2} y)^{2}$

(2)、 $(3 a + b - 2) (3 a - b + 2)$

查看试题解析
19. 已知多项式 $A = (3 - 2 x) (1 + x) + (3 x^{5} y^{2} + 4 x^{6} y^{2} - x^{4} y^{2}) \div (x^{2} y)^{2}$

(1)、化简多项式 A；

(2)、若 $(x + 1)^{2} = 6$ ，求 A 的值.

查看试题解析
20. 如图，∠EFC+∠BDC=180°，∠DEF=∠B

(1)、求证：∠ADE=∠DEF；

(2)、判定 DE 与 BC 的位置关系，并说明理由.

查看试题解析
21. 今年，新型冠状病毒来势汹汹，疫情刻不容缓.某医用材料厂紧急召回放假的工人生产防病毒口罩，已知甲车间和乙车间共同生产3天可完成336万只，且甲车间比乙车间每天少生产56万只.

(1)、求甲车间和乙车间每天各生产防病毒口罩多少万只？

(2)、甲车间和乙车间准备共同完成840万只防病毒口罩的任务，在甲、乙车间合作生产了2天后，为了应对疫情的发展，医用材料厂的领导决定加快速度生产，结果余下的任务恰好用了5天完成，求该医用材料厂加快速度生产后的日产量比未加快速度的日产量多多少万只？

查看试题解析
22. 数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助助理解数学问题.

(1)、请写出图1，图2，图3阴影部分的面积分别能解释的乘法公式.
图1 ，图2 ，图3.

(2)、用4个全等的长和宽分别为 $a ， b$ 的长方形拼摆成一个如图4的正方形，请你通过计算阴影部分的面积，写出这三个代数式 $(a + b)^{2} ， (a - b)^{2} ， a b$ 之间的等量关系.

(3)、根据（2）中你探索发现的结论，计算：当 $a + b = 5 ， a b = - 6$ 时，求 $a - b$ 的值.

查看试题解析
23. 把 $y = a x + b$ （其中a、b是常数，x、y是未知数）这样的方程称为“雅系二元一次方程”.当 $y = x$ 时，“雅系二元一次方程 $y = a x + b$ ”中x的值称为“雅系二元一次方程”的“完美值”.例如：当 $y = x$ 时，雅系二元一次方程“ $y = 3 x - 4$ ”化为 $x = 3 x - 4$ ，其“完美值”为 $x = 2$ .

(1)、“雅系二元一次方程 $y = - 5 x + 6$ ”的“完美值”是；

(2)、 $x = 3$ 是“雅系二元一次方程“ $y = 3 x + m$ ”的“完美值”，求m的值；

(3)、“雅系二元一次方程 $y = k x + 1$ （ $k \neq 0$ ， k是常数）”存在“完美值”吗？若存在，请求出其“完美值”，若不存在，请说明理由.

查看试题解析
24. 如图，已知AB∥CD，P是直线AB，CD间的一点，PF⊥CD于点F，PE交AB于点E，∠FPE＝120°.

(1)、∠AEP的度数为.

(2)、如图2，射线PN从PF出发，以每秒40°的速度绕P点按逆时针方向旋转，当PN垂直AB时，立刻按原速返回至PF后停止运动；射线EM从EA出发，以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动.若射线PN，射线EM同时开始运动，设运动时间为t秒.
①当∠MEP＝20°时，求∠EPN的度数；
②当EM∥PN时，求t的值.

查看试题解析