浙江省金华市义乌市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是二元一次方程的是（）

A、 $\frac{x}{3}$ - $\frac{5}{2}$ y=6 B、 $\frac{2}{x}$ + $\frac{1}{y}$ =1 C、3x-y²=0 D、4xy=3

查看试题解析
2. 下列运算正确的是（）

A、 $a^{4} + a^{5} = a^{9}$ B、 $a^{3} \cdot a^{3} \cdot a^{3} = 3 a^{3}$ C、 $2 a^{4} \times 3 a^{5} = 6 a^{9}$ D、 $(- a^{3})^{4} = a^{7}$

查看试题解析
3. 如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）

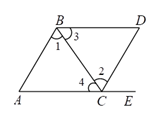A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°

查看试题解析
4. 如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（）

A、a户最长 B、b户最长 C、c户最长 D、三户一样长

查看试题解析
5. 已知 $x - \frac{1}{x} = 4$ ，则 $x^{2} + \frac{1}{x^{2}}$ 的值是（）

A、18 B、16 C、14 D、12

查看试题解析
6. 如图，点E、F分别是AB、CD上的点，点G是BC的延长线上一点，且∠B=∠DCG=∠D，则下列判断错误的是（）

A、∠ADF=∠DCG B、∠A=∠BCF C、∠AEF=∠EBC D、∠BEF+∠EFC=180°

查看试题解析
7. 因H7N9禽流感致病性强，某药房打算让利于民，板蓝根一箱原价为100元，现有下列四种调价方案，其中0＜n＜m＜100，则调价后板蓝根价格最低的方案是（）

A、先涨价m%，再降价n% B、先涨价n%，再降价m% C、先涨价 $\frac{m + n}{2} %$ ，再降价 $\frac{m + n}{2} %$ D、无法确定

查看试题解析
8. 下列语句：①同一平面上，三条直线只有两个交点，则三条直线中必有两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（　　）

A、①、②是正确的命题 B、②、③是正确命题 C、①、③是正确命题 D、以上结论皆错

查看试题解析
9. 已知a-b＝2，a-c＝ $\frac{1}{2}$ ，则代数式（b-c）²+3（b-c）+ $\frac{9}{4}$ 的值是（）

A、- $\frac{3}{2}$ B、 $\frac{3}{2}$ C、0 D、 $\frac{9}{4}$

查看试题解析
10. 7张如图1的长为a，宽为 $b (a > b)$ 的小长方形纸片，按图2的方式不重叠地放在矩形 $A B C D$ 内，未被覆盖的部分（两个矩形）用阴影表示，设左上角与右下角的阴影部分的面积的差为S，当 $B C$ 的长度变化时，按照同样的故置方式，S始终保持不变，则a，b满足（）

A、 $a = b$ B、 $a = 3 b$ C、 $a = 2 b$ D、 $a = 4 b$

查看试题解析

二、填空题

11. $(- 8)^{2012} \times (0.125)^{2013}$ ＝.

查看试题解析
12. 二元一次方程3x+2y=15的正整数解为

查看试题解析
13. 如图，直线l₁//l₂ ， AB⊥CD，∠1=40°，则∠2=.

查看试题解析
14. 如图，面积为12cm²的△ABC沿BC方向平移至△DEF位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积是cm² ．

查看试题解析
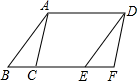15. 如图，AB∥CD， AD∥BC，点E、F分别是线段BC和CD上的动点，在两点运动到某一位置时，恰好使得∠AEF=∠AFE ，此时量得∠BAE=15°，∠FEC=12°，∠DAF=25°，则∠EFC=°．

查看试题解析
16. 已知a²+1＝3a，b²+1＝3b，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ ＝.

查看试题解析

三、解答题

17. 解方程：

(1)、 ${\begin{array}{l} 2 x - y = 4 \\ \frac{x}{3} + \frac{y}{2} = 8 \end{array}$ ；

(2)、 ${\begin{array}{l} x + 2 y = 0 \\ 2 x - y = 5 \end{array}$ .

查看试题解析
18. 将下面的解答过程补充完整：
如图，点 $E$ 在 $D F$ 上，点 $B$ 在 $A C$ 上， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ .试说明： $A C ∥ D F$ .
解：∵ $∠ 1 = ∠ 2$ （已知）
$∠ 1 = ∠ 3$ （             ）
∴ $∠ 2 = ∠ 3$ （             ）
∴  ▲   $∥$   ▲  （             ）
∴ $∠ C = ∠ A B D$ （             ）
∵ $∠ C = ∠ D$ （已知）
∴ $∠ D = ∠ A B D$ （             ）
∴ $A C ∥ D F$ （             ）

查看试题解析
19. 如图，AB//CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，求∠F的度数.

查看试题解析
20. 你会求（a－1）（a²⁰¹²＋a²⁰¹¹＋a²⁰¹⁰＋‥‥a²＋a＋1）的值吗？这个问题看上去很复杂，我们可以先考虑简单的情况，通过计算，探索规律：
（a－1）（a＋1）＝a²－1
（a－1）（a²＋a＋1）＝a³－1；
（a－1）（a³＋a²＋a＋1）＝a⁴－1；

(1)、由上面的规律我们可以大胆猜想，得到（a－1）（a²⁰¹²＋a²⁰¹¹＋a²⁰¹⁰＋……a²＋a＋1）＝.

(2)、利用上面的结论，求2²⁰¹³＋2²⁰¹²＋2²⁰¹¹＋……2²＋2＋1的值是.

(3)、求5²⁰¹³＋5²⁰¹²＋5²⁰¹¹＋……5²＋5＋1的值.

查看试题解析
21. 如图

(1)、如图1，将长方形纸片ABFE沿着线段DC折叠，CF交AD于点H，过点H作HG∥DC，交线段CB于点G．
①判断∠FHG与∠EDC是否相等，并说明理由；

②说明HG平分∠AHC的理由．

(2)、如图2，如果将(1)中的已知条件改为折叠三角形纸片ABE，其它条件不变．HG是否平分∠AHC？如果平分请说明理由；如果不平分，请找出∠CHG，∠AHG与∠E的数量关系并说明理由．

查看试题解析
22. 甲、乙两个学校乐团，决定向某服装厂购买同样的演出服.下面是服装厂给出的演出服装的价格表：经调查：两个乐团共75人（甲乐团人数不少于40人），如果分别各自购买演出服，按每人一套的标准两个乐团共需花费5600元.请回答以下问题：
购买服装的套数
1~39套（含39套）
40~79套（含79套）
80套及以上
每套服装的价格
80元
70元
60元

(1)、如果甲、乙两个乐团联合起来购买服装，那么比各自购买服装最多可以节省多少元？

(2)、甲、乙两个乐团各有多少人？

(3)、现从甲乐团抽调a人，从乙乐团抽调b人（要求从每个乐团抽调的人数不少于5人），去儿童福利院献爱心演出，并在演出后每位乐团成员向儿童们进行“心连心活动”；甲乐团每位成员负责3位小朋友，乙乐团每位成员负责5位小朋友，这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案，并说明理由.

查看试题解析
23. 利用我们学过的知识，可以导出下面这个形式优美的等式： $a^{2} + b^{2} + c^{2} - a b - b c - a c = \frac{1}{2} [{(a - b)}^{2} + {(b - c)}^{2} + {(a - c)}^{2}]$ ，该等式从左到右的变形，不仅保持了结构的对称性，还体现了数学的和谐、简洁美；

(1)、请你检验说明这个等式的正确性.

(2)、若 $a = 2011 ， b = 2012 ， c = 2013$ ，你能很快求出 $a^{2} + b^{2} + c^{2} - a b - b c - a c$ 的值吗？

(3)、若 $a - b = \frac{3}{5} ， b - c = \frac{3}{5} ， a^{2} + b^{2} + c^{2} = 1$ ，求 $a b + b c + a c$ 的值.

查看试题解析
24. 如图，已知直线a⊥直线b，垂足为点O.将直角三角形纸板ABC的直角边AC放置在直线a上，线段AB（或射线AB）与直线b交于点D，直线CE//AB交直线b于点E，AF平分∠DAO，EF平分∠DEC.设∠BAC=x度，∠ABC=y度，且x：y=1：2.

(1)、求x、y的值及∠ADO的度数；

(2)、如图1，当A、C两点在点O的两侧时，求∠AFE的度数；

(3)、将（2）中的三角形纸板沿CA方向平移，当A、C两点都移动到点O的左侧时如图2，请按题意在图2中画出图形，并判断∠AFE的度数与（2）的结果比较是否改变？若改变，直接写出此时∠AFE的度数；若不变，请说明理由.

查看试题解析

购买服装的套数	1~39套（含39套）	40~79套（含79套）	80套及以上
每套服装的价格	80元	70元	60元