浙江省杭州市十三中教育集团(总校)2021-2022学年七年级下学期期中数学试题
试卷更新日期:2023-03-29 类型:期中考试
一、单选题
-
1. 下列方程中,是二元一次方程的是( )A、3x-2y=4z B、4x+y=2 C、 D、6xy+9=02. 数科学记数法表示为( )A、 B、 C、 D、3. 下列等式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,能判断ABCE的条件是( )
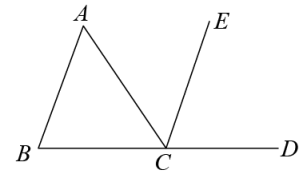 A、∠A=∠ACE B、∠A=∠ECD C、∠B=∠BCA D、∠B=∠ACE6. 已知 , , 则的值为( )A、6 B、 C、0 D、17. 如图,小区大门的栏杆AB垂直地面AE于A点,CD平行于地面AE,那么∠ABC+∠BCD=( )
A、∠A=∠ACE B、∠A=∠ECD C、∠B=∠BCA D、∠B=∠ACE6. 已知 , , 则的值为( )A、6 B、 C、0 D、17. 如图,小区大门的栏杆AB垂直地面AE于A点,CD平行于地面AE,那么∠ABC+∠BCD=( ) A、315° B、225° C、200° D、270°8. 已知 , , 则的值为( )A、24 B、36 C、72 D、69. 已知关于x、y的方程组的解是 , 则关于x、y的方程组的解是( )A、 B、 C、 D、10. 如图, , 点E为上方一点,分别为的角平分线,若 , 则的度数为( )
A、315° B、225° C、200° D、270°8. 已知 , , 则的值为( )A、24 B、36 C、72 D、69. 已知关于x、y的方程组的解是 , 则关于x、y的方程组的解是( )A、 B、 C、 D、10. 如图, , 点E为上方一点,分别为的角平分线,若 , 则的度数为( )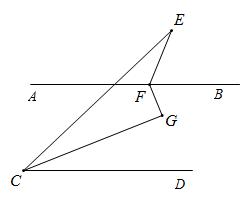 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:.12. 计算:.13. 如图,直线a∥b,∠1=120°,则∠2的度数为 .
 14. 某种电器产品,每件若以原定价的8折销售,可获利120元;若以原定价的6折销售,则亏损20元,该种商品每件的进价为 元.15. 如图,将一张长方形纸条折叠,若 ,则 的度数为.
14. 某种电器产品,每件若以原定价的8折销售,可获利120元;若以原定价的6折销售,则亏损20元,该种商品每件的进价为 元.15. 如图,将一张长方形纸条折叠,若 ,则 的度数为. 16. 已知x,y满足方程组.给出下列结论:①当时,方程组的解也是的解;②若方程组的解满足 , 则;③无论k为何值,;④若 , 则或.正确的是.
16. 已知x,y满足方程组.给出下列结论:①当时,方程组的解也是的解;②若方程组的解满足 , 则;③无论k为何值,;④若 , 则或.正确的是.三、解答题
-
17. 计算:(1)、(2)、18. 解下列方程组(1)、(2)、19.(1)、化简:;(2)、若a满足条件求(1)中代数式的值.20. 在所给的网格图(每个小格均为边长是1的正方形)中完成下列各题:
 (1)、先将向右平移4格,再向下平移3格,请作出两次平移后所得的;(2)、连结 , , 判断与的关系,并求四边形的面积.21. 如图,在中,点在上,点在上,点在上,且 , .
(1)、先将向右平移4格,再向下平移3格,请作出两次平移后所得的;(2)、连结 , , 判断与的关系,并求四边形的面积.21. 如图,在中,点在上,点在上,点在上,且 , . (1)、求证:;(2)、若平分 , 平分 , 且 , 求的度数.22. 已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:(1)、1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?(2)、请帮助物流公司设计租车方案(3)、若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.23. (1)请用两种不同的方法表示图中阴影部分的面积和.
(1)、求证:;(2)、若平分 , 平分 , 且 , 求的度数.22. 已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:(1)、1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?(2)、请帮助物流公司设计租车方案(3)、若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.23. (1)请用两种不同的方法表示图中阴影部分的面积和.
方法1:____;
方法2:____.
(1)、请你直接写出三个代数式: , , ab之间的等量关系.(2)、根据(2)中的等量关系,解决如下问题:①已知 , , 求mn和的值;
②已知 , 求的值.