浙江省杭州市三校2021-2022学年七年级下学期期中检测数学试题

试卷更新日期：2023-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $2^{6} \div 2^{3} = 2^{2}$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 $(- 3)^{2} \times (- 3)^{3} = 3^{5}$ D、 $x^{3} \cdot x^{5} = x^{8}$

查看试题解析
2. 下列各式中，是关于x，y的二元一次方程的是（　　）

A、x-2y＝3 B、x+xy-3＝0 C、2x+y D、 $\frac{2}{x}$ -y＝1

查看试题解析
3. 如图，直线EF与直线AB，CD相交.图中所示的各个角中，能看做∠1的内错角的是（）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
4. 下列等式中，从左到右的变形为因式分解的是（）

A、 $x + 2 y = (x + y) + y$ B、 $p (q + h) = p q + p h$ C、 $4 a^{2} - 4 a + 1 = 4 a (a - 1) + 1$ D、 $5 x^{2} y - 10 x y^{2} = 5 x y (x - 2 y)$

查看试题解析
5. 如图， $A B // C D$ ，点 $O$ 在 $A B$ 上， $O E$ 平分 $∠ B O D$ ，若 $∠ C D O = 100 °$ ，则 $∠ B O E$ 的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
6. 已知 $a = {(- 2)}^{0}$ ， $b = {(- 2)}^{- 1}$ ，则a与b的大小关系为（）

A、 $a > b$ B、 $a < b$ C、 $a = b$ D、 $a \geq b$

查看试题解析
7. 若 $x^{2} + k x + 64$ 为一个完全平方式，则 $k$ 的值为（）

A、16 B、 $\pm 16$ C、8 D、 $\pm 8$

查看试题解析
8. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+3b），宽为（a+2b）的大长方形，则需要A类、B类和C类卡片的张数分别为（）

A、 $2$ ， $8$ ， $5$ B、 $3$ ， $8$ ， $6$ C、 $3$ ， $7$ ， $5$ D、 $2$ ， $6$ ， $7$

查看试题解析
9. 若 $s + t = 4$ ，则 $s^{2} - t^{2} + 8 t$ 的值是（）

A、8 B、12 C、16 D、32

查看试题解析
10. 关于x，y的方程组为 ${\begin{array}{l} a x + 2 y = - 5 \\ - x + a y = 2 a \end{array}$ ，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当a每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，则这个公共解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 3 \end{array}$

查看试题解析

二、填空题

11. 计算： $16 y^{2} \div (8 y) =$ .

查看试题解析
12. 将4x−3y=5变形成含x的代数式表示y，则y=.

查看试题解析
13. 已知 ${\begin{array}{l} x = - 2 \\ y = a \end{array}$ 是方程 $2 x + 3 y = 5$ 的一个解，则a的值为.

查看试题解析
14. 因式分解： $a^{2} - 9 =$ ；
$a^{2} b - 6 a b + 9 b =$ .

查看试题解析
15. 如图，把一块三角板的 $60 °$ 角的顶点放在直尺的一边上，若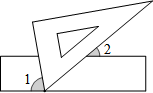 $∠ 1 = 3 ∠ 2 - 20 °$ ，则 $∠ 1 =$ $°$ .

查看试题解析
16. 有下列说法：
①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；
②无论k取任何实数，多项式 $x^{2} - k y^{2}$ 总能分解成两个一次因式积的形式；
③已知二元一次方程组 ${\begin{array}{l} x + y = 6 \\ a x + y = 4 \end{array}$ 的解也是二元一次方程 $x - 3 y = - 2$ 的解，则a的值是2；
④若 $x = 2^{m} + 1$ ， $y = 4^{m} - 3$ ，则 $y = x^{2} - 4$ ；
其中正确的说法是.

查看试题解析

三、解答题

17. 用代入消元法解二元一次方程组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 0 \\ x - y = 5 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x}{3} - \frac{y}{4} = 1 \\ 3 x - 4 y = 2 \end{array}$ .

查看试题解析
18.

(1)、先化简，再求值： $m (m - 2 n) + {(m + n)}^{2} - (m + n) (m - n)$ ，其中 $m = - 1$ ， $n = 4$ ；

(2)、已知 $x + y = 3$ ， $x y = 2$ ，求 ${(x - y)}^{2}$ 的值．

查看试题解析
19. 给出三个多项式：① $a^{2} + 3 a b - 2 b^{2}$ ， ② $b^{2} - 3 a b$ ， ③ $a b + 6 b^{2}$ .

(1)、请任意选择两个多项式进行加法运算，并把结果因式分解；

(2)、当 $a = 4$ ， $b = - 7$ 时，求第（1）问所得的代数式的值.

查看试题解析
20. 如图，已知 $∠ 1 = ∠ 2 = ∠ 3$ .

(1)、求证： $a / / b$

(2)、若 $∠ 1 = 55 °$ ，求 $∠ 4$ 的度数.

查看试题解析
21. 某公司计划印制一批宣传册.该宣传册每本共10页，由A、B两种彩页构成.已知A种彩页制版费300元/页，B种彩页制版费200元/页，共计2400元.（注：彩页制版费与印数无关）

(1)、求每本宣传册中A、B两种彩页各有多少页.

(2)、据了解，A种彩页印刷费2.5元/页，B种彩页印刷费1.5元/页，公司准备印制这批宣传册1500本，求印制这批宣传册制版费与印刷费的总和是多少元.

查看试题解析
22. 如图所示，有一块边长为(3a+b)米和(a+2b)米的长方形土地，现准备在这块土地上修建一个长为(2a+b)米，宽为(a+b)米的游泳池，剩余部分修建成休息区域.

(1)、请用含a和b的代数式表示休息区域的面积；（结果要化简）

(2)、若 $a = 5$ ， $b = 10$ ，求休息区域的面积；

(3)、若游泳池面积和休息区域的面积相等，且 $a \neq 0$ ，求此时游泳池的长与宽的比值.

查看试题解析
23. （1）问题发现：如图①，直线AB $∥$ CD，连接BE，CE，可以发现∠B+∠C=∠BEC.
请把下面的证明过程补充完整：
证明：过点E作EF $∥$ AB，
∵AB $∥$ DC（已知），EF $∥$ AB（辅助线的作法），
∴EF $∥$ DC（               ）.
∴∠C=∠CEF.（               ）
∵EF $∥$ AB，
∴∠B=∠BEF（同理），
∴∠B+∠C=      ▲      （等量代换）
即∠B+∠C=∠BEC.

(1)、拓展探究：如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C=360°−∠BEC.

(2)、解决问题
如图③，AB $∥$ DC，E、F、G是AB与CD之间的点，找出∠1，∠2，∠3，∠4，∠5之间的数量关系，并说明理由.

查看试题解析