2023年浙教版数学八年级下学期高分速效复习4 一元二次方程（进阶版）

试卷更新日期：2023-03-28 类型：复习试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列方程中，是关于x的一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ （a、b、c是实数） B、 $(x + 1) (x + 2) = {(x + 1)}^{2}$ C、 $x^{2} + \frac{1}{x} - 3 = 0$ D、 $2 x^{2} - 1 = 0$

查看试题解析
2. 已知1和2是关于x的一元二次方程ax²+bx+c＝0的两根，则关于x的方程a（x+1）²+b（x+1）+c＝0的根为（）

A、0和1 B、1和2 C、2和3 D、0和3

查看试题解析
3. 若关于x的一元二次方程 ( k-2)x²-2x+1=0有两个不相等的实数根，且k为非负整数，则符合条件的k的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边，a，b是关于x的方程x²－7x＋c＋7＝0的两根，那么AB边上的中线长是（　　）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、5 D、2

查看试题解析
5. 一个等腰的底边为4，腰是方程 $x^{2} - 5 x + 6 = 0$ 的一个根.则这个等腰三角形的周长可能是（）

A、8 B、10 C、8或10 D、9

查看试题解析
6. 已知方程 $x^{2} + 2019 x - 3 = 0$ 的两根分别是 $α$ 和 $β$ ，则代数式 $α^{2} + α β + 2019 α$ 的值为（）

A、1 B、0 C、2019 D、-2019

查看试题解析
7. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
②若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ 其中正确的（）

A、只有①②④ B、只有①②③ C、①②③④ D、只有①②

查看试题解析
8. 规定：如果关于x的一元二次方程ax²+bx+c＝0（a≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”现有下列结论
①方程x²+2x﹣8＝0是倍根方程；②若关于x的方程x²+ax+2＝0是倍根方程，则a＝±3；③若（x﹣3）（mx﹣n）＝0是倍根方程，则n＝6m或3n＝2m；④若点（m，n）在反比例函数y＝ $\frac{2}{x}$ 的图象上，则关于x的方程mx²﹣3x+n＝0是倍根方程.上述结论中正确的有（）

A、② B、①③ C、②③④ D、②④

查看试题解析
9. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400 $c m^{2}$ ，设金色纸边的宽度为xcm（风景画四周的金色纸边宽度相同），则x的值为（）

A、10 B、8 C、7 D、5

查看试题解析
10. 某市某鞋厂10月份的运动鞋产量为24万双，因销量较好，11月份、12月份均增大产量，使第四季度的总产量达到88万双设该厂11、12月份的运动鞋产量的月平均增长率为x，根据题意可列方程为（）

A、 $88 {(1 + x)}^{2} = 24$ B、 $88 {(1 - x)}^{2} = 24$ C、 $24 {(1 + x)}^{2} = 88$ D、 $24 + 24 (1 + x) + 24 {(1 + x)}^{2} = 88$

查看试题解析

二、填空题（每空3分，共18分）

11. 关于x的方程（1-m²）x²+2mx-1=0的所有根都是比1小的正实数，则实数m的取值范围是．

查看试题解析
12. 关于x的方程 $x^{2} - 2 x + m = p^{2}$ ，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为.

查看试题解析
13. 若关于x的方程(a+1)x²+(2a﹣3)x+a﹣2＝0有两个不相等的实根，且关于x的方程 $\frac{a x}{1 + x} - 1 = \frac{3}{x + 1}$ 的解为整数，则满足条件的所有整数a的和是．

查看试题解析
14. 对于一切不小于2的自然数n，关于x的一元二次方程x²﹣（n+2）x﹣2n²=0的两个根记作a_n ， b_n（n≥2）， $\frac{1}{(a_{2} - 2) (b_{2} - 2)} + \frac{1}{(a_{3} - 2) (b_{3} - 2)}$ $+ \dots +$ $\frac{1}{(a_{2020} - 2) (b_{2020} - 2)}$ = ．

查看试题解析
15. 某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售，销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元，则第二周每个旅游纪念品的销售价格为元.

查看试题解析
16. 阅读理解：对于 $x^{3} - (n^{2} + 1) x + n$ 这类特殊的代数式可以按下面的方法分解因式：
$x^{3} - (n^{2} + 1) x + n = x^{3} - n^{2} x - x + n = x (x^{2} - n^{2}) - (x - n) = x (x - n) (x + n) - (x - n) = (x - n) (x^{2} + n x - 1)$ 理解运用：如果 $x^{3} - (n^{2} + 1) x + n = 0$ ，那么 $(x - n) (x^{2} + n x - 1) = 0$ ，

即有 $x - n = 0$ 或 $x^{2} + n x - 1 = 0$ ，

因此，方程 $x - n = 0$ 和 $x^{2} + n x - 1 = 0$ 的所有解就是方程 $x^{3} - (n^{2} + 1) x + n = 0$ 的解.

解决问题：求方程 $x^{3} - 5 x + 2 = 0$ 的解为.

查看试题解析

三、计算题（共8分）

17. 解下列方程：

(1)、 $x^{2} + 4 x - 1 = 0$ ；

(2)、 $2 x^{2} - 7 x + 3 = 0$ ；

(3)、 $9 (x + 1)^{2} = (2 x - 5)^{2}$ ；

(4)、 $(x + 2)^{2} - 10 (x + 2) + 25 = 0$ ．

查看试题解析

四、解答题（共9题，共64分）

18. 关于 $x$ 的方程 $a x^{2} + 2 (a - 3) x + (a - 2) = 0$ ，至少有一个整数解，且 $a$ 是整数，求 $a$ 的值.

查看试题解析
19. 已知m ， n分别是关于x的一元二次方程ax²+bx+c＝a与ax²+bx+c＝b的一个根，且m＝n+1．

(1)、当m＝2，a＝﹣1时，求b与c的值；

(2)、用只含字母a ， n的代数式表示b；

(3)、当a＜0时，函数y＝ax²+bx+c满足b²﹣4ac＝a ， b+c≥2a ， n≤﹣ $\frac{1}{2}$ ，求a的取值范围．

查看试题解析
20. 已知 $x_{1}$ 、 $x_{2}$ 是关于x的一元二次方程 $x^{2} - (2 m + 4) x + m^{2} = 0$ 的两个实数根．

(1)、当 $m = 0$ 时，求方程的根；

(2)、若 $(x_{1} - 2) (x_{2} - 2) = 8$ ，求 $m$ 的值；

(3)、若等腰 $△ A B C$ 的腰长为9， $x_{1}$ 、 $x_{2}$ 恰好是 $△ A B C$ 另外两边的长，求这个等腰三角形的周长．

查看试题解析
21. 如图，在直角梯形 $A B C D$ 中， $A D ∥ B C$ ， $∠ C = 90 °$ ， $B C = 16$ ， $D C = 12$ ， $A D = 21$ ．动点 $P$ 从点 $D$ 出发，沿射线 $D A$ 的方向以每秒2个单位的速度运动，动点 $Q$ 从点 $C$ 出发，沿射线 $C B$ 的方向以每秒1个单位的速度向点 $B$ 运动，点 $P$ ， $Q$ 分别从点 $D$ ， $C$ 同时出发，当点 $P$ 运动到点 $A$ 时，点 $Q$ 随之停止运动．设运动的时间为 $t$ （秒），当 $t$ 为何值时，以 $B$ ， $P$ ， $Q$ 三点为顶点的三角形是等腰三角形？

查看试题解析
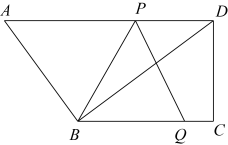22. 定义：若两个一元二次方程有且只有一个相同的实数根，我们就称这两个方程为“同伴方程”.例如x²=4和（x-2）（x+3）=0有且只有一个相同的实数根x=2，所以这两个方程为“同伴方程”.

(1)、根据所学定义，下列方程属于“同伴方程”的有：（只填写序号即可）
① ${(x - 1)}^{2} = 9$ ②x²+4x+4=0 ③ $x^{2} + 2 x - 8 = 0$

(2)、关于x的一元二次方程x²-2x=0与x²+x+m-1=0为“同伴方程”，求m的值；

(3)、若关于x的一元二次方程ax²+bx+c=0(a≠0)同时满足a-b+c=0和9a+3b+c=0，且与
（x-n）（x+3）=0互为“同伴方程”，求n的值.

查看试题解析
23. 定义：若关于x的一元二次方程 $a x^{2} + b x + c = 0$ $(a \neq 0)$ 的两个实数根为 $x_{1}$ ， $x_{2}$ $(x_{1} < x_{2})$ ，分别以 $x_{1}$ ， $x_{2}$ 为横坐标和纵坐标得到点 $M (x_{1} ， x_{2})$ ，则称点 $M$ 为该一元二次方程的衍生点．已知关于x的一元二次方程为 $x^{2} - 2 (m - 1) x + m^{2} - 2 m = 0$ ．

(1)、求证：不论m为何值，该方程总有两个不相等的实数根；

(2)、求衍生点M的轨迹的解析式；

(3)、若无论k $(k \neq 0)$ 为何值，关于x的方程 $a x^{2} + b x + c = 0$ 的衍生点M始终在直线 $y = k x - 2 (k - 2)$ 的图象上，求b与c满足的关系．

查看试题解析
24. 如图，在△ABC中，∠C=90°，AC=6 cm，BC=8 cm，点P从点A出发沿AC边向点C以1 cm/s的速度运动，同时点Q从点C出发沿CB边向点B以2 cm/s的速度运动.当点Q到达点B时，点P同时停止运动.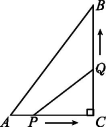

(1)、运动几秒时，△PCQ的面积为8 cm²?

(2)、△PCQ的面积能否等于△ABC面积的一半?若能，求出运动时间；若不能，请说明理由.

查看试题解析
25. 如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE＝ $\sqrt{2}$ c，这时我们把关于x的形如 $a x^{2} + \sqrt{2} c x + b = 0$ 的一元二次方程称为“勾系一元二次方程”.
请解决下列问题：

(1)、判断下列方程是否是“勾系一元二次方程”：
① $2 x^{2} + \sqrt{5} x + 1 = 0$ （填“是”或“不是”）；
② $3 x^{2} + 5 \sqrt{2} x + 4 = 0$ （填“是”或“不是”）

(2)、求证：关于x的“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 必有实数根；

(3)、若 $x = - 1$ 是“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 的一个根，且四边形ACDE的周长是12，求△ABC面积.

查看试题解析
26. 背景知识城镇化是指农村人口转化为城镇人口的过程，城镇化率是指一个地区城镇人口数占该地区人口总数的比例.问题解决：截止2016年底，某市人口总数约为400万人，城镇化率为 $m$ ；到2020年底，该市总人口增加了20万人，城镇人口增加了28万人，城镇化率达到 $(m + 4 %)$ .

(1)、求2016年该市的城镇化率 $m$ ；

(2)、2016年，该市城镇居民人均可支配收入为 $a$ 万元，农村居民人均可支配收入比城镇居民人均可支配收入少 $n a$ 万元；2020年，该市城镇居民人均可支配收入是2016年的1.5倍，农村居民人均可支配收入比2016年增长的百分率为n.这样，2020年全市居民人均可支配收入达到2016年全市居民人均可支配收入的1.5倍.
①用含 $a$ ， $n$ 的式子表示2016年全市居民的人均可支配收入；

②求 $n$ 的值.

查看试题解析