冲刺2023中考——数学模拟考场仿真演练卷九
试卷更新日期:2023-03-28 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 下列计算正确的是( )A、 B、 C、2 D、2. 中国共产主义青年团是中国青年的先锋队,是中国共产党的忠实助手和可靠后备军、截止至2021年12月31日,全国共有共青团员7371.5万名,将7371.5万用科学记数法表示为( )A、0.73715×108 B、7.3715×108 C、7.3715×107 D、73.715×1063. 将一个三角尺按如图所示的方式放置在一张平行四边形的纸片上,∠EFG=90°,∠EGF=60°,∠AEF=50°,则∠EGC的度数为( )
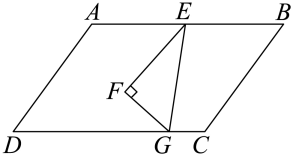 A、100° B、80° C、70° D、60°4. 如图,△ABC 与△DEF 位似,点 O 是它们的位似中心,且相似比为 1:2,则△ABC 与△DEF 的周长之比是( )
A、100° B、80° C、70° D、60°4. 如图,△ABC 与△DEF 位似,点 O 是它们的位似中心,且相似比为 1:2,则△ABC 与△DEF 的周长之比是( ) A、1:2 B、1:4 C、1:3 D、1:95. 学校连续三年组织学生参加义务植树,第一年共植树 400 棵,第三年共植树 625 棵.设该校植树棵数的年平均增长率为 x,根据题意,下列方程正确的是( )A、 B、 C、 D、6. 班长邀请 , , , 四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则 , 两位同学座位相邻的概率是( )
A、1:2 B、1:4 C、1:3 D、1:95. 学校连续三年组织学生参加义务植树,第一年共植树 400 棵,第三年共植树 625 棵.设该校植树棵数的年平均增长率为 x,根据题意,下列方程正确的是( )A、 B、 C、 D、6. 班长邀请 , , , 四位同学参加圆桌会议.如图,班长坐在⑤号座位,四位同学随机坐在①②③④四个座位,则 , 两位同学座位相邻的概率是( )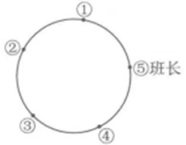 A、 B、 C、 D、7. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )
A、 B、 C、 D、7. 如图,在四边形材料中, , , , , .现用此材料截出一个面积最大的圆形模板,则此圆的半径是( )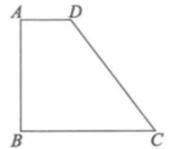 A、 B、8cm C、 D、10cm8. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
A、 B、8cm C、 D、10cm8. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )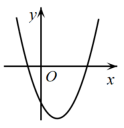 A、
A、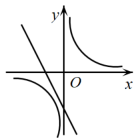 B、
B、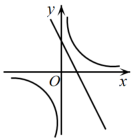 C、
C、 D、
D、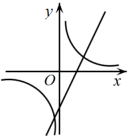 9. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、810. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )
9. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、810. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )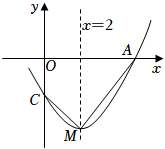 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每空3分,共18分)
-
11. 已知二元一次方程组 , 则的值为.12. 已知实数a、b满足a-b2=4,则代数式a2-3b2+a-14的最小值是 .13. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
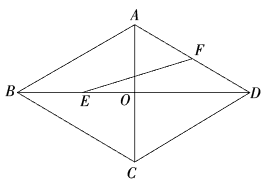 14. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .
14. 如图,在正方形中,E为的中点,连接交于点F.若 , 则的面积为 .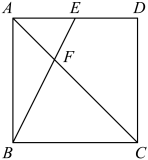 15. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .
15. 如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1=和y2=分别经过点B、点E,若S△COD=5,则k1﹣k2= .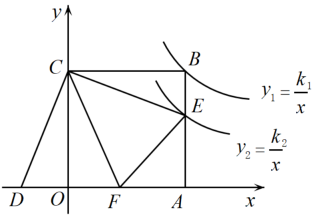 16. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
16. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.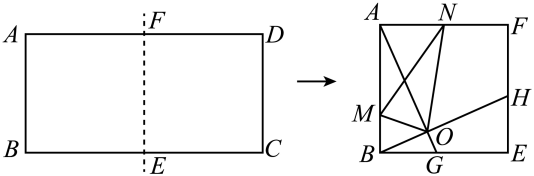
三、解答题(共9题,共72分)
-
17. 计算: .18. 先化简,再求值: , 从-3,-1,2中选择合适的a的值代入求值.19. 为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间t(单位:小时)划分为A:t<2,B:2≤t<3,C:3≤t<4,D:t≥4四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
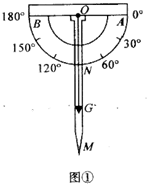
 (1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.20. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
(1)、这次抽样调查共抽取人,条形统计图中的m=;(2)、在扇形统计图中,求B组所在扇形圆心角的度数,并将条形统计图补充完整;(3)、已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?(4)、学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.20. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
 (2)、实地测量
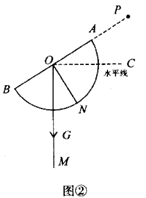
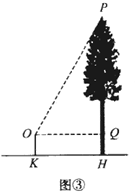
(2)、实地测量如图③,公园广场上有一棵树,为了测量树高,同学们在观测点 处测得顶端 的仰角 ,观测点与树的距离 为5米,点 到地面的距离 为1.5米;求树高 . ( ,结果精确到0.1米)
 (3)、拓展探究
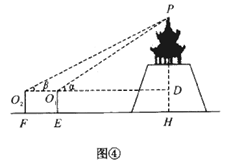
(3)、拓展探究公园高台上有一凉亭,为测量凉亭顶端 距离地面高度 (如图④),同学们讨论,决定先在水平地面上选取观测点 ( 在同一直线上),分别测得点 的仰角 ,再测得 间的距离 ,点 到地面的距离 均为1.5米;求 (用 表示).
 21. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 .
21. 如图,在中, , , 是边上的一点,以为直角边作等腰 , 其中 , 连接 . (1)、求证:;(2)、若时,求的长.22. 图,在中, , 点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.
(1)、求证:;(2)、若时,求的长.22. 图,在中, , 点D是边的中点,点O在边上,⊙经过点C且与边相切于点E,.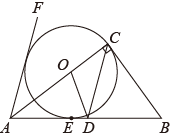 (1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径及的长.23. 如图,一次函数 与反比例函数 的图象相交于小 ,B两点,分别连接 , .
(1)、求证:是⊙的切线;(2)、若 , , 求⊙的半径及的长.23. 如图,一次函数 与反比例函数 的图象相交于小 ,B两点,分别连接 , .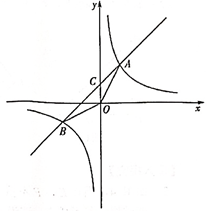 (1)、求这个反比例函数的表达式;(2)、求 的面积:(3)、在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.24. 如图
(1)、求这个反比例函数的表达式;(2)、求 的面积:(3)、在平面内是否存在一点P,使以点O,B,A,P为顶点的四边形为平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.24. 如图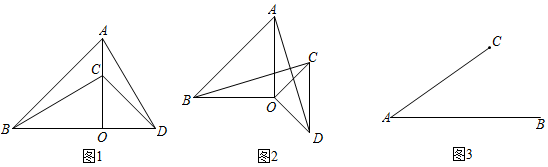 (1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,
(1)、如图1,和是等腰直角三角形, , 点C在OA上,点D在线段BO延长线上,连接AD,BC.线段AD与BC的数量关系为;(2)、如图2,将图1中的绕点O顺时针旋转()第一问的结论是否仍然成立;如果成立,证明你的结论,若不成立,说明理由.(3)、如图,若 , 点C是线段AB外一动点, , 连接BC,①若将CB绕点C逆时针旋转90°得到CD,连接AD,则AD的最大值 ▲ ;
②若以BC为斜边作 , (B、C、D三点按顺时针排列), , 连接AD,当时,直接写出AD的值.
25. 如图,抛物线经过 , 两点,与x轴的另一个交点为A,与y轴相交于点C. (1)、求抛物线的解析式和点C的坐标;(2)、若点M在直线上方的抛物线上运动(与点B,C不重合),求使面积最大时M点的坐标,并求最大面积;(请在图1中探索)(3)、设点Q在y轴上,点P在抛物线上,要使以点A,B,P,Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)
(1)、求抛物线的解析式和点C的坐标;(2)、若点M在直线上方的抛物线上运动(与点B,C不重合),求使面积最大时M点的坐标,并求最大面积;(请在图1中探索)(3)、设点Q在y轴上,点P在抛物线上,要使以点A,B,P,Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)