浙江省杭州市余杭区联盟校2022-2023学年七年级下学期3月份独立作业数学试题

试卷更新日期：2023-03-28 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图，属于同位角是（）

A、∠1和∠2 B、∠1和∠3 C、∠1和∠4 D、∠2和∠3

查看试题解析
2. 如图，已知 $∠ B = ∠ A E F$ ，则（）

A、 $E F ∥ B C$ B、 $A D ∥ E F$ C、 $A D ∥ B C$ D、 $A B ∥ C D$

查看试题解析
3. 已知“x与y的差的2倍等于9”，则可列方程（）

A、 $x - y = 9 \times 2$ B、 $x - 2 y = 9$ C、 $2 x - y = 9$ D、 $2 (x - y) = 9 .$

查看试题解析
4. 如图，将 $△ A B C$ 沿射线 $B C$ 平移得到 $△ D E F$ ，则下列线段的长度中表示平移距离的是（）

A、 $B C$ B、 $B F$ C、 $B E$ D、 $C E$

查看试题解析
5. 一辆汽车向前行驶，两次拐弯后，仍在原来的方向上前行，以下可能的情况是（）

A、先右拐50°，后左拐130° B、先左拐50°，后右拐50° C、先左拐50°，后左拐130° D、先右拐50°，后右拐50°

查看试题解析
6. 如图，三角板的直角顶点在直尺的一边上.若 $∠ 1 = 30 °$ ， $∠ 2 = 70 °$ ，则 $∠ 3$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
7. 已知 ${\begin{array}{l} x = 1 ， \\ y = - 2 \end{array}$ 是关于x，y的二元一次方程 $a x + y = 1$ 的一个解，那么a的值为（）

A、3 B、1 C、-1 D、-3

查看试题解析
8. 如图， $l_{1} ∥ l_{2}$ ，则（）

A、 $∠ α + ∠ β - ∠ γ = 180 °$ B、 $∠ α + ∠ β + ∠ γ = 180 °$ C、 $∠ α + ∠ β = 2 ∠ γ$ D、 $∠ α + ∠ β = ∠ γ$

查看试题解析
9. 如图，将7张相同的长方形纸片不重叠的放在长方形 $A B C D$ 内，已知小长方形纸片的长为a，宽为b，且 $a > b$ ，若未被覆盖的两个长方形周长相等，则（）

A、 $a = \frac{5}{2} b$ B、 $a = 3 b$ C、 $a = \frac{7}{2} b$ D、 $a = 4 b$

查看试题解析
10. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{matrix} x + 2 y = a - 3 \\ 3 x - y = 2 a \end{matrix}$ ，有下列说法：①当 $a = 2$ 时，方程的两根互为相反数；②不存在自然数 $a$ ，使得 $x$ ， $y$ 均为正整数；③ $x$ ， $y$ 满足关系式 $x - 5 y = 6$ ；④当且仅当 $a = - 5$ 时，解得 $x$ 为 $y$ 的2倍．其中正确的是（）

A、①②③④ B、①③④ C、②③ D、①②④

查看试题解析

二、填空题

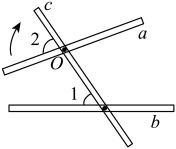
11. 如图表示钉在一起的木条a，b，c.若测得 $∠ 1 = 50 ° ， ∠ 2 = 75 °$ ，要使木条 $a ∥ b$ ，木条a至少要旋转°.

查看试题解析
12. 已知二元一次方程3x－2y＝10，用含x的代数式表示y，则y＝．

查看试题解析
13. 若关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + 2 y = 4 k \\ x - y = k \end{array}$ 的解也是 $2 x + y = 10$ 的解，则 $k$ 的值为.

查看试题解析
14. 如图，直线 $l_{1} ∥ l_{2}$ ， $A Q$ 平分 $∠ D A C$ ， $∠ 1 = 50 °$ ， $∠ 2 = 25 °$ ，则 $∠ 3 =$ °.

查看试题解析
15. 已知方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解是 ${\begin{array}{l} x = 4 \\ y = 10 \end{array}$ ，则方程组 ${\begin{array}{l} 4 a_{1} x + 5 b_{1} y = 9 c_{1} \\ 4 a_{2} x + 5 b_{2} y = 9 c_{2} \end{array}$ 的解是.

查看试题解析
16. 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB，CD，

(1)、如图1，若BE∥CG，∠1=55°，则∠2的度数是.

(2)、如图2，若CD∥BE，且 $∠ 3 = 50 °$ ，则 $∠$ 4的度数是.

查看试题解析

三、解答题

17. 如图1，数学课上，老师在黑板上画出两条直线 $a$ ， $b$ ，两条直线所成的角跑到黑板外面去了.老师让小明在黑板上测量出直线 $a$ ， $b$ 所成的角的度数，他该怎么办？请在图2中画出测量示意图，简要说明画图方法和理由.

查看试题解析
18. 用指定的方法解下列方程组

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{array}$ （代入法）

(2)、 ${\begin{array}{l} 3 x + 4 y = 16 \\ 5 x - 6 y = 33 \end{array}$ （加减法）

查看试题解析
19. 如图是潜望镜示意图， $A B ， C D$ 代表镜子.且 $A B ∥ C D$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ .求证： $M N ∥ E F$ .
请补全下述证明过程：
证明：∵ $A B ∥ C D$ ，
∴ $∠ 2 =$       ▲      .
∵ $∠ 1 = ∠ 2 ， ∠ 3 = ∠ 4$ ，
∴ $∠ 1 = ∠ 2 = ∠ 3 = ∠ 4$ .
∵ $∠ 1 ＋ ∠ 2 ＋ ∠ 5 = 180 °$ ，
$∠ 3 ＋ ∠ 4 ＋$       ▲       $= 180 °$ ，
∴ $∠ 5 =$       ▲      .
∴ $M N ∥ E F$ （    ）.

查看试题解析
20. 如图，已知AB∥CD，
∠1=∠2. 求证：∠E=∠F.

查看试题解析
21. 若方程组 ${\begin{array}{l} 3 x - y = 7 \\ a x + y = b \end{array}$ 和方程组 ${\begin{array}{l} x + b y = a \\ 2 x + y = 8 \end{array}$ 有相同的解，求a，b的值.

查看试题解析
22. 已知，某医用材料厂商有甲、乙两条口罩生产线，在原有产能下，每天甲生产线比乙生产线少生产56万只，两条生产线3天共生产口罩336万只．

(1)、在原有产能下，求甲、乙两条生产线每天各生产口罩多少万只？

(2)、该厂家收到订单，需要生产840万只口罩，两条生产线同时工作了2天后，该厂家加快了生产速度，又用5天时间完成了全部订单，求提升产能后，该厂家的日产量增加了多少万只？

查看试题解析
23. 如图1，直线 $A B$ 与直线 $l_{1}$ ， $l_{2}$ 分别交于C，D两点，点M在直线 $l_{2}$ 上，射线 $D E$ 平分 $∠ A D M$ 交直线 $l_{1}$ 于点Q， $∠ A C Q = 2 ∠ C D Q$ .

(1)、求证 $l_{1} ∥ l_{2}$ .

(2)、如图2，射线 $Q P$ 交直线 $l_{2}$ 于点F，交线段 $C D$ 于点P，且 $∠ A C Q = 70 °$ .
①若 $∠ Q F D = 20 °$ ，直接写出 $∠ F Q D$ 的度数.
②点N在射线 $D E$ 上，满足 $∠ Q C N = ∠ Q F D$ ，连接 $C N$ ，请补全图形，探究 $∠ C N D$ 与 $∠ F Q D$ 满足的等量关系，并说明理由.

查看试题解析