江苏省宿迁市沭阳县2022-2023学年九年级下学期第五次学情调研数学试题

试卷更新日期：2023-03-28 类型：月考试卷

进入出卷网下载

一、单选题

1. 方程 $x (x - 1) = 0$ 的根是（）

A、 $x = 0$ B、 $x = 1$ C、 $x_{1} = 0 ， x_{2} = 1$ D、 $x_{1} = 1 ， x_{2} = - 1$

查看试题解析
2. 已知⊙O的半径为4cm，点P到圆心O的距离为3cm，则点P（）

A、在圆内 B、在圆上 C、在圆外 D、不能确定

查看试题解析
3. 某班有6个学习小组，每组的人数分别为3，4，5，6，6，7，这组数据的中位数是（）

A、4 B、5 C、5.5 D、6

查看试题解析
4. 如图，在 $△ A B C$ 中，点D，E分别为 $A B ， A C$ 的中点，若 $D E = 2$ ，则 $B C$ 的长度为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 二次函数 $y = x^{2} - 2 x$ 的顶点坐标是（）

A、 $(1, 1)$ B、 $(1, - 1)$ C、 $(- 1, - 1)$ D、 $(- 1, 1)$

查看试题解析
6. 如图，四边形 $A B C D$ 为 $⊙ O$ 的内接四边形，若 $∠ A B C = 125 °$ ，则 $∠ A O C$ 等于（）

A、 $55 °$ B、 $110 °$ C、 $105 °$ D、 $125 °$

查看试题解析
7. 若关于x的一元二次方程 $x^{2} + 2 x - (k - 1) = 0$ 有实数根，则k的取值范围是（）

A、 $k > 0$ B、 $k \geq 0$ C、 $k < 0$ D、 $k \leq 0$

查看试题解析
8. 如图，在6×6的正方形网格图形 $A B C D$ 中，M，N分别是 $A B ， B C$ 上的格点， $B M = 4 ， B N = 2$ .若点P是这个网格图形中的格点，连接PM，PN，则所有满足 $∠ M P N = 45 °$ 的 $△ P M N$ 中， $D P$ 的最小值是（）

A、 $3 \sqrt{2} - \sqrt{10}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

9. 若 $\frac{a}{4} = \frac{b}{3}$ ，则 $\frac{b}{a - b} =$ .

查看试题解析
10. 抛掷一枚质地均匀的正方体骰子一次，骰子的六个面上分别刻有1到6的点数，观察向上的一面，点数为6的事件的概率是.

查看试题解析
11. 2022年世界杯小组赛于12月4日结束，B组、F组两组四个球队3场比赛积分数据如图所示，则积分较整齐的小组是.（填“B”或“F”）.

查看试题解析
12. 一个圆锥的母线长为5cm，底面圆半径为3cm，则这个圆锥的侧面积是 $c m^{2}$ （结果保留 $π$ ）.

查看试题解析
13. 已知m是方程 $x^{2} + 2 x - 1 = 0$ 的一个根，则代数式 $2 m^{2} + 4 m + 2021$ 的值为

查看试题解析
14. 若抛物线 $y = - x^{2} + 2 x - 2$ ，点 $(- 2 ， y_{1}) ， (3 ， y_{2})$ 为抛物线上两点，则 $y_{1}$ $y_{2}$ .（用“ $<$ ”或“ $>$ ”号连接）

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ A C D = ∠ B ， A D = 2 ， B D = 6$ ，则 $A C =$ .

查看试题解析
16. 已知二次函数 $y = (x - m)^{2} + n$ 的图像与x轴交于点 $(- 1 ， 0) ， (3 ， 0)$ ，则关于x的一元二次方程 $(x - m + 2)^{2} + n = 0$ 的解为.

查看试题解析
17. 如图，在正方形网格中， $⊙ O$ 的内接 $△ A B C$ 的顶点均为格点，则 $t a n A$ 的值为.

查看试题解析
18. 如图，二次函数 $y = a x^{2} + 2 a x - 3 a$ 与x轴交于点A，B，对称轴为直线l，顶点C到x轴的距离为 $2 \sqrt{3}$ .点P为直线l上一动点，另一点从C出发，先以每秒2个单位长度的速度沿 $C P$ 运动到点P，再以每秒1个单位长度的速度沿 $P A$ 运动到点A停止，则时间最短为秒.

查看试题解析

三、解答题

19. 计算： $\tan 45 ° - \sin 30 ° \cos 60 ° - \cos^{2} 45 °$

查看试题解析
20. 解方程： $x^{2} + 2 x - 15 = 0$

查看试题解析
21. 如图，已知在 $△ A B C$ 中， $∠ A = 90 °$ .

(1)、请用圆规和直尺作出 $⊙ P$ ，使圆心P在边 $A C$ 上，且与边 $A B$ ， $B C$ 都相切（保留作图痕迹，不写作法和证明）.

(2)、若 $∠ B = 60 ° ， A C = 3$ ，则 $⊙ P$ 的周长为.（结果保留 $π$ ）

查看试题解析
22. 某校开展了“文明城市”活动周，活动周设置了“A：文明礼仪，B：生态环境，C：交通安全，D：卫生保洁”四个主题活动，每个学生限选一个主题参与.为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.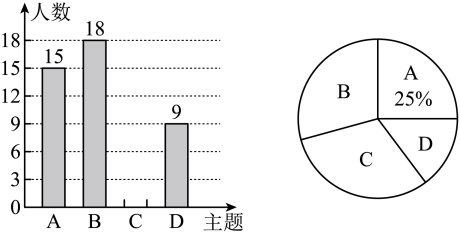

(1)、本次随机调查的学生人数是人；

(2)、补全条形统计图；

(3)、在扇形统计图中，“B”主题对应扇形的圆心角为度；

(4)、若该校共有 $1800$ 名学生，试估计该校参与“生态环境”主题的学生人数.

查看试题解析
23. 近期国内疫情形势持续变化，为守护好个人身体健康，广大市民应尽快完成新冠疫苗接种.为了继续宣传新冠疫苗接种的重要性，某小区管理部门准备在已经接种疫苗的居民中征集志愿宣传者，现有2男2女共4名居民报名.

(1)、随机抽取1人，恰好是男性的概率为；

(2)、随机抽取2人，求恰好抽到一男和一女的概率.

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径，C是 $⊙ O$ 上一点，P是 $A B$ 的延长线上一点，且 $∠ P C B = ∠ A$ .

(1)、判断直线 $P C$ 与 $⊙ O$ 的位置关系，并说明理由；

(2)、若 $⊙ O$ 的半径为3， $B P = O B$ ，求图中阴影部分的面积.

查看试题解析
25. 如图①中 $N 、 A 、 M 、 C$ 共线，若 $A B = 4$ 米， $∠ M A B$ 的范围： $30 ° \leq ∠ M A B \leq 60 ° ， ∠ A B C$ 的范围： $45 ° \leq ∠ A B C \leq 105 °$ .

(1)、如图②，当 $∠ M A B = 45 °$ ， BC恰好垂直 $M N$ 时，求 $B C$ 的长；（结果保留根号）

(2)、若（1）中 $B C$ 长度不变，求点 $C 、 A$ 间最远的距离多少米.（结果保留根号）

查看试题解析
26. 宿迁市桃树栽培历史悠久，素有“夭桃千顷、翠柳万行”的美誉.小李家有一片80棵桃树的桃园，现准备多种一些桃树提高桃园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低.若该桃园每棵桃树产桃y（千克）与增种桃树x（棵）之间的函数关系如图所示.

(1)、求y与x之间的函数关系式；

(2)、当桃园总产量为7000千克时，求x的值；

(3)、如果增种的桃树x（棵）满足： $10 \leq x \leq 50$ ，请你写出桃园的总产量W（千克）与x之间的函数关系式，并帮小李计算，桃园的总产量最多是多少千克？

查看试题解析
27. 如图
如图①，已知矩形 $A B C D$ ， $A B = 6 ， A D = 8$ .点E从点B出发，沿边 $B C$ 运动至点C停止.以 $D E$ 为直径作 $⊙ O$ ， $⊙ O$ 与对角线 $A C$ 交于点F，连接 $F D$ ， $F E$ .

(1)、如图②，当E运动至终点C时，求 $\frac{F D}{F E}$ 的值；

(2)、试探究：在点E运动的过程中， $\frac{F D}{F E}$ 的值是否为定值？若是，请求出这个值；若不是，请说明理由；

(3)、如图③，以 $F D$ ， $F E$ 为边构造矩形 $D F E G$ ，连接 $C G$ ，求证： $△ A D F ∽ △ C D G$ ，并直接写出在这一运动过程中，点G所经过的路径长.

查看试题解析
28. 定义：函数图象上到两坐标轴的距离都不大于 $n (n \geq 0)$ 的点叫做这个函数图象的“n阶方点”.例如，点 $(1 ， 1)$ 是一次函数 $y = x$ 图像的“1阶方点”.

(1)、在① $(1 ， 1)$ ， ② $(- 2 ， - \frac{1}{2})$ ， ③ $(- \frac{5}{2} ， - \frac{2}{5})$ 三点中，是反比例函数 $y = \frac{1}{x}$ 图像的“2阶方点”的有（填序号）；

(2)、如图，已知抛物线 $y = - (x + 1)^{2} + 4$ 交y轴于点C，一次函数 $y = a x + 2 a + 3$ 的图像交抛物线第二象限于点P，点Q为该一次函数图象的“1阶方点”.
①求 $△ P C Q$ 的面积的最大值；
②若一次函数 $y = a x + 2 a + 3$ 图像的“1阶方点”有且只有一个，求a的值；

(3)、若抛物线 $y = - (x - m)^{2} - 2 m + 2$ 的“m阶方点”一定存在，求m的取值范围.

查看试题解析