浙江省金华市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-03-28 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示，直线a，b相交于点O，若∠1等于50°，则∠2等于（）

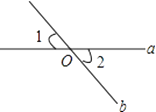A、50° B、40° C、140° D、130°

查看试题解析
2. 如图，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（）的长.

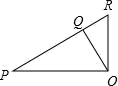A、OQ B、OR C、OP D、PQ

查看试题解析
3. 下列图形中，能由∠1＝∠2得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，已知AC∥BD，∠CAE=30°，∠DBE=45°，则∠AEB等于（）

A、30° B、45° C、60° D、75°

查看试题解析
5. 将如图所示的图案通过平移后可以得到的图案是（）

A、 B、 C、 D、

查看试题解析
6. 以下四个说法：①负数没有平方根；②一个正数一定有两个平方根；③平方根等于它本身的数是0和1；④一个数的立方根不是正数就是负数.其中正确的说法有（）.

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 在实数 $\frac{22}{7}$ ，－ $\sqrt{2}$ ， $\sqrt[3]{9}$ ， $- 3.14159$ ，－ $\sqrt{64}$ ， $0$ ， $\frac{π}{2}$ ， $\sqrt[3]{- 64}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 在平面直角坐标系中，将点P（﹣2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P′的坐标是（）

A、（2，4） B、（1，5） C、（1，-3） D、（-5，5）

查看试题解析
10. 如图1是一局围棋比赛的几手棋.为记录棋谱方便，横线用数字表示，纵线用字母表示，这样，黑棋的位置可记为（B，2），白棋②的位置可记为(D，1)，则白棋⑨的位置应记为（）

A、（C，5） B、(C，4) C、(4，C) D、(5，C)

查看试题解析

二、填空题

11. 已知 $a 、 b$ 为两个连续的整数，且 $a < \sqrt{11} < b$ ，则 $a + b$ = .

查看试题解析
12. 若 $\sqrt{3}$ 的整数部分是a，小数部分是b，则 $\sqrt{3} a - b$ = ．

查看试题解析
13. 将一条2cm长的斜线段向右平移3cm后，连接对应点得到的图形的周长是 cm．

查看试题解析
14. 如图，∠1=∠2，需增加条件可以使得AB∥CD（只写一种）．

查看试题解析
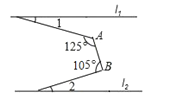
15.
如图，直线l₁∥l₂ ， ∠A=125°，∠B=105°，则∠1+∠2= °．

查看试题解析
16. 如图，一个机器人从点O出发，向正西方向走2m到达点A₁；再向正北方向走4m到达点A₂；再向正东方向走6m到达点A₃；再向正南方向走8m到达点A₄；再向正西方向走10m到达点A₅；…，按如此规律走下去，当机器人走到点A₂₀₁₇时，点A₂₀₁₇的坐标为．

查看试题解析

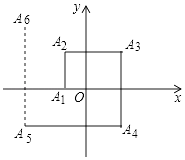
三、解答题

17. 已知xⁿ=2，yⁿ=3，求（x²y）²ⁿ的值．

查看试题解析
18. 先化简，再求值： $(x + 1) (x - 1) + x (2 - x) + {(x - 1)}^{2}$ ，其中 $x = 100$

查看试题解析
19. 若方程组 ${\begin{array}{l} 3 x - y = 7 \\ a x + y = b \end{array}$ 和方程组 ${\begin{array}{l} x + b y = a \\ 2 x - y = 8 \end{array}$ 有相同的解，求a，b的值．

查看试题解析
20. 如图，方格纸中每个小方格都是边长为1个单位长度的正方形，已知三角形ABC的顶点在格点上，在建立平面直角坐标系后，A的坐标为(2，－4)，B的坐标为(5，－4)，C的坐标为(4，－1).

（ 1 ）画出三角形ABC；

（ 2 ）求三角形ABC的面积；

（ 3 ）若把三角形ABC向上平移2个单位长度，再向左平移4个单位长度得到三角形A′B′C′，在图中画出三角A′B′C′，并写出B′的坐标.

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ D = 100 °$ ， CA平分 $∠ B C D$ ，且 $∠ A C B = 40 °$ ， $∠ B A C = 70 °$ .

(1)、 $A D$ 与 $B C$ 平行吗？请写出推理过程.

(2)、若点E在线段 $B A$ 的延长线上，求 $∠ D A C$ 与 $∠ E A D$ 的度数.

查看试题解析
22. 我们知道 $\sqrt{2}$ 是无理数，其整数部分是1，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分.请解答下列问题：

(1)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求 $a + b - \sqrt{5}$ 的值；

(2)、已知 $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x - y$ 的值.

查看试题解析
23. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足 $\sqrt{a - 4} + | b - 6 | = 0$ ，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.

(1)、a= ， b= ，点B的坐标为；

(2)、当点P移动4秒时，请指出点P的位置，并求出点P的坐标；

(3)、在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间.

查看试题解析