辽宁省锦州市2022-2023学年九年级下学期质量调查数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 下列命题:①同旁内角互补;②对顶角相等;③一个角的补角大于这个角;④三角形的一个外角等于两个内角之和,其中,真命题的个数是( )A、0个 B、1个 C、2个 D、3个2. 将 用小数表示为( )A、0.000205 B、0.0205 C、0.00205 D、-0.002053. 用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,它最少和最多需要的立方块是个.( )
 A、8与14 B、9与13 C、10与12 D、无法确定4. 对甲、乙两户居民家庭全年各项支出的统计如图所示,已知甲户居民的衣着支出与乙户相同.下面根据统计,对两户家庭教育支出的费用作出判断,正确的是( )
A、8与14 B、9与13 C、10与12 D、无法确定4. 对甲、乙两户居民家庭全年各项支出的统计如图所示,已知甲户居民的衣着支出与乙户相同.下面根据统计,对两户家庭教育支出的费用作出判断,正确的是( ) A、甲比乙大 B、乙比甲大 C、甲、乙一样大 D、无法确定5. 如图,AB DE,BC⊥CD,则以下说法中正确的是( )
A、甲比乙大 B、乙比甲大 C、甲、乙一样大 D、无法确定5. 如图,AB DE,BC⊥CD,则以下说法中正确的是( ) A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小6. 已知m,n均为正整数且满足 , 则的最小值是( )A、20 B、30 C、32 D、377. 已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M
A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小6. 已知m,n均为正整数且满足 , 则的最小值是( )A、20 B、30 C、32 D、377. 已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A、 B、 C、 D、8. 如图,在四边形ABCD中,AB∥CD,∠C=90°,AB=8,AD=CD=5,点M为BC上异于B,C的一定点,点N为AB上的一动点,E,F分别为DM、MN的中点,当N从A到B的运动过程中,线段EF扫过图形的面积为( ) A、4 B、4.5 C、5 D、6
A、4 B、4.5 C、5 D、6二、填空题
-
9. 要使式子有意义,则a的取值范围是 .10. 如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是.
 11. 对于三个数 , 我们规定用表示这三个数的平均数,用示这三个数中最小的数.例如: , , 如果 , 那么x=.12. 已知下面三个关于x的一元二次方程ax2+bx+c=1,bx2+cx+a=-3,cx2+ax+b=2恰好有一个相同的实数根,则a+b+c的值为 .13. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
11. 对于三个数 , 我们规定用表示这三个数的平均数,用示这三个数中最小的数.例如: , , 如果 , 那么x=.12. 已知下面三个关于x的一元二次方程ax2+bx+c=1,bx2+cx+a=-3,cx2+ax+b=2恰好有一个相同的实数根,则a+b+c的值为 .13. 如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .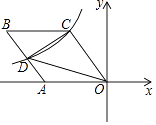 14. 如图所示,在扇形 中, ,半径 ,点 位于 的 处且靠近点 的位置.点 、 分别在线段 、 上, , 为 的中点,连接 、 .在 滑动过程中( 长度始终保持不变),当 取最小值时,阴影部分的周长为.
14. 如图所示,在扇形 中, ,半径 ,点 位于 的 处且靠近点 的位置.点 、 分别在线段 、 上, , 为 的中点,连接 、 .在 滑动过程中( 长度始终保持不变),当 取最小值时,阴影部分的周长为. 15. 如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作 于点E, 于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:① ;② ;③ ;④EF的最小值是 .其中正确的是 . (把你认为正确结论的序号都填上)
15. 如图,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作 于点E, 于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论:① ;② ;③ ;④EF的最小值是 .其中正确的是 . (把你认为正确结论的序号都填上) 16. 如图,已知等边△OA1B1 , 顶点A1在双曲线y= (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2 , 过A2作A2B2∥A1B1交x轴于点B2 , 得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3 , 过A3作A3B3∥A2B2交x轴于点B3 , 得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为 .
16. 如图,已知等边△OA1B1 , 顶点A1在双曲线y= (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2 , 过A2作A2B2∥A1B1交x轴于点B2 , 得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3 , 过A3作A3B3∥A2B2交x轴于点B3 , 得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为 .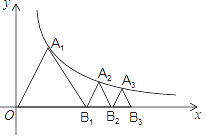
三、解答题
-
17. 先化简 , 然后从 的范围内选取一个合适的整数作为a的值代入求值.18. 荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
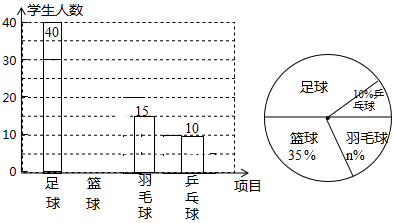 (1)、m= , n=;(2)、请补全上图中的条形图;(3)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;(4)、在抽查的m名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人.求小红、小梅能分在同一组的概率.19. 端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.(1)、请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;(2)、在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数向上代表肉馅,点数向上代表香肠馅,点数 , 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.
(1)、m= , n=;(2)、请补全上图中的条形图;(3)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;(4)、在抽查的m名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人.求小红、小梅能分在同一组的概率.19. 端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.(1)、请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;(2)、在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数向上代表肉馅,点数向上代表香肠馅,点数 , 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由. 20. 某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.(1)、求中巴车和大客车各有多少个座位?(2)、客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?21. 如图,在坡角为的山坡上有一铁塔 , 其正前方矗立着一大型广告牌,当阳光与水平线成角时,测得铁塔落在斜坡上的影子的长为8米,落在广告牌上的影子的长为5米,求铁塔AB的高.(、均与水平面垂直,结果保留根号)
20. 某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.(1)、求中巴车和大客车各有多少个座位?(2)、客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?21. 如图,在坡角为的山坡上有一铁塔 , 其正前方矗立着一大型广告牌,当阳光与水平线成角时,测得铁塔落在斜坡上的影子的长为8米,落在广告牌上的影子的长为5米,求铁塔AB的高.(、均与水平面垂直,结果保留根号) 22. 如图,已知点D是外接圆上的一点,于G,连接AD,过点B作直线交AC于E,交于F,若点F是弧CD的中点,连接OG,OD,CD.
22. 如图,已知点D是外接圆上的一点,于G,连接AD,过点B作直线交AC于E,交于F,若点F是弧CD的中点,连接OG,OD,CD.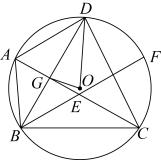 (1)、求证:;(2)、若 , 试探究与之间的数量关系,并证明.23. 为鼓励大学生毕业后自主创业,我市出台了相关政策:由政府协调,本市企业按成本价提供产品给应届毕业生自主销售,成本价与出厂价之间的差价由政府承担.赵某按照相关政策投资销售本市生产的一种新型“儿童玩具枪”.已知这种“儿童玩具枪”的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=−10x+500.(1)、赵某在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设赵某获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种“儿童玩具枪”的销售单价不得高于28元.如果赵某想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?24. 如图,在正方形 中, 是对角线 上的一个动点 ,连接 ,过点 作 交 于点 .
(1)、求证:;(2)、若 , 试探究与之间的数量关系,并证明.23. 为鼓励大学生毕业后自主创业,我市出台了相关政策:由政府协调,本市企业按成本价提供产品给应届毕业生自主销售,成本价与出厂价之间的差价由政府承担.赵某按照相关政策投资销售本市生产的一种新型“儿童玩具枪”.已知这种“儿童玩具枪”的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=−10x+500.(1)、赵某在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)、设赵某获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?(3)、物价部门规定,这种“儿童玩具枪”的销售单价不得高于28元.如果赵某想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?24. 如图,在正方形 中, 是对角线 上的一个动点 ,连接 ,过点 作 交 于点 . (1)、如图①,求证: ;(2)、如图②,连接 为 的中点, 的延长线交边 于点 ,当 时,求 和 的长;(3)、如图③,过点 作 于 ,当 时,求 的面积.25. 如图1,已知抛物线y=-x2-4x+5交x轴于点A、B两点(点A在点B的左侧),交y轴于点C,点D为抛物线的顶点,连接AD.
(1)、如图①,求证: ;(2)、如图②,连接 为 的中点, 的延长线交边 于点 ,当 时,求 和 的长;(3)、如图③,过点 作 于 ,当 时,求 的面积.25. 如图1,已知抛物线y=-x2-4x+5交x轴于点A、B两点(点A在点B的左侧),交y轴于点C,点D为抛物线的顶点,连接AD. (1)、求直线AD的解析式.(2)、点E(m,0)、F(m+1,0)为x轴上两点,其中(-5<m<-3.5)EE′、FF′分别平行于y轴,交抛物线于点E′和F′,交AD于点M、N,当ME′+NF′的值最大时,在y轴上找一点R,使得|RE′-RF′|值最大,请求出点R的坐标及|RE′-RF′|的最大值.(3)、如图2,在抛物线上是否存在点P,使得△PAC是以AC为底边的等腰三角形,若存在,请出点P的坐标及△PAC的面积,若不存在,请说明理由.
(1)、求直线AD的解析式.(2)、点E(m,0)、F(m+1,0)为x轴上两点,其中(-5<m<-3.5)EE′、FF′分别平行于y轴,交抛物线于点E′和F′,交AD于点M、N,当ME′+NF′的值最大时,在y轴上找一点R,使得|RE′-RF′|值最大,请求出点R的坐标及|RE′-RF′|的最大值.(3)、如图2,在抛物线上是否存在点P,使得△PAC是以AC为底边的等腰三角形,若存在,请出点P的坐标及△PAC的面积,若不存在,请说明理由.