安徽省淮北市五校联考2022-2023学年九年级下学期第一次月考数学试题
试卷更新日期:2023-03-27 类型:月考试卷
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下图中几何体的左视图为( )
2. 下图中几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 若关于x的一元二次方程的一个根为 , 则m的值为( )A、0 B、1 C、或0 D、0或14. 如图,的三个顶点都在方格纸的格点上,则的值是( )
3. 若关于x的一元二次方程的一个根为 , 则m的值为( )A、0 B、1 C、或0 D、0或14. 如图,的三个顶点都在方格纸的格点上,则的值是( ) A、 B、 C、 D、5. 将分别写有“魅”“力”“安”“徽”四个汉字的小球装在一个不透明的口袋中,这些球除汉字不同外其他完全相同,每次摸球前先搅匀,随机摸出个球,放回后再随机摸出个球,两次摸出的球上的汉字可以组成“安徽”的概率是( )A、 B、 C、 D、6. 如图,点D是的中点,弦与交于点E, , 若 , 则的度数为( )
A、 B、 C、 D、5. 将分别写有“魅”“力”“安”“徽”四个汉字的小球装在一个不透明的口袋中,这些球除汉字不同外其他完全相同,每次摸球前先搅匀,随机摸出个球,放回后再随机摸出个球,两次摸出的球上的汉字可以组成“安徽”的概率是( )A、 B、 C、 D、6. 如图,点D是的中点,弦与交于点E, , 若 , 则的度数为( ) A、 B、 C、 D、7. 如图,在和中, , , 若 , , , 则的长为( ).
A、 B、 C、 D、7. 如图,在和中, , , 若 , , , 则的长为( ). A、2 B、 C、4 D、8. 如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若 , 则该圆锥底面半径为( )
A、2 B、 C、4 D、8. 如图,在矩形中,以点A为圆心,以长为半径画弧交于点E,将扇形剪下来做成圆锥,若 , 则该圆锥底面半径为( )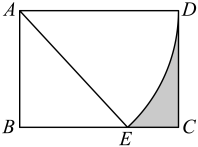 A、 B、 C、3 D、9. 在同一直角坐标系中,一次函数与二次函数的图像可能是( )A、
A、 B、 C、3 D、9. 在同一直角坐标系中,一次函数与二次函数的图像可能是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , , , 点D是斜边上的动点,将线段绕点B旋转至 , 连接 , , 则的最小值是( )
10. 如图,在中, , , , 点D是斜边上的动点,将线段绕点B旋转至 , 连接 , , 则的最小值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 , 则 .12. 已知一元二次方程的两个根为 , 则的值为 .13. 如图,反比例函数经过的直角边上一点C,且 , 若 , 则k= .
 14. 如图,在中, , , , 将绕点A逆时针旋转得到 , 点在上,连接 , .
14. 如图,在中, , , , 将绕点A逆时针旋转得到 , 点在上,连接 , . (1)、;(2)、 .
(1)、;(2)、 .三、解答题
-
15. 解方程: .16. 如图,在正方形网格中,的顶点都在小正方形的格点上.
 (1)、以点为位似中心,将放大2倍后得到 , 画出;(2)、找出的中点C,将绕点C旋转得到 , 画出 .17. 如图,一次函数的图像与x轴、y轴分别交于A,B两点,与反比例函数的图像分别交于C,D两点,已知点C的坐标是 , 且 , 求一次函数与反比例函数的解析式.
(1)、以点为位似中心,将放大2倍后得到 , 画出;(2)、找出的中点C,将绕点C旋转得到 , 画出 .17. 如图,一次函数的图像与x轴、y轴分别交于A,B两点,与反比例函数的图像分别交于C,D两点,已知点C的坐标是 , 且 , 求一次函数与反比例函数的解析式. 18. 观察下列各式:
18. 观察下列各式:第1个等式:;
第2个等式:;
第3个等式:;
请你根据上面三个等式提供的信息,解决下列问题.
(1)、请你写出第4个等式:;(2)、请你根据以上等式寻找规律,猜想第n个等式,并给出证明.19. 小瑞放学后回家,到小区的门口C处时,看到自己家的窗户A的仰角 , 他向前走了后到达点D处时,看到自己家窗户A的仰角 , 小瑞的身高 , 求小瑞家到地面的高度 . (结果取整数,参考数据: , , , , , , )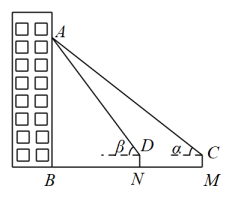 20. 如图,在中, , 以为直径作⊙O交于点D,过点D作于点E.
20. 如图,在中, , 以为直径作⊙O交于点D,过点D作于点E. (1)、求证:是⊙O的切线;(2)、若 , , 求的长.21. 某数学兴趣小组随机抽查了九年级部分同学在寒假期间每日用于学习的时间情况,记每日学习时间为(单位:小时),将调查的结果分成四个等级:A-学霸型;B-刻苦学习型;C-认真学习型;D-贪玩型 , 并将数据绘制成如图所示的条形统计图和扇形统计图.
(1)、求证:是⊙O的切线;(2)、若 , , 求的长.21. 某数学兴趣小组随机抽查了九年级部分同学在寒假期间每日用于学习的时间情况,记每日学习时间为(单位:小时),将调查的结果分成四个等级:A-学霸型;B-刻苦学习型;C-认真学习型;D-贪玩型 , 并将数据绘制成如图所示的条形统计图和扇形统计图. (1)、求抽查的总人数,并补全条形图;(2)、“学霸型”中的四位同学有两名来自九年级(2)班,另外两名来自其他班级,若从中任选两名同学来谈学习感悟,求选出的两名同学中,恰好有一名来自九年级(2)班的概率;(3)、若该校九年级学生有650人,则属于“贪玩型”的同学有多少人?22. 某商场试销一款玩具,进价为20元/件,商场与供货商约定,试销期间利润不高于 , 且同一周内售价不变.从试销记录看到,当售价为22元时,一周销售了80件该玩具;当售价为24元时,一周销售了60件该玩具.每周销量y(件)与售价x(元)符合一次函数关系.(1)、求每周销量y(件)与售价x(元)之间的关系式;(2)、若商场一周内销售该玩具获得的利润为210元,则该玩具的售价为多少元(3)、商场将该玩具的售价定为多少时,一周内销售该玩具获得利润最大最大利润W为多少元23. 已知矩形 , 将其绕着点A逆时针旋转得到矩形 .
(1)、求抽查的总人数,并补全条形图;(2)、“学霸型”中的四位同学有两名来自九年级(2)班,另外两名来自其他班级,若从中任选两名同学来谈学习感悟,求选出的两名同学中,恰好有一名来自九年级(2)班的概率;(3)、若该校九年级学生有650人,则属于“贪玩型”的同学有多少人?22. 某商场试销一款玩具,进价为20元/件,商场与供货商约定,试销期间利润不高于 , 且同一周内售价不变.从试销记录看到,当售价为22元时,一周销售了80件该玩具;当售价为24元时,一周销售了60件该玩具.每周销量y(件)与售价x(元)符合一次函数关系.(1)、求每周销量y(件)与售价x(元)之间的关系式;(2)、若商场一周内销售该玩具获得的利润为210元,则该玩具的售价为多少元(3)、商场将该玩具的售价定为多少时,一周内销售该玩具获得利润最大最大利润W为多少元23. 已知矩形 , 将其绕着点A逆时针旋转得到矩形 . (1)、如图1,若点E在上,连接 .
(1)、如图1,若点E在上,连接 .①求证:平分;
②连接交于点O,若 , , 求的长.
(2)、如图2,若点A,E,C在同一条直线上,与交于点M, , , 求的长.