山西省临汾市翼城县2023年中考一模数学试题

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 比1小4的数是（）

A、 $- 3$ B、3 C、 $- 5$ D、5

查看试题解析
2. 如图， $∠ A F E = 125 °$ ，如果 $A B ∥ C D$ ，那么 $∠ C$ 的度数为（）

A、 $75 °$ B、 $65 °$ C、 $55 °$ D、 $45 °$

查看试题解析
3. 在学校组织的以“赓续红色精神，歌咏崭新时代”为主题的钢琴演奏比赛中，全校共有18名学生进入决赛，他们的决赛成绩如下表所示．

成绩/分 9.40 9.50 9.60 9.70 9.80 9.90

人数 2 3 5 4 3 1

则这些学生决赛成绩的众数是（）

A、 $9.90$ B、 $9.80$ C、 $9.70$ D、 $9.60$

查看试题解析
4. 原子是化学变化中的最小微粒，按照国际单位制的规定，质量单位是“kg”．例如：1个氧原子的质量是 $2.657 \times 1 0^{- 26} k g$ ．如果小数0.000…02657用科学记数法表示为 $2.657 \times 1 0^{- 26}$ ，那么这个小数中的“0”有（）

A、25个 B、26个 C、27个 D、28个

查看试题解析
5. 下列四个几何体的俯视图中与众不同的是（）

A、 B、 C、 D、

查看试题解析
6. 将不等式组 ${\begin{array}{l} 1 - 4 x < 9 ， \\ 3 x - 5 \leq 1 \end{array}$ 的解集在数轴上表示出来，则下列选项正确的是（）

A、 B、 C、 D、

查看试题解析
7. 医用 $75 %$ 酒精消毒液可杀灭肠道致病杆菌、化脓性球菌、白色念珠菌，适用于人体的手部消毒和一般物体表面消毒．在一次实验中，要将 $2 k g$ 浓度为 $98 %$ 的酒精，稀释为 $75 %$ 的酒精，设需要加水 $x k g$ ．根据题意，下列方程正确的为（）

A、 $2 \times 0.98 = 0.75 x$ B、 $2 \times 0.75 = 0.98 x$ C、 $\frac{2 \times 0.98}{2 + x} = 0.75$ D、 $\frac{2 \times 0.75}{2 + x} = 0.98$

查看试题解析
8. 如图，在 $▱ A B C D$ 中，过点A作 $A E ⊥ B C$ ，垂足为E．若 $B C = 4$ ， $∠ C = 105 °$ ， $∠ B D C = 45 °$ ，则 $A E$ 的长为（）．

A、 $\frac{1 + \sqrt{3}}{2}$ B、 $1 + \sqrt{3}$ C、 $2 + \sqrt{3}$ D、 $2 + 2 \sqrt{3}$

查看试题解析
9. 如图，在平面直角坐标系内，四边形 $O A B C$ 是矩形，四边形 $A D E F$ 是正方形，点A，D在x轴的负半轴上，点F在 $A B$ 上，点B，E均在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上，若点B的坐标为 $(- 1 ， 6)$ ，则正方形 $A D E F$ 的周长为（）

A、4 B、6 C、8 D、10

查看试题解析
10. 如图， $△ A B C$ 内接于圆O，已知 $∠ A C B = 90 °$ ， $A C = B C$ ，顶点A，B，C恰好分别落在一组平行线中的三条直线上，若相邻两条平行线间的距离是1cm，则图中阴影部分的面积为（）

A、 $\frac{25 π - 50}{2} c m^{2}$ B、 $\frac{25 π - 25}{4} c m^{2}$ C、 $\frac{25 π - 50}{4} c m^{2}$ D、 $\frac{25 π - 25}{2} c m^{2}$

查看试题解析

二、填空题

11. 甲、乙两位同学各给出某函数的一个特征，甲：“函数值y随自变量x的增大而增大.”乙：“函数图象经过点 $(0 ， - 3)$ .”请你写出一个同时满足这两个特征的函数，其表达式是.

查看试题解析
12. 我国近十年的人口出生率及人口死亡率如图所示.
请根据该统计图，写出一条你获取的信息：.

查看试题解析
13. 根据 $2022$ 年8月 $16$ 日太原市市政府公布的《太原市推进城市空间立体绿化实施方案》，某小区积极进行小区绿化，计划种植A，B两种苗木共 $600$ 株.已知A种苗木的数量不小于B种苗木的数量的一半，若设A种苗木有x株，则可列不等式：.

查看试题解析
14. 如图，在平面直角坐标系中，已知点 $A (0 ， 3)$ ， $B (1 ， 0)$ ，将线段 $A B$ 先沿x轴正方向平移，然后沿y轴正方向平移，得到线段 $D C$ ，连接点B及其对应点C，若 $∠ A B C = 90 °$ ， $B C = 2 A B$ ，则点D的坐标是．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B = 45 °$ ， $∠ C = 60 °$ ， D为线段 $A B$ 的中点，点E，F分别在 $A C$ ， $B C$ 上， $B F = 3 F C$ ，且 $E F ∥ A B$ ，沿 $D E$ 将 $△ A D E$ 折叠得到 $△ G D E$ ，若 $A E = 2 \sqrt{3}$ ，则 $A G$ 的长是．

查看试题解析

三、解答题

16. 计算题。

(1)、计算： $\frac{3}{4} \times | - 2 | - {(- 2)}^{2} \times 2^{- 3}$ .

(2)、解二元一次方程组： ${\begin{array}{l} 2 y - x = - 4 ， \\ x + y = - 5 . \end{array}$

查看试题解析
17. 读诗词解题：大江东去浪淘尽，千古风流数人物，而立之年督东吴，早逝英年两位数，十位恰小个位三，个位平方与寿符，哪位学子算得快，多少年华属周瑜？（提示：三十而立，四十而不惑）

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A C$ 为直径的 $⊙ O$ 与 $A B$ 交于点D，过点B作 $B E ∥ A C$ ，与过点C的 $⊙ O$ 的切线相交于点E.求证： $B D = B E$ .

查看试题解析
19. 根据2022年8月山西省教育厅《高中阶段学校考试招生制度改革实施意见》的通知，自2022年秋季入学的七年级新生开始，山西省整体启动高中阶段学校考试招生制度改革工作，明确规定八年级地理、生物两个学科进行中考．期末考试后，七年级某班主任对自己班级学生的地理和生物总成绩（成绩取整数，每学科50分，满分为100分）作了统计分析、绘制成频数分布表和频数分布直方图（均不完整），请根据图表提供的信息，解答下列问题：
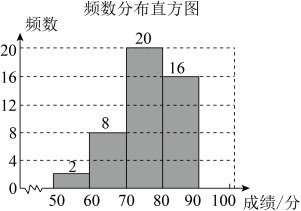
分组
频数
$50 < x \leq 60$
2
$60 < x \leq 70$
8
$70 < x \leq 80$
20
$80 < x \leq 90$
16
$90 < x \leq 100$
a
合计
50
频数分布表

(1)、求频数分布表中a的值，并补全频数分布直方图．

(2)、该校七年级共有900名学生．若成绩在80分以上的设为“优秀”，请估算该校七年级期末考试成绩为优秀的学生人数．

(3)、为了帮助该班学生有效学习地理和生物，该班主任随机从两科总成绩超过90分的学生中选2人分享学习经验.已知小红和小宇的成绩都超过90分，请用列表法或画树状图法求出小红和小宇都被选中的概率．

查看试题解析
20. 周末，小红和小宇相约一起去郊外劳动基地参加劳动.已知小红家B在小宇家A的北偏西 $25 °$ 方向上， $A B = 5 k m$ .两人到达劳动基地C处后，发现小宇家A在劳动基地C的南偏西 $25 °$ 方向上，小红家B在劳动基地C的南偏西 $70 °$ 方向上.求小宇家A到劳动基地C的距离 $A C$ .（结果保留1位小数；参考数据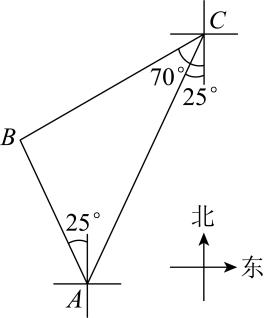： $s i n 50 ° \approx 0.77$ ， $c o s 50 ° \approx 0.64$ ， $t a n 50 ° \approx 1.19$ ， $\sqrt{2} \approx 1.41$ ）

查看试题解析

21. 阅读理解下面内容，并解决问题.

用求差法比较大小

学习了不等式的知识后，我们根据等式和不等式的基本性质，可知比较两个数或式子的大小可以通过求它们的差来判断．如果两个数或式子为m和n，那么

当 $m > n$ 时，一定有 $m - n > 0$ ；

当 $m = n$ 时，一定有 $m - n = 0$ ；

当 $m < n$ 时，一定有 $m - n < 0$ ．

反过来也符合题意，即

当 $m - n > 0$ 时，一定有 $m > n$ ；

当 $m - n = 0$ 时，一定有 $m = n$ ；

当 $m - n < 0$ 时，一定有 $m < n$ ．

因此，我们经常把要比较的对象先数量化，再求它们的差，根据差的正负判断对象的大小．这种比较大小的方法被称为“求差法”．

例如：已知 $a > b > c > 0$ ，比较 $\frac{a - c}{b}$ 与 $\frac{b - c}{a}$ 的大小．

解：

$\frac{a - c}{b} - \frac{b - c}{a} = \frac{a (a - c) - b (b - c)}{a b} = \frac{a^{2} - a c - b^{2} + b c}{a b} = \frac{(a^{2} - b^{2}) - (a - b) c}{a b} = \frac{(a - b) (a + b - c)}{a b}$

∵ $a > b > c > 0$ ，

∴ $a - b > 0$ ， $a b > 0$ ， $a + b - c > 0$ ，

∴ $\frac{(a - b) (a + b - c)}{a b} > 0$ ，

∴ $\frac{a - c}{b} > \frac{b - c}{a}$ ．

“求差法”的实质是把两个数（或式子）的大小判断的问题，转化为一个数（或式子）与0的大小比较的问题．一般步骤为①作差；②变形；③判断符号；④得出结论．

请解决以下问题：

(1)、用“

>

”或“

<

”填空：

3 - \sqrt{2}

4 - 2 \sqrt{2}

．

(2)、制作某产品有两种用料方案，方案1：用4块A型钢板，6块B型钢板；方案2：用3块A型钢板，7块B型钢板；已知A型钢板的面积比B型钢板的面积大，若A型钢板的面积为x，B型钢板的面积为y，则从省料的角度考虑，应选哪种方案？并说明理由．

(3)、已知

a > 0

，比较a与

\frac{1}{a}

的大小．

查看试题解析

22. 综合与实践

(1)、问题解决：
已知在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，四边形 $C D E F$ 是正方形，H为 $B F$ 所在的直线与 $A D$ 的交点；如图，当点F在 $A C$ 上时，请判断 $B F$ 和 $A D$ 的关系，并说明理由.

(2)、问题探究：
如图，将正方形 $C D E F$ 绕点C旋转，当点D在直线 $A C$ 右侧时，求证： $B H - A H = \sqrt{2} C H$ ；

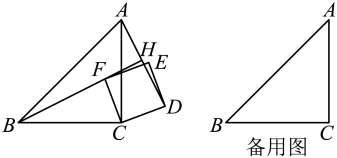(3)、问题拓展：
将正方形 $C D E F$ 绕点C旋转一周，当 $∠ A D C = 45 °$ 时，若 $A C = 3$ ， $C D = 1$ ，请直接写出线段 $A H$ 的长.

查看试题解析
23. 综合与探究
如图，在平面直角坐标系中，抛物线 $y = \frac{1}{4} x^{2} - \frac{3}{2} x - 4$ 与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C．将 $△ A B C$ 沿 $B C$ 所在的直线折叠，得到 $△ D B C$ ，点A的对应点为D．

(1)、求点A，B，C的坐标．

(2)、求直线 $B D$ 的函数表达式．

(3)、在抛物线上是否存在点P，使 $∠ P C B = ∠ A B C$ ？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

分组	频数
$50 < x \leq 60$	2
$60 < x \leq 70$	8
$70 < x \leq 80$	20
$80 < x \leq 90$	16
$90 < x \leq 100$	a
合计	50

成绩/分	9.40	9.50	9.60	9.70	9.80	9.90
人数	2	3	5	4	3	1