山东省青岛市市南区、市北区、崂山区2023年中考数学一模试卷
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 下列四个数中,属于有理数的是( )A、 B、 C、 D、2. 网络用语“6”是比较厉害的意思,且“6”本身是一个自然数,将数字用科学记数法表示( )A、 B、 C、 D、3. “中国结”是我国特有的手工编织工艺品,也是一种传统吉祥装饰物.下列四个中国结图案中,既是中心对称图形又是轴对称图形的有( )
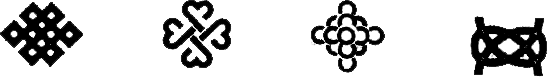 A、1个 B、2个 C、3个 D、4个4. 下列运算:①;②;③;④ , 其中结果正确的个数为( )A、1 B、2 C、3 D、45. 将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )
A、1个 B、2个 C、3个 D、4个4. 下列运算:①;②;③;④ , 其中结果正确的个数为( )A、1 B、2 C、3 D、45. 将一个正方体截一个角,得到如图所示的几何体,则这个几何体的俯视图是( )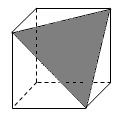 A、
A、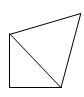 B、
B、 C、
C、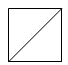 D、
D、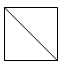 6. . 如图,在中, , 以点C为圆心,2为半径的圆与边相切于点D,与 , 分别交于点E和点F,点H是优弧上一点, , 则的度数是( )
6. . 如图,在中, , 以点C为圆心,2为半径的圆与边相切于点D,与 , 分别交于点E和点F,点H是优弧上一点, , 则的度数是( ) A、 B、 C、 D、7. 如图,在矩形ABCD中, , 点E为BC的中点,将沿AE折叠,使点B落在矩形内点F处,连接CF.则CF的长为( )
A、 B、 C、 D、7. 如图,在矩形ABCD中, , 点E为BC的中点,将沿AE折叠,使点B落在矩形内点F处,连接CF.则CF的长为( ) A、 B、 C、 D、8. 在同一直角坐标系中,一次函数y=ax﹣b和二次函数y=﹣ax2﹣b的大致图象是( )A、
A、 B、 C、 D、8. 在同一直角坐标系中,一次函数y=ax﹣b和二次函数y=﹣ax2﹣b的大致图象是( )A、 B、
B、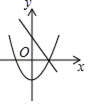 C、
C、 D、
D、
二、填空题
-
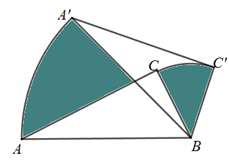
9. 计算:=.10. 关于x的函数的图象与x轴有两个交点,则k的取值范围是 .11. 元旦期间,某游乐场发布一游戏规则:在一个装有6个红球和若干个白球的不透明袋子中,随机摸出一个球,摸到红球就可获得欢动世界通票一张.已知有300人参加这个游戏,游乐场为此发放欢动世界通票60张,请你估计袋子中白球的数量是个.12. 某产品每件的生产成本为50元,原定销售价65元,经市场预测,从现在开始的第一季度销售价格将下降10%,第二季度又将回升5%.若要使半年以后的销售利润不变,设每个季度平均降低成本的百分率为x , 根据题意可列方程是 .13. 如图,在 中, , , . 绕点B顺时针方向旋转45°得到 ,点A经过的路径为弧 ,点C经过的路径为弧 ,则图中阴影部分的面积为.(结果保留 )
 14. 如图,在矩形 中,连接 ,过点C作 平分线 的垂线,垂足为点E , 且交 于点F;过点C作 平分线 的垂线,垂足为点H , 且交 于点G , 连接 ,若 , ,则线段 的长度为 .
14. 如图,在矩形 中,连接 ,过点C作 平分线 的垂线,垂足为点E , 且交 于点F;过点C作 平分线 的垂线,垂足为点H , 且交 于点G , 连接 ,若 , ,则线段 的长度为 .
三、解答题
-
15. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
如图, , D,E在上,作经过D,E两点且与相切.
 16. 计算:(1)、化简:;(2)、解不等式组: , 并写出它的最大整数解.17. 有四张反面完全相同的纸牌 , 其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.
16. 计算:(1)、化简:;(2)、解不等式组: , 并写出它的最大整数解.17. 有四张反面完全相同的纸牌 , 其正面分别画有四个不同的几何图形,将四张纸牌洗匀正面朝下随机放在桌面上.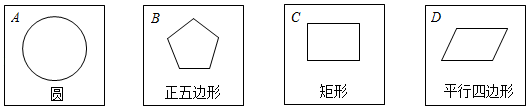 (1)、从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.18. 2022年北京冬奥会的召开惊艳世界,冬奥村的餐厅更是得到了各国运动员的好评.运动员主餐厅位于北京冬奥村居住区西南侧,共设置了世界餐台、亚洲餐台、中餐餐台、清真餐台、鲜果台、面包和甜品台等12种餐台.一送餐机器人从世界餐台A处向正南方向走200米到达亚洲餐台B处,再从B处向正东方向走500米到达中餐餐台C处,然后从C处向北偏西37°走到就餐区D处,最后从D回到A处,已知就餐区D在A的北偏东73°方向,求中餐台C到就餐区D(即CD)的距离.(结果保留整数)(参考数值: , , , , , . )
(1)、从四张纸牌中随机摸出一张,摸出的牌面图形是中心对称图形的概率是(2)、小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张,不放回.再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形既是轴对称图形又是中心对称图形,则小亮获胜,否则小明获胜.这个游戏公平吗?请用列表法(或画树状图)说明理由.(纸牌用表示)若不公平,请你帮忙修改一下游戏规则,使游戏公平.18. 2022年北京冬奥会的召开惊艳世界,冬奥村的餐厅更是得到了各国运动员的好评.运动员主餐厅位于北京冬奥村居住区西南侧,共设置了世界餐台、亚洲餐台、中餐餐台、清真餐台、鲜果台、面包和甜品台等12种餐台.一送餐机器人从世界餐台A处向正南方向走200米到达亚洲餐台B处,再从B处向正东方向走500米到达中餐餐台C处,然后从C处向北偏西37°走到就餐区D处,最后从D回到A处,已知就餐区D在A的北偏东73°方向,求中餐台C到就餐区D(即CD)的距离.(结果保留整数)(参考数值: , , , , , . ) 19. 2022年末,中国迎来第一波疫情高峰.为加强同学们的防护意识,某校举行了以“疫情防护”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图,下面为部分数据:其中“”这组的部分数据(从小到大排序)如下:80,82,82,83,83,84,85,85,85,86,87,87,87,88,88……其中“”这组的数据如下:90,92,93,95,95,96,96,96,97,100.
19. 2022年末,中国迎来第一波疫情高峰.为加强同学们的防护意识,某校举行了以“疫情防护”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图,下面为部分数据:其中“”这组的部分数据(从小到大排序)如下:80,82,82,83,83,84,85,85,85,86,87,87,87,88,88……其中“”这组的数据如下:90,92,93,95,95,96,96,96,97,100.竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
8
65
2
a
75
3
b
88
4
10
95

根据以上信息,回答下列问题:
(1)、下列说法正确的是____.A、样本为n名学生 B、a=12 C、m=40(2)、“”这组的数据的众数是 .(3)、随机抽取的这n名学生竞赛成绩的中位数是;平均分是;(4)、若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.20. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.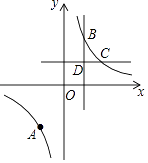 (1)、当y1﹣y2=4时,求m的值;
(1)、当y1﹣y2=4时,求m的值;
(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).
21. “冰墩墩”和“雪容融”作为第24届北京冬奥会和残奥会的吉祥物深受大家喜爱,某文旅店订购“冰墩墩”花费6000元,订购“雪容融”花费3200元,其中“冰墩墩”的订购单价比“雪容融”的订购单价多20元,并且订购“冰墩墩”的数量是“雪容融”的1.25倍.(1)、求文旅店订购“冰墩墩”和“雪容融”的数量分别是多少个;(请列分式方程作答)(2)、该文旅店以100元和80元的单价销售“冰墩墩”和“雪容融”,在“冰墩墩”售出 , “雪容融”售出后,文旅店为了尽快回笼资金,决定对剩余的“冰墩墩”每个打a折销售,对剩余的“雪容融”每个降价2a元销售,很快全部售完,若要保证文旅店总利润不低于6060元,求a的最小值.22. 已知:如图,正方形的对角线相交于点O,的平分线分别交 , 于点E,F,作于点H,分别交 , 于点G,P,连接 , .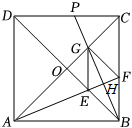 (1)、求证:;(2)、判断四边形是什么特殊四边形?并证明你的结论.23. 某企业生产一种新产品,每件成本50元.(1)、由于新产品市场占有率较低,去年上市初期销量逐渐减少,1至6月,图销售量(件)与月份x(月)满足一次函数关系;随着新产品逐渐得到市场认可,销量增加,6至12月,月销售量(件)与月份x(月)满足二次函数关系,且6月份的月销售量是该二次函数的最小值,函数关系如图所示.
(1)、求证:;(2)、判断四边形是什么特殊四边形?并证明你的结论.23. 某企业生产一种新产品,每件成本50元.(1)、由于新产品市场占有率较低,去年上市初期销量逐渐减少,1至6月,图销售量(件)与月份x(月)满足一次函数关系;随着新产品逐渐得到市场认可,销量增加,6至12月,月销售量(件)与月份x(月)满足二次函数关系,且6月份的月销售量是该二次函数的最小值,函数关系如图所示.
①分别求出、与x之间的函数关系式;
②已知去年1至6月每件该产品的售价z(元)与月份x之间满足函数关系:( , x为整数),除成本外,平均每销售一件产品还需额外支出杂费p元,p与月份x之间满足函数关系:( , x为整数)从7月至12月每件产品的售价和杂费均稳定在6月的水平.去年1至12月,该产品在第几月获得最大利润?并求出最大利润.
(2)、今年以来,由于物价上涨及积压了去年未销售的产品等因素,该企业每月均需支出杂费6000元(不论每月销售量如何,且天数不满一月时,按整月计算).为了出售去年积压的4000件该产品,企业计划以单价70元销售,每月可卖出350件.为了尽快回笼资金并确保获利,企业决定降价销售,每降价1元(降价金额为整数),每月可多卖出50件,且要求在5个月内(含5个月)将这批库存全部售出,如何定价可使获利最大?24. 某数学兴趣小组在数学课外活动中,对矩形内两条互相垂直的线段做了如下探究: (1)、 [观察与猜想]
(1)、 [观察与猜想]如图①,在正方形中,点E、F分别是、上的两点,连接、 , , 则的值为=;
(2)、如图②,在矩形中, , , 点E是上的一点,连接 , , 且 , 则的值为 .(3)、 [性质探究]如图③,在四边形中, . 点E为上一点,连接 , 过点C作的垂线交的延长线于点G,交的延长线于点F.求证:;
(4)、[拓展延伸]已知四边形是矩形, ,如图④,点P是上的点,过点P作 , 垂足为O,点O恰好落在对角线上.求的值;
(5)、如图⑤,点P是上的一点,过点P作 , 垂足为O,点O恰好落在对角线上,延长、交于点G.当时, .25. 已知:如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD垂直平分AC.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动,另一个点也停止运动.过点P作PE⊥AB,交BC于点E,过点Q作QF∥AC,分别交AD,OD于点F,G.连接OP,EG.设运动时间为t(s)(0<t<5),解答下列问题: (1)、当t为何值时,点E在∠BAC的平分线上?(2)、设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)、连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,点E在∠BAC的平分线上?(2)、设四边形PEGO的面积为S(cm2),求S与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大?若存在,求出t的值;若不存在,请说明理由;(4)、连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ?若存在,求出t的值;若不存在,请说明理由.