山东省菏泽市东明县2023年中考一模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 拒绝“餐桌浪费”,刻不容缓.节约一粒米的账:一个人一日三餐少浪费一粒米,全国一年就可以节省32400000斤,“32400000”这个数据用科学记数法表示为( )A、 B、 C、 D、3. 如图所示是一个正方体的展开图,图中的六个正方形内分别标有:有、志、者、事、竟、成,将其围成一个正方体后,与“有”所在面相对面上的字是( )
 A、竟 B、成 C、事 D、者4. 一个螺母如图放置,则它的左视图是( )
A、竟 B、成 C、事 D、者4. 一个螺母如图放置,则它的左视图是( )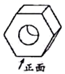 A、
A、 B、
B、 C、
C、 D、
D、 5. 疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
5. 疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )金额/元
10
20
30
50
100
人数
2
18
10
8
2
A、平均数为元 B、众数为元 C、中位数为元 D、极差为元6. 某口袋里现有12个红球和若干个绿球(两种球除颜色外,其余完全相同),某同学随机的从该口袋里摸出一球,记下颜色后放回,共试验600次,其中有300次是红球,估计绿球个数为( )A、8 B、10 C、12 D、147. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC 与△ADE 相似 的是( )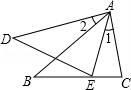 A、∠C=∠AED B、∠B=∠D C、 = D、 =8. 将一个长方形纸片按如图所示的方式折叠,、为折痕,若 , 则等于( )
A、∠C=∠AED B、∠B=∠D C、 = D、 =8. 将一个长方形纸片按如图所示的方式折叠,、为折痕,若 , 则等于( )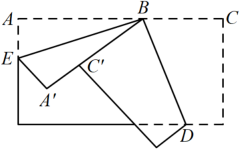 A、 B、 C、 D、9. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、 B、 C、 D、9. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )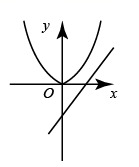 A、
A、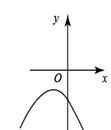 B、
B、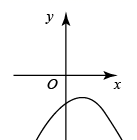 C、
C、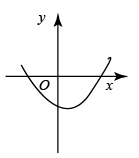 D、
D、 10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
10. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )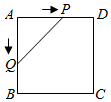 A、
A、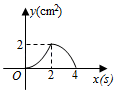 B、
B、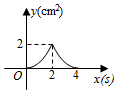 C、
C、 D、
D、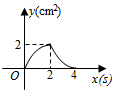
二、填空题
-
11. 分解因式: .12. 已知 , 则的值为 .13. 已知一个n边形的内角和等于1980°,则n= .14. 如图,两个圆的圆心重合,大圆的半径是R,小圆的面积是大圆面积的 , 则阴影部分的面积是.(结果保留π)
 15. 如图, , 于A,于 , 且 , 点P从B向A运动,每秒钟走 , Q点从B向D运动,每秒钟走 , 点P,Q同时出发,运动秒后,与全等.
15. 如图, , 于A,于 , 且 , 点P从B向A运动,每秒钟走 , Q点从B向D运动,每秒钟走 , 点P,Q同时出发,运动秒后,与全等. 16. 如图,用棋子摆成的“T”形图,按这样的规律摆下去,第2023个需要枚棋子.
16. 如图,用棋子摆成的“T”形图,按这样的规律摆下去,第2023个需要枚棋子.
三、解答题
-
17.(1)、计算: .(2)、解不等式组:18. 先化简,再求值: , 其中 , .19. 课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.很好;B.较好;C.一般;D.较差.并将调查结果绘制成以下两幅不完整的统计图,请你据统计图解答下列问题:
 (1)、王老师一共调查了多少名同学;(2)、C类女生有名,D类男生有名,并将上面的条形统计图补充完整;(3)、为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习.请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.20. 如图,一次函数y=ax+1(a≠0)的图象与x轴交于点A,与反比例函数y=的图象在第一象限交于点B(1,3),过点B作BC⊥x轴于点C.
(1)、王老师一共调查了多少名同学;(2)、C类女生有名,D类男生有名,并将上面的条形统计图补充完整;(3)、为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习.请用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.20. 如图,一次函数y=ax+1(a≠0)的图象与x轴交于点A,与反比例函数y=的图象在第一象限交于点B(1,3),过点B作BC⊥x轴于点C. (1)、求一次函数和反比例函数的解析式.(2)、求△ABC的面积.21. 毕业在即,某商店抓住商机,准备购进一批纪念品,若商店花440元可以购进50本学生纪念品和10本教师纪念品,其中教师纪念品的成本比学生纪念品的成本多8元.(1)、请问这两种不同纪念品的成本分别是多少?(2)、如果商店购进1200个学生纪念品,第一周以每个10元的价格售出400个,第二周若按每个10元的价格仍可售出400个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余学生纪念品清仓处理,以每个4元的价格全部售出,如果这批纪念品共获利2500元,问第二周每个纪念品的销售价格为多少元?22. 如图,在中, , O是边上一点,以O为圆心,为半径的圆与相交于点D,连接 , 且 .
(1)、求一次函数和反比例函数的解析式.(2)、求△ABC的面积.21. 毕业在即,某商店抓住商机,准备购进一批纪念品,若商店花440元可以购进50本学生纪念品和10本教师纪念品,其中教师纪念品的成本比学生纪念品的成本多8元.(1)、请问这两种不同纪念品的成本分别是多少?(2)、如果商店购进1200个学生纪念品,第一周以每个10元的价格售出400个,第二周若按每个10元的价格仍可售出400个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价),单价降低x元销售一周后,商店对剩余学生纪念品清仓处理,以每个4元的价格全部售出,如果这批纪念品共获利2500元,问第二周每个纪念品的销售价格为多少元?22. 如图,在中, , O是边上一点,以O为圆心,为半径的圆与相交于点D,连接 , 且 . (1)、求证:是的切线;(2)、若 , 求半径的长.
(1)、求证:是的切线;(2)、若 , 求半径的长.

