河北省邢台市2023年中考数学一模试卷

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. $4 s i n^{2} 60 °$ 的值为（）

A、3 B、1 C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 已知反比例函数 $y = - \frac{4}{x}$ ，当 $x \leq - 2$ 时，y有（）

A、最小值 $2$ B、最大值 $2$ C、最小值 $- 2$ D、最大值 $- 2$

查看试题解析
3. 某个几何体的三视图如图所示，该几何体是（）

A、 B、 C、 D、

查看试题解析
4. 嘉淇准备解一元二次方程 $4 x^{2} + 7 x + ■ = 0$ 时，发现常数项被污染，若该方程有实数根，则被污染的数可能是（）

A、3 B、5 C、6 D、8

查看试题解析
5. 如图，在由小正方形组成的网格中，点A，B，C，D，E，F，O均在格点上．下列三角形中，外心不是点O的是（）

A、 $△ A B C$ B、 $△ A B D$ C、 $△ A B E$ D、 $△ A B F$

查看试题解析
6. 如图，在平面直角坐标系中， $△ A B C$ 与 $△ D E F$ 关于原点 $O$ 位似，且 $O B = 2 O E$ ，若 $S_{△ A B C} = 4$ ，则 $S_{△ D E F}$ 为（）

A、 $1$ B、 $2$ C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
7. 关于抛物线 $C_{1}$ ： $y_{1} = 2 x^{2} - 1$ 与 $C_{2}$ ： $y_{2} = 2 {(x - 2)}^{2} - 3$ ，下列说法错误的是（）

A、两条抛物线的形状相同 B、抛物线 $C_{1}$ 通过平移可以与 $C_{2}$ 重合 C、抛物线 $C_{1}$ 与 $C_{2}$ 的对称轴相同 D、两条抛物线均与x轴有两个交点

查看试题解析
8. 下列说法正确的是（）

A、“将三条线段首尾顺次相接可以组成三角形”是必然事件 B、如果明天降水的概率是 $50 %$ ，那么明天有半天都在降雨 C、数据 $4$ ， $5$ ， $5$ ， $4$ ， $3$ 中没有众数 D、若A，B两组数据的平均数相同， $s_{A}^{2} = 0.01$ ， $s_{B}^{2} = 1$ ，则A组数据较稳定

查看试题解析
9. 如图，电线杆AB的中点C处有一标志物，在地面D点处测得标志物的仰角为32°，若点D到电线杆底部点B的距离为a米，则电线杆AB的长可表示为（）

A、2a·cos32°米 B、2a·tan32°米 C、 $\frac{2 a}{s i n 32 °}$ 米 D、 $\frac{2 a}{t a n 32 °}$ 米

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ A D C = ∠ B A C$ ，则添加下列条件后，不能判定 $△ A D C$ 和 $△ B A C$ 相似的是（）

A、 $C A$ 平分 $∠ B C D$ B、 $∠ D A C = ∠ A B C$ C、 $\frac{A C}{B C} = \frac{C D}{A C}$ D、 $\frac{A D}{A B} = \frac{C D}{A C}$

查看试题解析
11. 一个球从地面竖直向上弹起时的速度为8米/秒，经过t秒时球的高度为h米，h和t满足公式：h=v₀t- $\frac{1}{2}$ gt²(v₀表示球弹起时的速度，g表示重力系数，取g=10米/秒²)，则球不低于3米的持续时间是（）

A、 $0.4$ 秒 B、 $0.6$ 秒 C、 $0.8$ 秒 D、1秒

查看试题解析
12. 如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A，B，并使 $A B$ 与车轮内圆相切于点D，半径 $O C ⊥ A B$ 交外圆于点C，测得 $C D = 10 c m$ ， $A B = 60 c m$ ，则这个车轮的外圆半径是（　　）

A、10cm B、30cm C、60cm D、50cm

查看试题解析
13. 德尔塔（Delta）是一种全球流行的新冠病毒变异毒株，其传染性极强．某地有1人感染了德尔塔，因为没有及时隔离治疗，经过两轮传染后，一共有144人感染了德尔塔病毒，下面所列方程正确的是（）

A、 $1 + x + x^{2} = 144$ B、 $x (x + 1) = 144$ C、 $1 + x + x (x + 1) = 144$ D、 $1 + (1 + x) + x (x + 1) = 144$

查看试题解析
14. 如图，已知AB是半圆O的直径，点C，D将 $A B$ 分成相等的三段弧，点M在 $A B$ 的延长线上，连接 $M D$ ．对于下列两个结论，判断正确的是（）
结论I：若 $∠ O M D = 30 °$ ，则 $M D$ 为半圆O的切线；
结论II：连接 $A C ， C D$ ，则 $∠ A C D = 130 °$

A、I和II都对 B、I对II错 C、I错II对 D、I和II都错

查看试题解析
15. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是直线 $x = - 2$ ，并与x轴交于A，B两点，且 $O A = 5 O B$ ，下列结论错误的是（）

A、 $a b c > 0$ B、 $b - 4 a = 0$ C、 $a + b + c > 0$ D、若m为任意实数，则 $a m^{2} + b m \leq 4 a - 2 b$

查看试题解析
16. 题目：“如图，在矩形 $A B C D$ 中， $A B = 9$ ， $B C = 15$ ， P，Q分别是 $B C ， C D$ 上的点．”张老师要求添加条件后，编制一道题目，并解决，甲、乙两人的做法如下．下列判断正确的是（）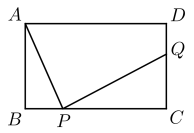
甲：若 $C Q = 4$ ，则在BC上存在2个点P，使 $△ A B P$ 与 $△ P C Q$ 相似；
乙：若 $A P ⊥ P Q$ ，则 $C Q$ 的最大值为 $\frac{25}{4}$

A、甲对乙错 B、甲错乙对 C、甲、乙都对 D、甲、乙都错

查看试题解析

二、填空题

17. 在一个不透明的口袋中装有12个白球，16个黄球，24个红球，28个绿球，除颜色不同外其余都相同，小明通过多次摸球试验后发现，摸到某种颜色的球的频率稳定在0.3左右，则小明做试验时所摸到的球的颜色是．

查看试题解析
18. 如图，从一个边长为 $2$ 的铁皮正六边形 $A B C D E F$ 上，剪出一个扇形 $C A E$ ．

(1)、 $∠ A C E$ 的度数为．

(2)、若将剪下来的扇形 $C A E$ 围成一个圆锥，则该圆锥的底面半径为．

查看试题解析
19. 如图，在平面直角坐标系中，已知双曲线 $y = \frac{k}{x} (k < 0 ， x < 0)$ 把 $R t △ A O B$ 分成 $W_{1}$ ， $W_{2}$ 两部分，且与 $A B ， O A$ 交于点C，D，点A的坐标为 $(- 6 ， 4)$ ．

(1)、连接 $O C$ ，若 $S_{△ O A C} = 9$ ．
①k的值为；
②点D的坐标为；

(2)、若 $W_{1}$ 内（不含边界）的整点（横、纵坐标均为整数的点）与 $W_{2}$ 内（不含边界）的整点个数比为 $3 ： 4$ ，则k的取值范围是．

查看试题解析

三、解答题

20. 嘉嘉解方程 $x^{2} + 2 x - 3 = 0$ 的过程如表所示．
解方程： $x^{2} + 2 x - 3 = 0$
解： $x^{2} + 2 x = 3 \dots \dots$ 第一步
${(x + 1)}^{2} = 3 \dots \dots$ 第二步
$x_{1} = \sqrt{3} - 1$ ， $x_{2} = - \sqrt{3} - 1 \dots \dots$ 第三步

(1)、嘉嘉是用（填“配方法”“公式法”或“因式分解法”）来求解的；从第步开始出现错误；

(2)、请你用不同于（1）中的方法解该方程．

查看试题解析
21. 如图，小欢从公共汽车站 $A$ 出发，沿北偏东 $30 °$ 方向走 $2000$ 米到达东湖公园B处，参观后又从B处沿正南方向行走一段距离，到达位于公共汽车站南偏东 $45 °$ 方向的图书馆C处．

(1)、求小欢从东湖公园走到图书馆的途中与公共汽车站之间的最短距离；

(2)、如果小欢以 $100$ 米 $/$ 分的速度从图书馆C沿 $C A$ 回到公共汽车站A，那么她在 $15$ 分钟内能否到达公共汽车站？ $($ 注： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732)$

查看试题解析
22. 如图1，将一长方体A放置于一水平玻璃桌面上，按不同的方式摆放，记录桌面所受压强 $P (P a)$ 与受力面积 $S (m^{2})$ 的关系如下表所示(与长方体A相同重量的长方体均满足此关系)．
桌面所受压强 $P (P a)$
$100$
$200$
$400$
$500$
$800$
受力面积 $S (m^{2})$
$2$
$1$
$0.5$
$0.4$
$a$

(1)、根据数据，求桌面所受压强 $P (P a)$ 与受力面积 $S (m^{2})$ 之间的函数表达式及a的值；

(2)、现想将另一长、宽、高分别为 $0.2 m$ ， $0.1 m$ ， $0.3 m$ ，且与长方体A相同重量的长方体按如图 $2$ 所示的方式放置于该水平玻璃桌面上．若该玻璃桌面能承受的最大压强为 $5000 P a$ ，请你判断这种摆放方式是否安全？并说明理由，

查看试题解析
23. 为奖励期末考试优异的学生，王老师去文具店购买笔记本，购买情况如图所示．

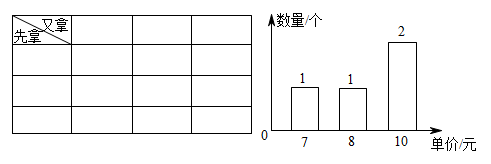(1)、王老师购买笔记本的平均价格为元；若从中随机拿出一个笔记本，则拿到10元笔记本的概率为；

(2)、若王老师已拿出一个10元笔记本后，准备从剩余3个笔记本中随机再拿出一个本．
①所剩的3个笔记本价格的中位数与原来4个笔记本价格的中位数是否相同？并说明理由；
②在剩余的3个笔记本中，若王老师先随机拿出一个笔记本后放回，之后又随机拿一个笔记本，用列表法（如上表）求王老师两次都拿到相同价格的笔记本的概率．

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $D ， E$ 分别为边 $A B ， A C$ 上的点，且 $D E ∥ B C$ ．已知 $B C = 10$ ， $\frac{A D}{D B} = \frac{3}{2}$ ．

(1)、 $D E$ 的长为； $△ A D E$ 与 $△ A B C$ 的周长比为；

(2)、将 $△ A D E$ 绕点A旋转，连接 $B D ， C E$ ．
①当 $△ A D E$ 旋转至图2所示的位置时，求证： $△ A B D ∽ △ A C E$ ；
②如图3，当 $△ A D E$ 旋转至点D在 $B C$ 上时， $A D ⊥ B C$ ，直接写出 $A B$ 及 $E C$ 的长．

查看试题解析
25. 如图，已知点A（0，2），B（2，2），C（－1，－2），抛物线F： $y = x^{2} - 2 m x + m^{2} - 2$ 与直线x=－2交于点P.

(1)、当抛物线F经过点C时，求它的表达式；

(2)、设点P的纵坐标为 $y_{P}$ ，求 $y_{P}$ 的最小值，此时抛物线F上有两点 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，且 $x_{1} < x_{2}$ ≤－2，比较 $y_{1}$ 与 $y_{2}$ 的大小；

(3)、当抛物线F与线段AB有公共点时，直接写出m的取值范围.

查看试题解析
26. 在等边三角形 $A B C$ 中， $A D ⊥ B C$ 于点D，半圆O的直径 $E F$ 开始在边 $B C$ 上，且点E与点C重合， $E F = 4$ ．将半圆O绕点C顺时针旋转 $α (0 ° < α \leq 90 °)$ ，当 $α = 60 °$ 时，半圆O与 $A D$ 相切于点P．如图1所示．

(1)、求 $A C$ 的长度；

(2)、如图2．当 $A C$ ， $B C$ 分别与半圆O交于点M，N时，连接 $M N$ ， $O M$ ， $O N$ ．
①求 $∠ M O N$ 的度数；
②求 $M N$ 的长度；

(3)、当 $α = 90 °$ 时，将半圆O沿边 $B C$ 向左平移，设平移距离为x．当 $\overset{⌢}{E F}$ 与 $△ A B C$ 的边一共有两个交点时，直接写出x的取值范围．

查看试题解析

桌面所受压强 $P (P a)$	$100$	$200$	$400$	$500$	$800$
受力面积 $S (m^{2})$	$2$	$1$	$0.5$	$0.4$	$a$