河北省唐山市滦州市2023年九年级摸底考试数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 若使得算式-2□0.25的值最小,则“□”中填入的运算符号是( )A、+ B、- C、× D、÷2. 国家统计局发布数据显示,年出生人口人.数据“”用科学记数法表示为( )A、 B、 C、 D、3. 如图,用5个小正方体分别摆成甲、乙两个几何体,对于其三视图说法正确的是( )
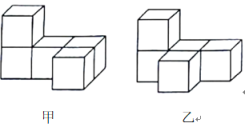 A、主视图、俯视图,左视图都相同 B、主视图、俯视图都相同 C、俯视图,左视图都相同 D、主视图、左视图都相同4. 下列各式正确的是( )A、=±4 B、=3 C、=-8 D、4-4=5. 下列计算正确的是( )A、 B、 C、 D、6. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、87. 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则∠O的度数为( )
A、主视图、俯视图,左视图都相同 B、主视图、俯视图都相同 C、俯视图,左视图都相同 D、主视图、左视图都相同4. 下列各式正确的是( )A、=±4 B、=3 C、=-8 D、4-4=5. 下列计算正确的是( )A、 B、 C、 D、6. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、87. 如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则∠O的度数为( ) A、30° B、45° C、60° D、75°8. 如图,在△ABC中,∠ABC=90°,EF、BG分别是△ABC的中位线和中线,则下列说法错误的是( )
A、30° B、45° C、60° D、75°8. 如图,在△ABC中,∠ABC=90°,EF、BG分别是△ABC的中位线和中线,则下列说法错误的是( ) A、 B、 C、 D、9. 一组数据3,5,5,7,若添加一个数据5,则发生变化的统计量是( )A、平均数 B、中位数 C、方差 D、众数10. 如图,直线 , 将三角板按如图方式放置,直角顶点在上.若 , 则( )
A、 B、 C、 D、9. 一组数据3,5,5,7,若添加一个数据5,则发生变化的统计量是( )A、平均数 B、中位数 C、方差 D、众数10. 如图,直线 , 将三角板按如图方式放置,直角顶点在上.若 , 则( ) A、36° B、45° C、54° D、64°11. 把一张长方形纸片按如图①,图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
A、36° B、45° C、54° D、64°11. 把一张长方形纸片按如图①,图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )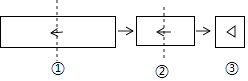 A、
A、 B、
B、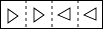 C、
C、 D、
D、 12. 如图,在▱ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则▱ABCD的周长为( )
12. 如图,在▱ABCD中,对角线AC的垂直平分线分别交AD,BC于点E,F,连接CE,若△CED的周长为6,则▱ABCD的周长为( ) A、6 B、12 C、18 D、2413. 某超市销售一种饮料,每瓶进价为6元.当每瓶售价为10元时,日均销售量为160瓶,经市场调查表明,每瓶售价每增加1元,日均销售量减少20瓶.若超市计划该饮料日均总利润为700元,且尽快减少库存,则每瓶该饮料售价为( )A、11 B、12 C、13 D、1414. 如图,在 中, , ,则 的度数是( )
A、6 B、12 C、18 D、2413. 某超市销售一种饮料,每瓶进价为6元.当每瓶售价为10元时,日均销售量为160瓶,经市场调查表明,每瓶售价每增加1元,日均销售量减少20瓶.若超市计划该饮料日均总利润为700元,且尽快减少库存,则每瓶该饮料售价为( )A、11 B、12 C、13 D、1414. 如图,在 中, , ,则 的度数是( ) A、 B、 C、 D、15. 疫情期间进行线上教学,为保证学生的身体健康,某校规定四项特色活动:舞蹈、跳绳、踢毽、武术,要求每位学生任选一项在家锻炼,小明从全校1200名学生中随机调查了部分学生,对他们所选活动进行了统计,并绘制了尚不完整的条形图和扇形图,如图所示,下列结论错误的是( )
A、 B、 C、 D、15. 疫情期间进行线上教学,为保证学生的身体健康,某校规定四项特色活动:舞蹈、跳绳、踢毽、武术,要求每位学生任选一项在家锻炼,小明从全校1200名学生中随机调查了部分学生,对他们所选活动进行了统计,并绘制了尚不完整的条形图和扇形图,如图所示,下列结论错误的是( )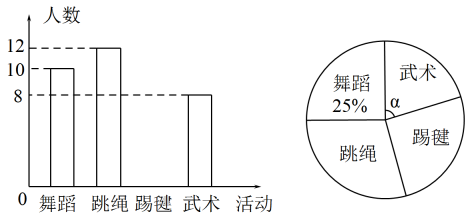 A、调查了40名学生 B、被调查的学生中,选踢毽的有10人 C、 D、全校选舞蹈的估计有250人16. 如图,在矩形纸片中, , , 沿对角线剪开(如图1);固定 , 把沿方向平移(如图2),当两个三角形重叠部分的面积最大时,移动的距离等于( ).
A、调查了40名学生 B、被调查的学生中,选踢毽的有10人 C、 D、全校选舞蹈的估计有250人16. 如图,在矩形纸片中, , , 沿对角线剪开(如图1);固定 , 把沿方向平移(如图2),当两个三角形重叠部分的面积最大时,移动的距离等于( ). A、1 B、1.5 C、2 D、3
A、1 B、1.5 C、2 D、3二、填空题
-
17. 已知 , 则 .18. 如图,已知海岛B在海岛A的正东方向,从海岛A观测货船C在其北偏东方向上,从海岛B观察货船C在其北偏东方向上,则的度数是 .
 19. 如图是某种电子理疗设备工作原理的示意图,其开始工作时的温度是 , 然后按照一次函数关系一直增加到 , 这样有利于打通病灶部位的血液循环,在此温度下再沿反比例函数关系缓慢下降至 , 然后在此基础上又沿着一次函数关系一直将温度升至 , 再在此温度下沿着反比例函数关系缓慢下降至,如此循环下去.
19. 如图是某种电子理疗设备工作原理的示意图,其开始工作时的温度是 , 然后按照一次函数关系一直增加到 , 这样有利于打通病灶部位的血液循环,在此温度下再沿反比例函数关系缓慢下降至 , 然后在此基础上又沿着一次函数关系一直将温度升至 , 再在此温度下沿着反比例函数关系缓慢下降至,如此循环下去. (1)、t的值为;(2)、如果在分钟内温度大于或等于时,治疗效果最好,则维持这个温度范围的持续时间为分钟.
(1)、t的值为;(2)、如果在分钟内温度大于或等于时,治疗效果最好,则维持这个温度范围的持续时间为分钟.三、解答题
-
20. 琪琪在电脑中设置了一个有理数的运算程序:输入数“a”加“★”键再输入“b”,就可以得到运算 .(1)、按此程序;(2)、若琪琪输入数“-1”加“★”键再输入“x”后,电脑输出的数为1,求x的值;(3)、嘉嘉运用琪琪设置的在这个程序时,屏幕显示:“该操作无法进行,”你能说出嘉嘉在什么地方出现问题了吗?21. 观察下列式子:① , ② , ③ ,(1)、请写出第5个等式:;(2)、根据你发现的规律,请写出第n个等式: .(3)、试用所学知识说明你所写出的等式的正确性;22. 如图,的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
 (1)、若乙固定在E处,移动甲后黑色方块构成的拼图是中心对称图形的概率是;(2)、若甲、乙均可在本层移动,用画树状图法或列表法求出黑色方块所构成拼图是轴对称图形的概率.23. 某零售店销售甲、乙两种蔬菜,甲种蔬菜每千克获利1.1元,乙种蔬菜每千克获利1.5元.该店计划一次购进这两种蔬菜共56千克,并能全部售出.设该店购进甲种蔬菜x千克,销售这56千克蔬菜获得的总利润为y元.(1)、求y与x的关系式;(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 , 则该店购进甲、乙两种蔬菜各多少千克时,获得的总利润最大?24. 如图,在中, , 以为直径作 , 分别交边和边于点和点 , 过点作交于点 , 延长交的延长线于点 , 过点作于点 .
(1)、若乙固定在E处,移动甲后黑色方块构成的拼图是中心对称图形的概率是;(2)、若甲、乙均可在本层移动,用画树状图法或列表法求出黑色方块所构成拼图是轴对称图形的概率.23. 某零售店销售甲、乙两种蔬菜,甲种蔬菜每千克获利1.1元,乙种蔬菜每千克获利1.5元.该店计划一次购进这两种蔬菜共56千克,并能全部售出.设该店购进甲种蔬菜x千克,销售这56千克蔬菜获得的总利润为y元.(1)、求y与x的关系式;(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 , 则该店购进甲、乙两种蔬菜各多少千克时,获得的总利润最大?24. 如图,在中, , 以为直径作 , 分别交边和边于点和点 , 过点作交于点 , 延长交的延长线于点 , 过点作于点 . (1)、试判断与的位置关系,并说明理由;(2)、证明:;(3)、若 , , 求图中阴影部分的面积.25. 如图,x轴上依次有A,B,D,C四个点,且 , 从点A处向右上方沿抛物线发出一个带光的点P.
(1)、试判断与的位置关系,并说明理由;(2)、证明:;(3)、若 , , 求图中阴影部分的面积.25. 如图,x轴上依次有A,B,D,C四个点,且 , 从点A处向右上方沿抛物线发出一个带光的点P. (1)、求点A的横坐标,且在图中补画出y轴;(2)、通过计算说明点P是否会落在点C处;(3)、求抛物线的顶点坐标和对称轴;(4)、在x轴上从左到右有两点E,F,且 , 从点F向上作轴,且 . 在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边EG(包括端点)上,直接写出点G横坐标的最大值与最小值.26. 如图,在中,AB=AC,E是线段BC上一动点(不与B、C重合),连接AE,将线段AE绕点A逆时针旋转与相等的角度,得到线段AF,连接 . 点和点分别是边 , 的中点.
(1)、求点A的横坐标,且在图中补画出y轴;(2)、通过计算说明点P是否会落在点C处;(3)、求抛物线的顶点坐标和对称轴;(4)、在x轴上从左到右有两点E,F,且 , 从点F向上作轴,且 . 在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边EG(包括端点)上,直接写出点G横坐标的最大值与最小值.26. 如图,在中,AB=AC,E是线段BC上一动点(不与B、C重合),连接AE,将线段AE绕点A逆时针旋转与相等的角度,得到线段AF,连接 . 点和点分别是边 , 的中点. (1)、【问题发现】如图1,若 , 当点E是边的中点时, , 直线与相交所成的锐角的度数为度.(2)、【解决问题】如图2,若 , 当点E是边上任意一点时(不与B、C重合),上述两个结论是否成立?若成立,请写出证明过程;若不成立,请说明理由.(3)、【拓展探究】如图3,若 , AB=6, , 在E点运动的过程中,直接写出GN的最小值.
(1)、【问题发现】如图1,若 , 当点E是边的中点时, , 直线与相交所成的锐角的度数为度.(2)、【解决问题】如图2,若 , 当点E是边上任意一点时(不与B、C重合),上述两个结论是否成立?若成立,请写出证明过程;若不成立,请说明理由.(3)、【拓展探究】如图3,若 , AB=6, , 在E点运动的过程中,直接写出GN的最小值.