河北省秦皇岛市开发区2023年中考数学模拟试卷

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 从原点开始向左移动3个单位，再向右移动1个单位后到达A点，则A点表示的数是（）

A、3 B、4 C、2 D、－2

查看试题解析
2. 下列图形中，是中心对称但不是轴对称的图形是（）

A、等边三角形 B、正方形 C、圆 D、平行四边形

查看试题解析
3. 如图，是由几个相同的小正方形搭成几何体的左视图，这几个几何体的摆搭方式可能是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式计算正确的是（）

A、 $a + 2 a^{2} = 3 a^{3}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $(a b)^{3} = a^{3} b^{3}$

查看试题解析
5. 在函数 $y = \frac{\sqrt{x + 5}}{x}$ 中，自变量x的取值范围是（）

A、 $x > 0$ B、 $x \geq - 5$ C、 $x \geq - 5$ 且 $x \neq 0$ D、 $x \geq 0$

查看试题解析
6. 如果关于x的不等式组 ${\begin{array}{l} x > a + 2 \\ x < 3 a - 2 \end{array}$ 无解，则a的取值范围是（）

A、a＜2 B、a＞2 C、a≥2 D、a≤2

查看试题解析
7. 如图，在方格纸上建立的平面直角坐标系中，将 $R t △ A B C$ 绕点C按顺时针方向旋转 $90 °$ ，得到 $R t △ F E C$ ，则点A的对应点F的坐标是（　　）

A、 $(- 1 ， 1)$ B、 $(- 1 ， 2)$ C、 $(1 ， 2)$ D、 $(2 ， 1)$

查看试题解析
8. 将含有 $30 °$ 的三角板 $A B C$ 按如图所示放置，点A在直线 $D E$ 上，其中 $∠ B A D = 15 °$ ，分别过点B，C作直线 $D E$ 的平行线 $F G$ ， $H I$ ，点B到直线 $D E$ ， $H I$ 的距离分别为 $h_{1}$ ， $h_{2}$ ，则 $\frac{h_{1}}{h_{2}}$ 的值为（）

A、1 B、 $\sqrt{3} - 1$ C、 $\sqrt{2} - 1$ D、 $\frac{\sqrt{6} - 2}{2}$

查看试题解析
9. 下列图形中，能确定 $∠ 1 > ∠ 2$ 的是（）

A、 B、 C、 D、

查看试题解析
10. 若 $A (- \frac{3}{4} ， y_{1})$ ， $B (- \frac{5}{4} ， y_{2})$ ， $C (\frac{1}{4} ， y_{3})$ 为二次函数 $y = x^{2} + 4 x - 5$ 的图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
11. 化简 $(9 - x^{2}) \div \frac{x^{2} - 3 x}{x}$ 的结果是（）

A、 $x + 3$ B、 $- x - 3$ C、 $\frac{1}{x + 3}$ D、 $- \frac{1}{x + 3}$

查看试题解析
12. 若关于x的一元二次方程x²－x+m＝0有两个不相等的实数根，则m的值可能是（）

A、0 B、1 C、2 D、2021

查看试题解析
13. 将抛物线C₁： $y = x^{2} + 4 x + 3$ 沿x轴对称后，向右平移3个单位长度，再向下平移3个单位长度，得到抛物线C₂ ．若抛物线C₁的顶点为A，点B是抛物线C₂与y轴的交点，O为坐标原点，则△AOB的面积为（　　）

A、1 B、2 C、3 D、4

查看试题解析
14. 如图，正方形 $A B C D$ 的对角线相交于点O， $R t △ O E F$ 绕点O旋转，在旋转过程中，两个图形重叠部分的面积是正方形面积的（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
15. 如图， $A B$ 是 $⊙ O$ 的弦， $O E ⊥ A B$ ， $E O$ 的延长线交 $⊙ O$ 于点 $F$ ，若 $E F = 8$ ， $s i n A = \frac{3}{5}$ ，则 $A B$ 长为（）

A、3 B、4 C、5 D、8

查看试题解析
16. $《$ 九章算术 $》$ 记载“今有邑方不知大小，各中开门．出北门三十步有木，出西门七百五十步见木．问邑方有几何？”意思是：如图，点M、点N分别是正方形 $A B C D$ 的边 $A D$ 、 $A B$ 的中点， $M E ⊥ A D$ ， $N F ⊥ A B$ ， $E F$ 过点A，且 $M E = 80$ 步， $N F = 245$ 步，则正方形的边长为（）

A、 $140$ 步 B、 $150$ 步 C、 $280$ 步 D、 $300$ 步

查看试题解析

二、填空题

17. 分解因式： $12 x y^{2} - 3 x =$ ．

查看试题解析
18. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ， P为 $A B$ 上一点，连接 $P A ， P E$ ，则 $∠ A P E$ 的度数为．

查看试题解析
19. 如图，过原点O的直线与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图像交于点A、P，过点P作x轴的垂线，点B为垂足，连接AB，若△ABP的面积是5，则 $k =$ ．

查看试题解析

三、解答题

20. 解方程： $x^{2} - 12 x = - 32$ ．

查看试题解析
21. 已知： $A C$ 与 $B D$ 交于点O， $A B = C D$ ， $A D = C B$ ．求证： $O D = O B$ $($ 规范证明过程 $)$
证明：在 $△ A B D$ 和 $△ C D B$ 中，
${\begin{array}{l} \underline{▲} \\ \underline{▲} \\ \underline{▲} \end{array}$
$∴ △ A B D ≌ △ C D B$        ▲
$∴ ∠$        ▲        $= ∠$         ▲
在 $△ A O D$ 和 $△ C O B$ 中，
${\begin{array}{l} \underline{▲} \\ \underline{▲} \\ \underline{▲} \end{array}$
$∴ △ A O D ≌ △ C O B$        ▲
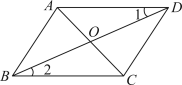
$∴ O D = O B$ ．

查看试题解析
22. 中学生上网现象越来越受到社会的关注，小记者小慧随机调查了某校若干学生和家长对上网现象的看法制作了如下的统计图1和2.请根据相关信息，解答或补全下列问题.

(1)、补全图1；

(2)、求图2中表示家长“赞成”的圆心角的度数；

(3)、该校共有1600名学生，请你估计这所中学的所有学生中，对上网持“反对”态度的有多少名？

查看试题解析
23. 如图1， $O P$ 是 $∠ M O N$ 的平分线，请你利用该图形画一对以 $O P$ 所在直线为对称轴的全等三角形，并将添加的全等条件标注在图上．
请你参考这个作全等三角形的方法，解答下列问题：
①如图2，在 $△ A B C$ 中， $∠ A C B$ 是直角， $∠ B = 60 °$ ， $A D$ 、 $C E$ 分别是 $∠ B A C$ 和 $∠ B C A$ 的平分线， $A D$ 、 $C E$ 相交于点F，求 $∠ E F A$ 的度数；
②在①的条件下，请判断 $F E$ 与 $F D$ 之间的数量关系，并说明理由；
③如图3，在 $△ A B C$ 中，如果 $∠ A C B$ 不是直角，而①中的其他条件不变，试问在②中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

查看试题解析
24. 如图，抛物线 $y = \frac{1}{2} x^{2} - x + a$ 与x轴交于点A、B，与y轴交于点C，其顶点纵坐标为-2．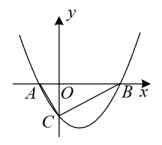

(1)、求a的值；

(2)、求A，B两点的坐标；

(3)、以 $A C$ ， $C B$ 为一组邻边作 $▱ A C B D$ ，则点D关于x轴的对称点 $D_{1}$ 是否在该抛物线上？请说明理由．

查看试题解析
25. 某班级同学从学校出发去白鹿原研学旅行，一部分坐大客车先出发，余下的几人 $20 m i n$ 后乘坐小轿车沿同一路线出行，大客车中途停车等候， $5 m i n$ 后小轿车赶了上来，大客车随即开动，以出发时速度的 $\frac{10}{7}$ 继续行驶，小轿车保持原速度不变，最终两车相继到达了景点入口，两车距学校的路程S(单位：km)和行驶时间t(单位：min之间的函数关系如图所示，请结合图象解决下列问题．

(1)、求大客车在途中等候时距学校的路程有多远？

(2)、在小轿车到达景点入口时，大客车离景点入口还有多远？

查看试题解析
26. 如图，在∠DAM内部作Rt△ABC，AB平分∠DAM，∠ACB＝90°，AB＝10，AC＝8，点N为BC的中点，动点E由A点出发，沿AB运动，速度为每秒5个单位，动点F由A点出发，沿AM运动，速度为每秒8个单位，当点E到达点B时，两点同时停止运动，过A、E、F作⊙O．

(1)、判断△AEF的形状为，并判断AD与⊙O的位置关系为；

(2)、求t为何值时，EN与⊙O相切，求出此时⊙O的半径，并比较半径与劣弧 $\overset{⌢}{A E}$ 长度的大小；

(3)、直接写出△AEF的内心运动的路径长为；（注：当A、E、F重合时，内心就是A点）

(4)、直接写出线段EN与⊙O有两个公共点时，t的取值范围为．
（参考数据：sin37°＝ $\frac{3}{5}$ ， tan37°＝ $\frac{3}{4}$ ， tan74°≈ $\frac{24}{7}$ ， sin74°≈ $\frac{24}{25}$ ， cos74°≈ $\frac{7}{25}$ ）

查看试题解析