河北省邯郸市武安市2023年中考数学一模试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 若 , 则( )内应填的数是( ).A、4 B、5 C、7 D、82. 如图,在三角形纸片中, , 把沿翻折 , 若点B落在点C的位置,则线段( ).
 A、是边上的中线 B、是边上的高 C、是的平分线 D、以上三种都成立3. 下列式子中计算结果与相等的是( ).A、 B、 C、 D、4. 下列等式正确的是( )A、 B、 C、 D、5. 如图,已知在中, , 若沿图中虚线剪去 , 则的度数是( ).
A、是边上的中线 B、是边上的高 C、是的平分线 D、以上三种都成立3. 下列式子中计算结果与相等的是( ).A、 B、 C、 D、4. 下列等式正确的是( )A、 B、 C、 D、5. 如图,已知在中, , 若沿图中虚线剪去 , 则的度数是( ). A、 B、 C、 D、6. 5G是第五代移动通信技术,应用5G网络下载一个1000的文件只需要 , 下载5个1000的文件需要的时间用科学记数法表示应为( ).A、 B、 C、 D、7. 如图,该长方体是由下面四个小几何体粘成的,那么图中第四部分对应的几何体是( ).
A、 B、 C、 D、6. 5G是第五代移动通信技术,应用5G网络下载一个1000的文件只需要 , 下载5个1000的文件需要的时间用科学记数法表示应为( ).A、 B、 C、 D、7. 如图,该长方体是由下面四个小几何体粘成的,那么图中第四部分对应的几何体是( ). A、
A、 B、
B、 C、
C、 D、
D、 8. 根据图中所给的边长及角度,下列四边形中,一定可以判定为平行四边形的是( ).A、
8. 根据图中所给的边长及角度,下列四边形中,一定可以判定为平行四边形的是( ).A、 B、
B、 C、
C、 D、
D、 9. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、210. 如图是个一不倒的主视图,不倒翁的圆形脸恰好与帽子边沿 , 分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若 , 则的度数为( ).
9. 已知两个不等于0的实数a、b满足 , 则等于( )A、 B、 C、1 D、210. 如图是个一不倒的主视图,不倒翁的圆形脸恰好与帽子边沿 , 分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若 , 则的度数为( ). A、 B、 C、 D、11. 已知等腰三角形纸片 , , . 现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).两名同学提供了如下方案:
A、 B、 C、 D、11. 已知等腰三角形纸片 , , . 现要将其剪成三张小纸片,使每张小纸片都是等腰三角形(不能有剩余).两名同学提供了如下方案:方案Ⅰ
方案Ⅱ
如图1,①分别作 , 的垂直平分线,交于点P;
②选择 , , .
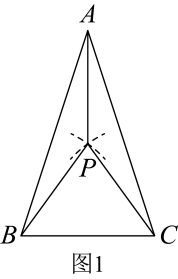
如图2,①以点B为圆心,长为半径画弧,交于点D,交于点E;
②连接 , .
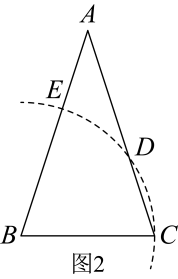
对于方案Ⅰ、Ⅱ,说法正确的是( ).
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行12. 初三年级甲、乙、丙、丁四个级部举行了知识竞赛,如图,平面直角坐标系中,x轴表示级部参赛人数,y轴表示竞赛成绩的优秀率(该级部优秀人数与该级部参加竞赛人数的比值),其中描述甲、丁两个级部情况的点恰好在同一个反比例函数的图象上,则这四个级部在这次知识竞赛中成绩优秀人数的多少正确的是( ) A、甲乙丙丁 B、丙甲丁乙 C、甲丁乙丙 D、乙甲丁丙13. 用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )
A、甲乙丙丁 B、丙甲丁乙 C、甲丁乙丙 D、乙甲丁丙13. 用四个螺丝将四条不可弯曲的本条围成一个木框(形状不限),不记螺丝大小,其中相邻两螺丝之间的距离依次为3,4,5,7.且相邻两本条的夹角均可调整,若调整木条的夹角时不破坏此木框,则任意两个螺丝之间的最大距离是( )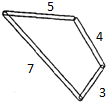 A、6 B、7 C、8 D、914. 已知一组数据1,2,3,4,5,a,b的平均数是4,若该组数据的中位数小于4,则a的值可能是( )A、7 B、8 C、9 D、1015. 《算法统宗》中记载了一个“李白沽酒”的故事,诗云:“今携一壶酒,游春郊外走,逢朋加一倍,入店饮半斗,相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友后,李白正好喝光了壶中的酒,请问各位,壶中原有( )升酒.A、5 B、 C、 D、16. 如图,在中, , , , , 动点P在边上,点P关于 , 的对称点分别为点E,F,连接 , 交 , 分别为点M,N.
A、6 B、7 C、8 D、914. 已知一组数据1,2,3,4,5,a,b的平均数是4,若该组数据的中位数小于4,则a的值可能是( )A、7 B、8 C、9 D、1015. 《算法统宗》中记载了一个“李白沽酒”的故事,诗云:“今携一壶酒,游春郊外走,逢朋加一倍,入店饮半斗,相逢三处店,饮尽壶中酒.试问能算士,如何知原有.”(注:古代一斗是10升)译文:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友后,李白正好喝光了壶中的酒,请问各位,壶中原有( )升酒.A、5 B、 C、 D、16. 如图,在中, , , , , 动点P在边上,点P关于 , 的对称点分别为点E,F,连接 , 交 , 分别为点M,N.甲:我发现线段的最大值为2,最小值为;
乙:我连接 , , 发现一定为钝角三角形.
则下列判断正确的是( )
 A、甲对乙对 B、甲对乙错 C、甲错乙对 D、甲错乙错
A、甲对乙对 B、甲对乙错 C、甲错乙对 D、甲错乙错二、填空题
-
17. 如图,在水平地面上的甲、乙两个区域分别由若干个大小完全相同的正三角形瓷砖组成,琪琪在甲、乙两个区域内分别随意抛一个小球,P(甲)表示小球停留在甲区域中灰色部分的概率,P(乙)表示小球停留在乙区域中灰色部分的概率,则P(甲)P(乙).(选镇“>”“<”或“=”)
 18. 如图,在正方形中,P,H分别为和上的点,与交于点E, .
18. 如图,在正方形中,P,H分别为和上的点,与交于点E, . (1)、判断与是否互相垂直;(选填“是”或“否”)(2)、若正方形的边长为4, , 则线段的长为 .19. 《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:
(1)、判断与是否互相垂直;(选填“是”或“否”)(2)、若正方形的边长为4, , 则线段的长为 .19. 《乌鸦喝水》的故事我们都听过,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题: (1)、放入一个小球水面升高 , 放入一个大球水面升高;(2)、如果放入个球且使水面恰好上升到 , 应放入大球个.
(1)、放入一个小球水面升高 , 放入一个大球水面升高;(2)、如果放入个球且使水面恰好上升到 , 应放入大球个.三、解答题
-
20. 已知两个数-4和a(a为负整数).
 (1)、设整式的值为P.当时,求P的值;(2)、已知-4,a,5的和的取值范围如图所示,求a的值.21. 某校360名学生参加植树活动,要求每人植树3~6棵,活动结束后随机抽查了20名学生每人的植树情况,并分为四种类型:A:3棵;B:4棵;C:5棵;D:6棵.根据各类型对应的人数绘制了如图所示的扇形统计图和尚来完成的条形统计图.请解答下列问题:
(1)、设整式的值为P.当时,求P的值;(2)、已知-4,a,5的和的取值范围如图所示,求a的值.21. 某校360名学生参加植树活动,要求每人植树3~6棵,活动结束后随机抽查了20名学生每人的植树情况,并分为四种类型:A:3棵;B:4棵;C:5棵;D:6棵.根据各类型对应的人数绘制了如图所示的扇形统计图和尚来完成的条形统计图.请解答下列问题:植树人数扇形统计图 植树人数条形统计图
 (1)、将条形统计图补充完整;(2)、在求这20名学生每人植树量的平均数时,嘉琪是这样分析的:
(1)、将条形统计图补充完整;(2)、在求这20名学生每人植树量的平均数时,嘉琪是这样分析的:第一步:求平均数的公式是;
第二步:在该问题中, , , , , ;
第三步:(棵).
①已知嘉琪的分析是错误的,他错在第几步?
②请你帮他计算出正确的平均数,并估计这360名学生共植树多少棵.
22. 新定义:如果a,b都是非零整数,且 , 那么就称a是“4倍数”.(1)、验证:嘉嘉说:是“4倍数”,琪琪说:也是“4倍数”,判断他们谁说得对?(2)、证明:设三个连续偶数的中间一个数是(n是整数),写出它们的平方和,并说明它们的平方和是“4倍数”.23. 如图,在平面直角坐标系中,线段的两个端点坐标分别为 , , 直线l的解析式为 , 点C的坐标为 . (1)、若直线l经过点C关于线段的对称点D,求直线l的解析式;(2)、在(1)的条件下,若将直线l向右平移n个单位长度,且平移后的直线经过线段的中点M,求n的值;(3)、直线经过点C,若这条直线与线段有交点(包含M,B两点),请直接写出k的取值范围.24. 如图,点P是△ABC内一点, , 垂足为点D,将线段PD绕点P顺时针旋转90°得到扇形DPE,过点E作交AB于点M,连接PM,与交于点F,过点P作交BC于点N.
(1)、若直线l经过点C关于线段的对称点D,求直线l的解析式;(2)、在(1)的条件下,若将直线l向右平移n个单位长度,且平移后的直线经过线段的中点M,求n的值;(3)、直线经过点C,若这条直线与线段有交点(包含M,B两点),请直接写出k的取值范围.24. 如图,点P是△ABC内一点, , 垂足为点D,将线段PD绕点P顺时针旋转90°得到扇形DPE,过点E作交AB于点M,连接PM,与交于点F,过点P作交BC于点N. (1)、求证:;(2)、已知 , .
(1)、求证:;(2)、已知 , .①通过计算比较线段PN和哪个长度更长;
②计算图中阴影部分的面积(结果保留).
25. 如图,x轴上依次有A,B,D,C四个点,且 , 从点A处向右上方沿抛物线发出一个带光的点 (1)、求点A的横坐标,且在图中补画出y轴;(2)、通过计算说明点P是否会落在点C处,并补全抛物线;(3)、求抛物线的顶点坐标和对称轴;(4)、在x轴上从左到右有两点E,F,且 , 从点F向上作轴,且在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边(包括端点)上,直接写出点G横坐标的最大值与最小值.26. 有两张全等的等腰直角三角形纸片和 , , .
(1)、求点A的横坐标,且在图中补画出y轴;(2)、通过计算说明点P是否会落在点C处,并补全抛物线;(3)、求抛物线的顶点坐标和对称轴;(4)、在x轴上从左到右有两点E,F,且 , 从点F向上作轴,且在沿x轴左右平移时,必须保证沿抛物线下落的点P能落在边(包括端点)上,直接写出点G横坐标的最大值与最小值.26. 有两张全等的等腰直角三角形纸片和 , , . (1)、如图1,若点F在边的中点M处, , 将沿射线方向平移 , 当四边形是菱形时,求a的值;(2)、若将图1中的以点F为旋转中心,按逆时针方向旋转一定角度,交于点G,交于点H,如图2,发现 , 请你证明这个结论;(3)、若将图1中的沿射线方向平移 , 接着以点F为旋转中心,按顺时针方向旋转至经过点C时,交于点G,如图3,求出此时两张等腰直角三角形纸片重叠部分的面积.
(1)、如图1,若点F在边的中点M处, , 将沿射线方向平移 , 当四边形是菱形时,求a的值;(2)、若将图1中的以点F为旋转中心,按逆时针方向旋转一定角度,交于点G,交于点H,如图2,发现 , 请你证明这个结论;(3)、若将图1中的沿射线方向平移 , 接着以点F为旋转中心,按顺时针方向旋转至经过点C时,交于点G,如图3,求出此时两张等腰直角三角形纸片重叠部分的面积.