广东省肇庆市封开县2023年一模数学试卷
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 计算:( )A、 B、- C、 D、52. 在下列平面图形中,是中心对称图形的是( )A、平行四边形 B、等腰直角三角形 C、等边三角形 D、角3. 2022年全国教育事业统计主要结果发布,统计数据显示,全国共有各级各类学校万52.93万所,将52.93万用科学记数法表示应为( )A、 B、 C、 D、4. 已知:如图 , 是的两条半径,且 , 点在上,则的度数为( )
 A、 B、 C、 D、5. 如图,是由个相同的小正方体组成的几何体,其左视图是( )
A、 B、 C、 D、5. 如图,是由个相同的小正方体组成的几何体,其左视图是( )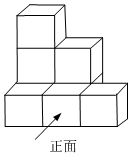 A、
A、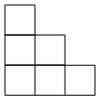 B、
B、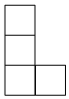 C、
C、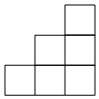 D、
D、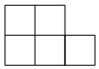 6. 不透明的袋中装有只有颜色不同的10个小球,其中6个红色,4个白色,从袋中任意摸出一个球是红球的概率是( ).A、 B、 C、 D、7. 如图,是由绕点O顺时针旋转后得到的图形,若的度数为 , 则的度数是( )
6. 不透明的袋中装有只有颜色不同的10个小球,其中6个红色,4个白色,从袋中任意摸出一个球是红球的概率是( ).A、 B、 C、 D、7. 如图,是由绕点O顺时针旋转后得到的图形,若的度数为 , 则的度数是( ) A、 B、 C、 D、8. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 对于抛物线 , 下列判断正确的是( )A、顶点 B、抛物线向左平移个单位长度后得到 C、抛物线与y轴的交点是 D、当时,y随x的增大而增大10. 如图,在矩形ABCD中,AC为对角线, , , 以B为圆心,AB长为半径画弧,交AC于点M,交BC于点N,则阴影部分的面积为( )
A、 B、 C、 D、8. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 对于抛物线 , 下列判断正确的是( )A、顶点 B、抛物线向左平移个单位长度后得到 C、抛物线与y轴的交点是 D、当时,y随x的增大而增大10. 如图,在矩形ABCD中,AC为对角线, , , 以B为圆心,AB长为半径画弧,交AC于点M,交BC于点N,则阴影部分的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 已知正n边形的一个外角为 , 则n=13. 如图,在△ABC中,∠A=50°,∠B=80°,观察图中尺规作图的痕迹,则∠DCE的度数为 .
 14. 已知 , 那么的值为 .15. 如图,正方形中,点E是的中点,将正方形沿翻折,点B落在点F处,延长交于点P,若 , 则的长为 .
14. 已知 , 那么的值为 .15. 如图,正方形中,点E是的中点,将正方形沿翻折,点B落在点F处,延长交于点P,若 , 则的长为 .
三、解答题
-
16. 计算: .17. 解不等式组:18. 如图,点A、D、C、F在同一条直线上, ,

求证:
(1)、;(2)、 .19. 先化简,再求值: , 其中 .20. 某校组织全校学生进行了“航天知识竞赛”,教务处从中随机抽取了n名学生的竞赛成绩(满分100分,每名学生的成绩记为x分)分成如表中四组,并得到如下不完整的频数分布表、频数分布直方图和扇形统计图.根据图中信息,解答下列问题:分组
频数
A:
a
B:
18
C:
24
D:
b
 (1)、n的值为 , a的值为 , b的值为;(2)、请补全频数分布直方图 , 并计算扇形统计图中表示“C”的圆心角的度数为°;(3)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机为抽取两名宣讲航天知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.21. 我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.(1)、篮球和排球各购进了多少个(列方程组解答)?(2)、因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?
(1)、n的值为 , a的值为 , b的值为;(2)、请补全频数分布直方图 , 并计算扇形统计图中表示“C”的圆心角的度数为°;(3)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机为抽取两名宣讲航天知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.21. 我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.(1)、篮球和排球各购进了多少个(列方程组解答)?(2)、因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?

