广东省佛山市禅城区2023年中考数学模拟试卷

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $x^{3} + x^{3} = x^{9}$ B、 $3 x - x = 2$ C、 $(x y)^{2} = x^{2} y^{2}$ D、 $(x^{3})^{4} = x^{7}$

查看试题解析
2. 连接正八边形的三个顶点，得到如图所示的图形，下列说法错误的是（）

A、四边形ABCH与四边形EFGH的周长相等 B、连接HD，则HD平分∠CHE C、整个图形不是中心对称图形 D、 $△ C E H$ 是等边三角形

查看试题解析
3. 下列实数： $0$ ， $π$ ， $\sqrt{5}$ ， $- 1$ ，其中最大的实数是（　　）

A、 $0$ B、 $π$ C、 $\sqrt{5}$ D、 $- 1$

查看试题解析
4. 如图，两条平行线a，b被第三条直线c所截．若 $∠ 2 = 56 °$ ，则 $∠ 1$ 的度数为（）

A、 $120 °$ B、 $112 °$ C、 $124 °$ D、 $56 °$

查看试题解析
5. 如图所示的物体中，一样的为（）

A、(1)与(2) B、(1)与(3) C、(1)与(4) D、(2)与(3)

查看试题解析
6. 春节期间，某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开放海产品的运输业务，两货运公司的收费项目及收费标准如下表所示．已知运输路程为140千米，汽车和火车的速度分别为70千米/时，100千米/时．
运输工具
运输费/（元/吨·千米）
冷藏费/（元/吨·时）
过路费/元
卸载及管理费/元
汽车
2
5
200
0
火车
1.8
5
0
1750
下列说法正确的是（）

A、当运输货物质量为60吨，选择汽车 B、当运输货物质量大于50吨，选择汽车 C、当运输货物质量小于50吨，选择火车 D、当运输货物质量大于50吨，选择火车

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c$ 的图像如图所示，有下列结论：① $a ＞ 0$ ；② $b^{2} - 4 a c$ ＞0；③ $4 a + b = 0$ ；④不等式 $a x^{2} + （ b - 1 ） x + c$ ＜0的解集为1≤x＜3，正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. “天上星星有几颗，7后跟上22个0”，这是国际天文学联合大会上宣布的消息，用科学记数法表示宇宙空间星星颗数为（）．

A、 $700 \times 10^{20}$ B、 $7 \times 10^{23}$ C、 $0.7 \times 10^{23}$ D、 $7 \times 10^{22}$

查看试题解析
9. 如图，在菱形ABCD中，AE⊥BC于E，将△ABE沿AE所在直线翻折得△AEF，若AB＝2，∠B＝45°，则△AEF与菱形ABCD重叠部分（阴影部分）的面积为（）.

A、2 B、 $2 - \sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $2 \sqrt{2} - 2$

查看试题解析
10. 在样本方差的计算公式S²＝ $\frac{1}{10}$ [（x₁-20）²+（x₂-20）²+…+（x₁₀-20）²]中，数字10和20分别表示样本的（　　）

A、容量和方差 B、标准差和平均数 C、容量和平均数 D、平均数和容量

查看试题解析

二、填空题

11. 因式分解： $x^{2} y - 5 x y + 6 y =$ ．

查看试题解析
12. 已知 $△ A B C ∽ △ A_{1} B_{1} C_{1}$ ，顶点A、B、C分别与 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 对应，若 $∠ A = 40^{\circ}$ ， $∠ C = 60^{\circ}$ ，则 $∠ B_{1} =$ 度．

查看试题解析
13. 若 $\sqrt{x - 1}$ 与 $| 2 x + y - 6 |$ 互为相反数，则 $(x + y)^{2}$ 的平方根是．

查看试题解析
14. 如图，在某中学操场内，测得看台 $B D$ 的高为 $3 m$ ，坡角 $∠ B A D$ 为 $30 °$ ，从同一列上的第一排的点A和最后一排的点B处测得旗杆顶部的仰角分别为 $60 °$ 和 $30 °$ ，旗杆底部点O与第一排点A在同一水平面上，则旗杆 $C O$ 的高度为 $m$ ．

查看试题解析
15. 如图，△ABC与△DCE都是等边三角形，B，C，E三点在同一条直线上，若AB=6，∠BAD=150°，则DE的长为．

查看试题解析

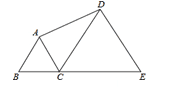
三、解答题

16. 跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售．若每个甲种零件的进价比每个乙种零件的进价少2元，且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同．

(1)、求每个甲种零件、每个乙种零件的进价分别为多少元？

(2)、若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个，购进两种零件的总数量不超过95个，该五金商店每个甲种零件的销售价格为12元，每个乙种零件的销售价格为15元，则将本次购进的甲、乙两种零件全部售出后，可使销售两种零件的总利润（利润＝售价－进价）超过371元，通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案？请你设计出来．

查看试题解析
17. 反比例函数 $y = \frac{2}{x}$ 的图象与一次函数 $y = k x + b$ 的图象交于点 $A (m ， 2)$ ，点 $B (- 2 ， n)$ ，一次函数图象与y轴的交点为C．

(1)、求一次函数的解析式；

(2)、求 $△ A O C$ 的面积．

查看试题解析
18. 如图 $1$ ，对于平面内小于等于 $90 °$ 的 $∠ M O N$ ，我们给出如下定义：若点P在 $∠ M O N$ 的内部或边上，作 $P E ⊥ O M$ 于点 $E$ ， $P F ⊥ O N$ 于点F，则将 $P E + P F$ 称为点P与 $∠ M O N$ 的“点角距”，记作 $d (∠ M O N ， P)$ ．如图 $2$ ，在平面直角坐标系 $x O y$ 中，x、y正半轴所组成的角为 $∠ x O y$ ．

(1)、已知点 $A (5 ， 0)$ 、点 $B (3 ， 2)$ ，则 $d (∠ x O y ， A) =$ ， $d (∠ x O y ， B) =$ ．

(2)、若点P为 $∠ x O y$ 内部或边上的动点，且满足 $d (∠ x O y ， P) = 5$ ，在图 $2$ 中画出点P运动所形成的图形．

(3)、如图 $3$ ，在平面直角坐标系 $x O y$ 中，抛物线 $y = - \frac{1}{2} x^{2} + m x + n$ 经过 $A (5 ， 0)$ 与点 $D (3 ， 4)$ 两点，点Q是A、D两点之间的抛物线上的动点(点Q可与A、D两点重合)，求当 $d (∠ x O D ， Q)$ 取最大值时点Q的坐标．

查看试题解析
19. 在一节数学课上，刘老师请同学心里想一个非零的有理数，然后把这个数按照下面的程序进行计算后，刘老师立刻说出计算结果．

(1)、小明同学心里想的数是8，列出了下面的算式，请你计算出最后的结果： $[(8 + 2)^{2} - (8 - 2)^{2}] \times (- 25) \div 8$ ；

(2)、小明又试了几个数进行计算，发现结果都相等，于是小明把心里想的这个数记作 $a (a \neq 0)$ ，并按照程序通过计算进行验证，请你写出这个验证过程．

查看试题解析
20. 如图，四边形ABCD为菱形，已知A（3，0），B（0， 4）．

(1)、求点C的坐标；

(2)、求经过点C，D两点的一次函数的解析式．

查看试题解析
21. 甲口袋中装有 $3$ 个相同的小球，它们分别写有数字 $1$ ， $2$ ， $3$ ；乙口袋中装有 $3$ 个相同的小球，它们分别写有数字 $4$ ， $5$ ， $6$ ．从两个口袋中各随机取出 $1$ 个小球．

(1)、采用树状图法（或列表法）列出所有可能的结果；

(2)、求取出的两个小球标号都是奇数的概率．

查看试题解析
22. 如图，四边形 $A B C D$ 中，连接 $A C$ ， $A C = A D$ ，以 $A C$ 为直径的 $⊙ O$ 过点B，交 $C D$ 于点E，过点E作 $E F ⊥ A D$ 于点F．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、若 $∠ B A C = ∠ D A C = 30 °$ ， $B C = 2$ ，求 $\overset{⌢}{B C E}$ 的长．（结果保留 $π$ ）

查看试题解析
23.

(1)、【操作体验】用一张矩形纸片折等边三角形．

第一步，对折矩形纸片 $A B C D$ （ $A B > B C$ ）（图 $①$ ），使 $A B$ 与 $D C$ 重合，得到折痕 $E F$ ，把纸片展平（图②）．

第二步，如图③，再一次折叠纸片，使点C落在 $E F$ 上的P处，并使折痕经过点B，得到折痕 $B G$ ，折出 $P B$ ， $P C$ ，得到 $△ P B C$ ．

请证明△PBC是等边三角形．

(2)、【数学思考】
如图④，小明画出了图③的矩形 $A B C D$ 和等边三角形 $P B C$ ．他发现，在矩形 $A B C D$ 中把 $△ P B C$ 经过图形变化，可以得到图⑤中的更大的等边三角形．请描述图形变化的过程．

(3)、【问题解决】
已知矩形一边长为 $3 c m$ ，另一边长为 $a c m$ ．对于每一个确定的 $a$ 的值，在矩形中都能画出最大的等边三角形．请画出不同情形的示意图，并写出对应的 $a$ 的取值范围．

查看试题解析

运输工具	运输费/（元/吨·千米）	冷藏费/（元/吨·时）	过路费/元	卸载及管理费/元
汽车	2	5	200	0
火车	1.8	5	0	1750