安徽省合肥市新站高新区2023年九年级第一次模拟检测数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 二次函数图象的顶点坐标是( )A、 B、 C、 D、2. 下列图形中,主视图和左视图一样的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,中, , 且 , 则的值是( )
3. 如图,中, , 且 , 则的值是( ) A、 B、 C、 D、4. 一个钢球沿坡角31°的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( )
A、 B、 C、 D、4. 一个钢球沿坡角31°的斜坡向上滚动了5米,此时钢球距地面的高度是(单位:米)( ) A、 B、 C、 D、5. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 和 ,则这一杠杆的动力 和动力臂 之间的函数图象大致是( )
A、 B、 C、 D、5. 阿基米德说:“给我一个支点,我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为 和 ,则这一杠杆的动力 和动力臂 之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、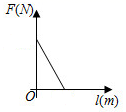 D、
D、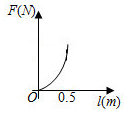 6. 若 , 则的值等于( )A、 B、 C、 D、7. 如图,在中, , D是的中点, , , 则等于( )
6. 若 , 则的值等于( )A、 B、 C、 D、7. 如图,在中, , D是的中点, , , 则等于( ) A、 B、 C、 D、8. 如图,是的直径,弦交于点E,连接 . 若 , 则的度数是( )
A、 B、 C、 D、8. 如图,是的直径,弦交于点E,连接 . 若 , 则的度数是( ) A、 B、 C、 D、9. 如图,为等边三角形,平分 , , 点E为上动点,连接 , 则的最小值为( )
A、 B、 C、 D、9. 如图,为等边三角形,平分 , , 点E为上动点,连接 , 则的最小值为( ) A、1 B、 C、 D、210. 已知抛物线的图像经过第四象限,则m的取值范围是( )A、 B、 C、 D、
A、1 B、 C、 D、210. 已知抛物线的图像经过第四象限,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 若 , 且 , 则度.12. 如图,线段与相切于点B,线段与相交于点C, , , 则的半径长为 .
 13. 如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上, , 反比例函数的图象经过点B,若阴影部分面积为4,则k的值为 .
13. 如图,在平面直角坐标系中,矩形的顶点A在x轴上,顶点C在y轴上,矩形的边在上, , 反比例函数的图象经过点B,若阴影部分面积为4,则k的值为 .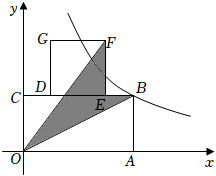 14. 如图,在边长为10的正方形中,M,N分别是、的中点,交于点E,连接 , 过点A作 , 垂足为F,延长分别交于G,D,求:
14. 如图,在边长为10的正方形中,M,N分别是、的中点,交于点E,连接 , 过点A作 , 垂足为F,延长分别交于G,D,求: (1)、(2)、
(1)、(2)、三、解答题
-
15. 计算:16. 如图,在平面直角坐标系中,的三个顶点坐标分别为、、
 (1)、以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的 .(2)、画出绕O点顺时针旋转后得到的 .(3)、直接写出点B所经过的路径长 .17. 已知抛物线的顶点在直线上(1)、求k的值;(2)、请判断抛物线与x轴交点的个数,并说明理由.18. 如图,在中,为直径,点B、C在上,交于点E()连接 , .
(1)、以原点O为位似中心,在第二象限内画出将放大为原来的2倍后的 .(2)、画出绕O点顺时针旋转后得到的 .(3)、直接写出点B所经过的路径长 .17. 已知抛物线的顶点在直线上(1)、求k的值;(2)、请判断抛物线与x轴交点的个数,并说明理由.18. 如图,在中,为直径,点B、C在上,交于点E()连接 , . (1)、求证:;(2)、若 , , 求的长.19. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.
(1)、求证:;(2)、若 , , 求的长.19. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.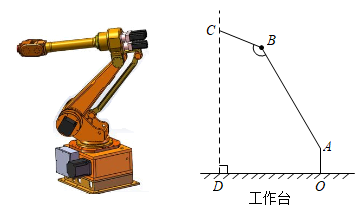 (1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )20. 如图,直线与双曲线交于 , 两点,连接 , .
(1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )20. 如图,直线与双曲线交于 , 两点,连接 , . (1)、求的面积;(2)、根据函数图象,直接写出不等式的解集是 .21. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图:
(1)、求的面积;(2)、根据函数图象,直接写出不等式的解集是 .21. 某中学积极落实国家“双减”教育政策,决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量,促进学生全面健康发展为优化师资配备,学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程(要求必须选修一门且只能选修一门)?”的随机问卷调查,并根据调查数据绘制了如下两幅不完整的统计图: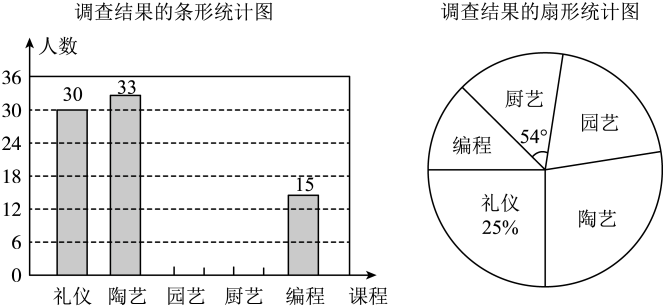
请结合上述信息,解答下列问题:
(1)、共有名学生参与了本次问卷调查;“陶艺”在扇形统计图中所对应的圆心角是度;(2)、补全调查结果条形统计图;(3)、小刚和小强分别从“礼仪”等五门校本课程中任选一门,请用列表法或画树状图法求出两人恰好选到同一门课程的概率.



