安徽省池州市2023年名校中考调研试卷(一)数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 在四个数2,0, , 中,比小的数是( )A、2 B、0 C、 D、2. 据《人民网》报道,在2022卡塔尔世界杯承担开、闭幕式等重要活动的卢塞尔球场是由中国铁建集团承建,其建筑面积为195000平方米.把数字“195000”用科学记数法表示为( )A、 B、 C、 D、3. 如图, , , 则( )
 A、 B、 C、 D、4. 如图所示的几何体的俯视图是( )
A、 B、 C、 D、4. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列计算结果正确的是( )A、 B、 C、 D、6. 下列选项中,最适宜采用全面调查(普查)方式的是( )A、检测神舟十五号飞船的零部件 B、调查某市中学生的视力状况 C、调查安徽省中学生的体育运动情况 D、调查一批节能灯的使用寿命7. 某产品的成本价为a元,销售价比成本价增加了 , 现因库存积压,按销售价的八折出售,那么该产品的实际售价为( )A、元 B、元 C、元 D、元8. 如图,正方形的边长为4,点P从点D出发,沿D→C→B→A路线运动.设点P经过的路程为x,的面积为y,则能大致反映y与x的函数关系的图象是( )
5. 下列计算结果正确的是( )A、 B、 C、 D、6. 下列选项中,最适宜采用全面调查(普查)方式的是( )A、检测神舟十五号飞船的零部件 B、调查某市中学生的视力状况 C、调查安徽省中学生的体育运动情况 D、调查一批节能灯的使用寿命7. 某产品的成本价为a元,销售价比成本价增加了 , 现因库存积压,按销售价的八折出售,那么该产品的实际售价为( )A、元 B、元 C、元 D、元8. 如图,正方形的边长为4,点P从点D出发,沿D→C→B→A路线运动.设点P经过的路程为x,的面积为y,则能大致反映y与x的函数关系的图象是( )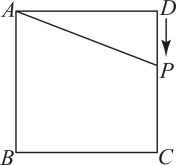 A、
A、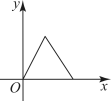 B、
B、 C、
C、 D、
D、 9. 如图,是的外接圆,是直径,过点C的切线交的延长线干点D,若 , , 则的半径长为( )
9. 如图,是的外接圆,是直径,过点C的切线交的延长线干点D,若 , , 则的半径长为( ) A、 B、 C、 D、10. 如图,在中, , , , 动点M,N分别在边 , 上则的最小值是( )
A、 B、 C、 D、10. 如图,在中, , , , 动点M,N分别在边 , 上则的最小值是( )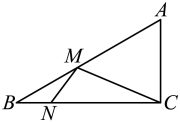 A、 B、 C、6 D、
A、 B、 C、6 D、二、填空题
-
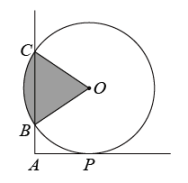
11. 计算: + = .12. 因式分解:13. 如图, , 与的一边相切于点P,与另一边相交于B,C两点,且 , , 则扇形的面积为
 14. 如图,已知四边形是正方形, , 点E为对角线上一动点,连接 , 过点E作 , 交射线于点F,以 , 为邻边作矩形 , 连接 .
14. 如图,已知四边形是正方形, , 点E为对角线上一动点,连接 , 过点E作 , 交射线于点F,以 , 为邻边作矩形 , 连接 .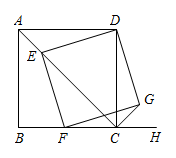 (1)、;(2)、若四边形的面积为5,则
(1)、;(2)、若四边形的面积为5,则三、解答题
-
15. 解不等式组:16. 如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均在格点(网格线的交点)上.
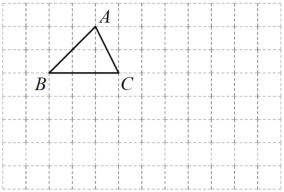
( 1 )将向右平移5个单位长度,向上平移1个单位长度得到 , 画出;
( 2 )将以点C为位似中心放大2倍得到 , 画出.
17. 观察下列式子:第1个等式: ,
第2个等式: ,
第3个等式: , …
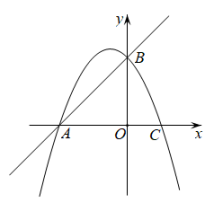
(1)、根据你发现的规律,请写出第5个等式:(2)、请写出第n个等式,并证明等式的正确性.18. 如图是置物架的侧面示意图,置物板与地面平行,斜支架与地面的夹角 , ;挡板与置物板的夹角 , . 求挡板顶端F到地面的距离.(参考数据: , , ) 19. 如图,直线与双曲线()交于点A,并与坐标轴分别交于点B,C.过点A作轴,交x轴于点D,连接 , 当的面积为4时,求线段的长.
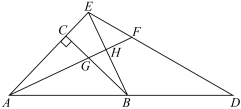
19. 如图,直线与双曲线()交于点A,并与坐标轴分别交于点B,C.过点A作轴,交x轴于点D,连接 , 当的面积为4时,求线段的长. 20. 如图,内接于半圆O,为直径,的平分线交于点F,交半圆O于点D,于点E,且交于点P,连接 .
20. 如图,内接于半圆O,为直径,的平分线交于点F,交半圆O于点D,于点E,且交于点P,连接 .
求证:
(1)、;(2)、点P是线段的中点.21. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”我市某中学响应号召,鼓励师生利用课余时间广泛阅读,该校文学社发起了“读书感悟•分享”比赛活动根据参赛学生的成绩划分为 , , , 四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;频数
频率
4
0.3
16
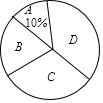 (1)、求 , 的值;(2)、求 等级对应扇形圆心角的度数;(3)、学校要从 等级的学生中随机选取2人参加市级比赛,求 等级中的学生小明被选中参加市级比赛的概率.
(1)、求 , 的值;(2)、求 等级对应扇形圆心角的度数;(3)、学校要从 等级的学生中随机选取2人参加市级比赛,求 等级中的学生小明被选中参加市级比赛的概率.