山东省济南市市中区2022年中考模拟测试数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
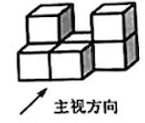
1. 的倒数是( )A、 B、 C、5 D、2. 如图所示的几何体是由7个相同的小正方体组成的立体图形, 则下列四个图形中是它的 俯视图的是( )
 A、
A、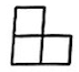 B、
B、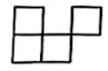 C、
C、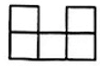 D、
D、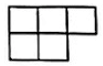 3. 据人民网5月20日电报道:中国森林生态系统年涵养水源量4947.66亿立方米,相当于12个三峡水库2009年蓄水至175米水位后库容量,将4947.66亿用科学记数法表示为()A、4.94766×1013 B、4.94766×1012 C、4.94766×1011 D、4.94766×10104. 如图,直线ab,∠1=50°,则∠2的度数是( )
3. 据人民网5月20日电报道:中国森林生态系统年涵养水源量4947.66亿立方米,相当于12个三峡水库2009年蓄水至175米水位后库容量,将4947.66亿用科学记数法表示为()A、4.94766×1013 B、4.94766×1012 C、4.94766×1011 D、4.94766×10104. 如图,直线ab,∠1=50°,则∠2的度数是( ) A、50° B、40° C、130° D、150°5. 下面的图形中,既是轴对称图形又是中心对称图形的是( ).A、
A、50° B、40° C、130° D、150°5. 下面的图形中,既是轴对称图形又是中心对称图形的是( ).A、 B、
B、 C、
C、 D、
D、 6. 下列计算正确的是( )A、 B、 C、 D、7.
6. 下列计算正确的是( )A、 B、 C、 D、7.如图,在平面直角坐标系中,A(﹣3,2)、B(﹣1,0)、C(﹣1,3),将
△ABC向右平移4个单位,再向下平移3个单位,得到△A1B1C1 , 点A、B、C的
对应点分别A1、B1、C1 , 则点A1的坐标为( )
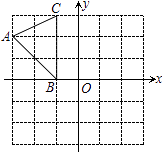 A、(3,﹣3) B、(1,﹣1) C、(3,0) D、(2,﹣1)8. 如图,四个带圆圈的数字,任取两个数字(既可以是相邻,也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①,②两数在相对位置上的概率是( )
A、(3,﹣3) B、(1,﹣1) C、(3,0) D、(2,﹣1)8. 如图,四个带圆圈的数字,任取两个数字(既可以是相邻,也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①,②两数在相对位置上的概率是( ) A、 B、 C、 D、9. 如图,反比例函数(k>0)与一次函数的图象相交于两点A( , ),B( , ),线段AB交y轴与C,当|- |=2且AC = 2BC时,k、b的值分别为( )
A、 B、 C、 D、9. 如图,反比例函数(k>0)与一次函数的图象相交于两点A( , ),B( , ),线段AB交y轴与C,当|- |=2且AC = 2BC时,k、b的值分别为( ) A、k= , b=2 B、k= , b=1 C、k= , b= D、k= , b=10. 如图,在中, , , 以A为圆心,任意长为半径画弧分别交于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结并延长交于点D,则下列说法中错误的是( )
A、k= , b=2 B、k= , b=1 C、k= , b= D、k= , b=10. 如图,在中, , , 以A为圆心,任意长为半径画弧分别交于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结并延长交于点D,则下列说法中错误的是( ) A、是的平分线 B、 C、点D在的中垂线上 D、11.
A、是的平分线 B、 C、点D在的中垂线上 D、11.某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
 A、8.1米 B、17.2米 C、19.7米 D、25.5米12. 在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣或x=1.其中正确的有( )
A、8.1米 B、17.2米 C、19.7米 D、25.5米12. 在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣或x=1.其中正确的有( )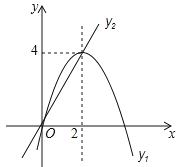 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 因式分解: .
14. 小球在如图6所示的地板上自由滚动,并随机停留在某块正方形的地砖上,则它停在白色地砖上的概率是. 15. 在等腰 中, 的对边分别为 ,已知 和 是关于 的方程 的两个实数根,则 的周长是 .16. 如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令 , .若 ,且S▱ABCD=36,则四边形FGEH的面积为 .
15. 在等腰 中, 的对边分别为 ,已知 和 是关于 的方程 的两个实数根,则 的周长是 .16. 如图,点E、F分别在平行四边形ABCD边BC和AD上(E、F都不与两端点重合),连结AE、DE、BF、CF,其中AE和BF交于点G,DE和CF交于点H.令 , .若 ,且S▱ABCD=36,则四边形FGEH的面积为 .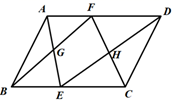 17. 把1~9这九个数填入3×3方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为 .
17. 把1~9这九个数填入3×3方格中,使其任意一行,任意一列及任意一条对角线上的数之和都相等,这样便构成了一个“九宫格”,它源于我国古代的“洛书”(图1),是世界上最早的“幻方”.图2是仅可以看到部分数值的“九宫格”,则的值为 . 18. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, , , 则= .
18. 如图,已知四边形ABCD,AC与BD相交于点O,∠ABC=∠DAC=90°, , , 则= .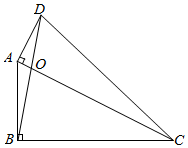
三、解答题
-
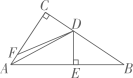
19.20. 已知关于x的分式方程 无解,关于y的不等式组 的整数解有且仅有3个,求n的取值范围.21. 如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC,求证:BD=DF.
 22. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
22. 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题: (1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.23. 如图①,在平面直角坐标系中,直线y=kx+b与x轴正半轴交于点A,与y轴负半轴交于点B,圆心P在x轴的正半轴上,已知AB=10,AP=
(1)、在这项调查中,共调查了多少名学生?(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;(3)、若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.23. 如图①,在平面直角坐标系中,直线y=kx+b与x轴正半轴交于点A,与y轴负半轴交于点B,圆心P在x轴的正半轴上,已知AB=10,AP= (1)、求点P到直线AB的距离;(2)、求直线y=kx+b的解析式;(3)、在图②中存在点Q,使得∠BQO=90°,连接AQ,请求出AQ的最小值.24. 某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.(1)、求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)(2)、商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?25. 若抛物线 ( 是常数, )与直线 都经过 轴上的一点 ,且抛物线 的顶点 在直线 上,则称此直线 与该抛物线 具有“一带一路”关系.此时,直线 叫做抛物线 的“带线”,抛物线 叫做直线 的“路线”.(1)、若直线 与抛物线 具有“一带一路”关系,求 的值;(2)、若某“路线” 的顶点在反比例函数 的图象上,它的“带线” 的解析式为 ,求此“路线” 的解析式;(3)、当常数 满足 时,请直接写出抛物线 : 的“带线” 与 轴, 轴所围成的三角形面积S的取值范围.26. 已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.
(1)、求点P到直线AB的距离;(2)、求直线y=kx+b的解析式;(3)、在图②中存在点Q,使得∠BQO=90°,连接AQ,请求出AQ的最小值.24. 某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.(1)、求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)(2)、商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?25. 若抛物线 ( 是常数, )与直线 都经过 轴上的一点 ,且抛物线 的顶点 在直线 上,则称此直线 与该抛物线 具有“一带一路”关系.此时,直线 叫做抛物线 的“带线”,抛物线 叫做直线 的“路线”.(1)、若直线 与抛物线 具有“一带一路”关系,求 的值;(2)、若某“路线” 的顶点在反比例函数 的图象上,它的“带线” 的解析式为 ,求此“路线” 的解析式;(3)、当常数 满足 时,请直接写出抛物线 : 的“带线” 与 轴, 轴所围成的三角形面积S的取值范围.26. 已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x. (1)、若点F恰好是AE的中点,求线段BD的长;(2)、若y= ,求y关于x的函数关系式,并写出它的定义域;(3)、当△ADE是以AD为腰的等腰三角形时,求线段BD的长.27. 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
(1)、若点F恰好是AE的中点,求线段BD的长;(2)、若y= ,求y关于x的函数关系式,并写出它的定义域;(3)、当△ADE是以AD为腰的等腰三角形时,求线段BD的长.27. 如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点. (1)、求出抛物线的解析式;(2)、在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)、点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 的值,并求出此时点M的坐标.
(1)、求出抛物线的解析式;(2)、在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;(3)、点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 的值,并求出此时点M的坐标.