山东省济南市莱芜区2022年中考模拟测数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. ﹣ 的绝对值是( )
A、﹣ B、 C、﹣5 D、52. 如图是某会展中心展出的一只紫砂壶,你认为是从上面看到的效果图是( ) A、
A、 B、
B、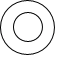 C、
C、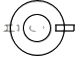 D、
D、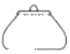 3. 第七次全国人口普查数据显示,诸暨市常住人口约为1220000人,这个数字1220000用科学记数法可表示为( )A、 B、 C、 D、4. 如图, , , ,则 的大小是( )
3. 第七次全国人口普查数据显示,诸暨市常住人口约为1220000人,这个数字1220000用科学记数法可表示为( )A、 B、 C、 D、4. 如图, , , ,则 的大小是( ) A、 B、 C、 D、5. 下列图形中,是轴对称图形的是( )A、
A、 B、 C、 D、5. 下列图形中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6.
6.如图:把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离AA′是( )
 A、 B、 C、1 D、7. 下列各式中,正确的是( )A、 B、 C、 D、8. 一班、二班各有m名学生,某次体能测试后,对测试成绩进行了整理和分析(成绩用x表示,单位:分),分成四个组:甲: ;乙: ;丙: ;丁: ,并绘制了下列统计图:
A、 B、 C、1 D、7. 下列各式中,正确的是( )A、 B、 C、 D、8. 一班、二班各有m名学生,某次体能测试后,对测试成绩进行了整理和分析(成绩用x表示,单位:分),分成四个组:甲: ;乙: ;丙: ;丁: ,并绘制了下列统计图:
已知一班在乙组中共有15名同学,他们的成绩分别为:
85,85,85,86,87,87,87,87,88,88,88,89,89,88,88.
根据以上信息,下列结论正确的为( )
A、 B、 C、二班成绩的众数在乙组 D、一班成绩的中位数为87分9. 如图是标准跷跷板的示意图,横板 的中点过支撑点O,且绕点O只能上下转动.如果 , ,则小孩玩耍时,跷跷板可以转动的最大角度为( )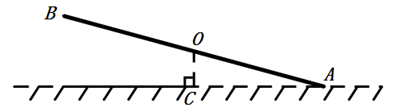 A、15° B、20° C、30° D、40°10.
A、15° B、20° C、30° D、40°10.如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2 , 四边形ABCD面积是11cm2 , 则①②③④四个平行四边形周长的总和为( )cm.
 A、45 B、46 C、47 D、4811. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )
A、45 B、46 C、47 D、4811. 如图,在等腰 与等腰 中, , , ,连接 和 相交于点 ,交 于点 ,交 与点 .则下列结论:① ;② ;③ 平分 ;④若 ,则 .一定正确的是( )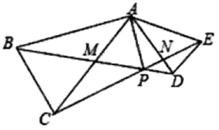 A、①②③ B、①②④ C、①③④ D、②③④12. 某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在点Pk(xk , yk)处,其中x1=1,y1=1,当k≥2时, ,[a]表示非负实数a的整数部分,例如[2.8]=2,[0.3]=0。按此方案,第2021棵树种植点的坐标为( )A、(1,405) B、(2,403) C、(2,405) D、(1,403)
A、①②③ B、①②④ C、①③④ D、②③④12. 某校数学课外小组,在坐标纸上为学校的一块空地设计植树方案如下:第k棵树种植在点Pk(xk , yk)处,其中x1=1,y1=1,当k≥2时, ,[a]表示非负实数a的整数部分,例如[2.8]=2,[0.3]=0。按此方案,第2021棵树种植点的坐标为( )A、(1,405) B、(2,403) C、(2,405) D、(1,403)二、填空题
-
13. 因式分解: .14. 小林和小华参加社会实践活动,随机选择“打扫社区卫生”“参加社会调查”其中一项.那么两人同时选择“参加社会调查”的概率是.15. 某垃圾处理厂日处理垃圾 吨,实施垃圾分类后,每小时垃圾的处理量比原来提高 ,这样日处理同样多的垃圾就少用 .若设实施垃圾分类前每小时垃圾的处理量为 吨,则可列方程.16. 如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了米。
 17. 如图,在矩形 中, , ,以点B为圆心, 的长为半径作 交 于点E;以点A为圆心, 的长为半径作 交 于点F,则图中阴影部分的面积为.
17. 如图,在矩形 中, , ,以点B为圆心, 的长为半径作 交 于点E;以点A为圆心, 的长为半径作 交 于点F,则图中阴影部分的面积为. 18.
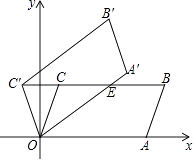
18.如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为 .
三、解答题
-
19. 计算(1)、计算:;(2)、先化简,再求值: ,其中 .20. 为了提高学生书写汉字的能力,增强保护汉字的意识,某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每符合题意听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别
成绩x分
频数(人数)
第1组
4
第2组
8
第3组
16
第4组
a
第5组
10

请结合图表完成下列各题:
(1)、求表中a的值;(2)、请把频数分布直方图补充完整;(3)、若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?(4)、第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.21. 如图,已知Rt△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F. (1)、求证:AE=AF;(2)、若AE=5,AC=4,求BE的长.22. 关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高 米,象征关公享年 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图, 代表底座的高,坡顶A与底座底部C处在同一水平面上,该游客在斜坡底P处测得该底座顶端B的仰角为 ,然后他沿着坡度为 的斜坡 攀行了 米,在坡顶A处又测得该底座顶端B的仰角为 .求:
(1)、求证:AE=AF;(2)、若AE=5,AC=4,求BE的长.22. 关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高 米,象征关公享年 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图, 代表底座的高,坡顶A与底座底部C处在同一水平面上,该游客在斜坡底P处测得该底座顶端B的仰角为 ,然后他沿着坡度为 的斜坡 攀行了 米,在坡顶A处又测得该底座顶端B的仰角为 .求: (1)、坡顶A到地面 的距离;(2)、求底座 的高度(结果精确到 米).
(1)、坡顶A到地面 的距离;(2)、求底座 的高度(结果精确到 米).(参考数据: ,
23. 为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,经过市场调查,购买一台 型设备比购买一台 型设备多花费2万元,购买2台A型设备比购买3台B型设备少花费6万元.(1)、购买一台A型设备、购买一台B型设备各需要多少万元;(2)、治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案.24. (1)、如图①,在正方形中,的顶点E,F分别在 , 边上,高与正方形的边长相等,求的度数.(2)、如图②,在中, , , 点M,N是边上的任意两点,且 , 将绕点A逆时针旋转至位置,连接 , 试判断 , , 之间的数量关系,并说明理由.(3)、在图①中,连接分别交 , 于点M,N,若 , , , 求 , 的长.25. 如图 ,抛物线 与 轴交于 、 两点,与 轴交于点 ,已知点 坐标为 ,点 坐标为 .
(1)、如图①,在正方形中,的顶点E,F分别在 , 边上,高与正方形的边长相等,求的度数.(2)、如图②,在中, , , 点M,N是边上的任意两点,且 , 将绕点A逆时针旋转至位置,连接 , 试判断 , , 之间的数量关系,并说明理由.(3)、在图①中,连接分别交 , 于点M,N,若 , , , 求 , 的长.25. 如图 ,抛物线 与 轴交于 、 两点,与 轴交于点 ,已知点 坐标为 ,点 坐标为 .

 (1)、求抛物线的表达式;(2)、如图 ,点 为直线 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标;(3)、如图 ,过点 作直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、如图 ,点 为直线 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标;(3)、如图 ,过点 作直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.