山东省济南市槐荫区2022年九年级数学线上测试试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. -5的绝对值的相反数是( )A、-5 B、0 C、1 D、52. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图所示,该几何体的主视图为( )
3. 如图所示,该几何体的主视图为( )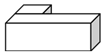 A、
A、 B、
B、 C、
C、 D、
D、 4. 在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途径城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示为( )A、13×103 B、1.3×103 C、13×104 D、1.3×1045. 下列运算正确的是( )A、 B、 C、 D、6. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
4. 在国家“一带一路”战略下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途径城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示为( )A、13×103 B、1.3×103 C、13×104 D、1.3×1045. 下列运算正确的是( )A、 B、 C、 D、6. 为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: = =13, = =15:s甲2=s丁2=3.6,s乙2=s丙2=6.3.则麦苗又高又整齐的是( )
A、甲 B、乙 C、丙 D、丁7. 化简的结果是( ).A、 B、 C、 D、8. 如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=( ) A、20° B、30° C、40° D、50°9. 如图,直线l是函数的图象.若点P(a,b)满足 , 且 , 则P点的坐标可能是( )
A、20° B、30° C、40° D、50°9. 如图,直线l是函数的图象.若点P(a,b)满足 , 且 , 则P点的坐标可能是( ) A、 B、 C、 D、10. 如图为某城市部分街道示意图,四边形为正方形,点G在对角线上, , , , 小敏行走的路线为 , 小聪行走的路线为 . 若小敏行走的路程为 , 则小聪行走的路程为( )m.
A、 B、 C、 D、10. 如图为某城市部分街道示意图,四边形为正方形,点G在对角线上, , , , 小敏行走的路线为 , 小聪行走的路线为 . 若小敏行走的路程为 , 则小聪行走的路程为( )m.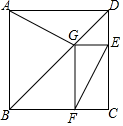 A、3600 B、4100 C、4600 D、610011. 小明去爬山,在山脚A看山顶D的仰角 , 小明在坡比为的山坡上走1300米到达B处,此时小明看山顶的仰角 , 则山高为( )米
A、3600 B、4100 C、4600 D、610011. 小明去爬山,在山脚A看山顶D的仰角 , 小明在坡比为的山坡上走1300米到达B处,此时小明看山顶的仰角 , 则山高为( )米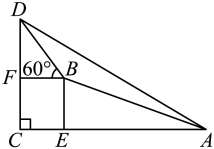 A、 B、 C、 D、12. 如图,在矩形中, , E是的中点,于点F,则的长是( )
A、 B、 C、 D、12. 如图,在矩形中, , E是的中点,于点F,则的长是( ) A、1 B、1.2 C、 D、2
A、1 B、1.2 C、 D、2二、填空题
-
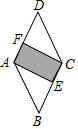
13. 分解因式: .14. 如果正多边形的一个外角为 , 那么它的边数是 .15. 如图,将菱形纸片ABCD固定后进行投针训练.已知纸片上AE⊥BC于E,CF⊥AD于F,sinD= . 如果随意投出一针命中菱形纸片,则命中矩形区域的概率是 .
 16. 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如果中, , 那么顶角A的正对记作 , 这时= . 容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,填空:如果的正弦函数值为 , 那么的值为 .17. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.
16. 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对().如果中, , 那么顶角A的正对记作 , 这时= . 容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,填空:如果的正弦函数值为 , 那么的值为 .17. 如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加m.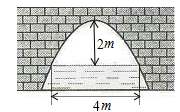 18. 如图,直线与y轴交于点A,与直线交于点B,以AB为边向右作菱形ABCD,点C恰好与原点O重合.抛物线的顶点在直线上移动.若抛物线与菱形的边都有公共点,则h的取值范围是 .
18. 如图,直线与y轴交于点A,与直线交于点B,以AB为边向右作菱形ABCD,点C恰好与原点O重合.抛物线的顶点在直线上移动.若抛物线与菱形的边都有公共点,则h的取值范围是 .
三、解答题
-
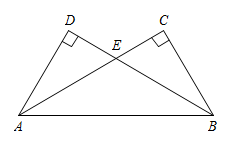
19. 先化简,再求值: , 其中 .20. 关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根.(1)、求m的取值范围;(2)、写出一个满足条件的m的值,并求此时方程的根.21. 如图,已知于点C,于点D,交于点E.求证: .
 22. 某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:
22. 某校以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查数据绘制了如下不完整的统计表和扇形统计图:运动项目
频数
频率
篮球
36
羽毛球
m
乒乓球
24
n
跳绳
12
其他
18

请根据以图表信息解答下列问题:
(1)、统计表中的m= , n= ;(2)、在扇形统计图中,“篮球”所在扇形的圆心角为度;(3)、该学校共2400名学生,据此估计有多少名学生最喜爱乒乓球?(4)、将2名最喜爱篮球的学生和2名最喜爱羽毛球的学生编为一组,从中随机抽取两人,请用列表或画树状图的方法求出所抽取的两人都选择了最喜爱篮球的概率.23. 如图,为的直径,A、C是圆上的两点,且 , 交于点E,已知 , (1)、求的长;(2)、过点A作的切线 , 交的延长线于点F,求的长.24. 为了节约水资源,某地区对居民用水实行阶梯水价制度,将居民全年用水量(取整数)划分为三档,标准如下
(1)、求的长;(2)、过点A作的切线 , 交的延长线于点F,求的长.24. 为了节约水资源,某地区对居民用水实行阶梯水价制度,将居民全年用水量(取整数)划分为三档,标准如下阶梯
居民家庭全年用水量
(立方米)
水价
(元/立方米)
其中
水费
(元/立方米)
水资源费
(元/立方米)
污水处理费
(元/立方米)
第一阶梯
0-180(含)
5
2.07
1.57
1.36
第二阶梯
181-260(含)
7
4.07
第三阶梯
260以上
9
6.07
如该地某户全年用水量为250立方米.则其应缴全年综合水费(含水费、水资源费、污水处理费)合计为(元)
(1)、如该地某户全年用水量为300立方米.则其应缴全年综合水费(含水费、水资源费、污水处理费)合计为多少元?(2)、如该地某户缴纳全年综合水费(含水费、水资源费、污水处理费)1180元,求该户全年用水量是多少立方米?25. 如图,等边和等边的一边都在x轴上,双曲线经过的中点C和的中点D.已知等边的边长为4. (1)、求k的值;(2)、求等边的边长;(3)、将等边绕点A任意旋转,得到等边 , P是的中点(如图2所示),连结 , 直接写出的最大值.26.(1)、【探究发现】
(1)、求k的值;(2)、求等边的边长;(3)、将等边绕点A任意旋转,得到等边 , P是的中点(如图2所示),连结 , 直接写出的最大值.26.(1)、【探究发现】
如图1,∠EOF的顶点O在正方形ABCD两条对角线的交点处,∠EOF=90°,将∠EOF绕点O旋转,旋转过程中,∠EOF的两边分别与正方形ABCD的边BC和CD交于点E和点F(点F与点C,D不重合).则CE,CF,BC之间满足的数量关系是 .
(2)、【类比应用】如图2,若将(1)中的“正方形ABCD”改为“∠BCD=120°的菱形ABCD”,其他条件不变,当∠EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.
(3)、【拓展延伸】如图3,∠BOD=120°,OD= , OB=4,OA平分∠BOD,AB= , 且OB>2OA,点C是OB上一点,∠CAD=60°,求OC的长.
27. 如图,直线与x轴交于点 , 与y轴交于点B,抛物线经过点A,B.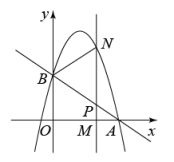
 (1)、求点B的坐标和抛物线的解析式;(2)、M为线段上一动点,过点M且垂直于x轴的直线与直线及抛物线分别交于点P,N.若以B,P,N为顶点的三角形与相似,求点M的坐标;(3)、将抛物线在之间的部分记为图象L,将图象L在直线上方部分沿直线翻折,其余部分保持不动,得到一个新的函数图象,记这个函数的最大值为a,最小值为b,若 , 请直接写出t的取值范围.
(1)、求点B的坐标和抛物线的解析式;(2)、M为线段上一动点,过点M且垂直于x轴的直线与直线及抛物线分别交于点P,N.若以B,P,N为顶点的三角形与相似,求点M的坐标;(3)、将抛物线在之间的部分记为图象L,将图象L在直线上方部分沿直线翻折,其余部分保持不动,得到一个新的函数图象,记这个函数的最大值为a,最小值为b,若 , 请直接写出t的取值范围.