山东省济南东南片区2022年中考一模数学试题

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{1}{2}$ 的相反数是（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 如图是由6个相同的正方体堆成的物体，它的左视图是（　　）

A、 B、 C、 D、

查看试题解析
3. 2021年5月15日07时18分，我国首个火星探测器“天问一号”经过470000000公里旅程成功着陆在火星上，从此，火星上留下中国的脚印，同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为（）

A、 $47 \times 10^{7}$ B、 $4.7 \times 10^{7}$ C、 $4.7 \times 10^{8}$ D、 $0.47 \times 10^{9}$

查看试题解析
4. 如图，直线 $D E // B F ， R t △ A B C$ 的顶点 $B$ 在 $B F$ 上，若 $∠ C B F = 20 °$ ，则 $∠ A D E =$ （）

A、 $70 °$ B、 $60 °$ C、 $75 °$ D、 $80 °$

查看试题解析
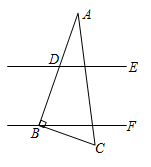5. 垃圾分类功在当代利在千秋，下列垃圾分类指引标志图形中，是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 实数a，b在数轴上的位置如图所示，则下列式子正确的是（）

A、 $a > b$ B、 $a + b > 0$ C、 $a b > 0$ D、 $| a | > | b |$

查看试题解析
7. 化简 $\frac{x^{2}}{x - 2} + \frac{4}{2 - x}$ 的结果是（）

A、 $x + 2$ B、 $x - 2$ C、 $\frac{1}{x - 2}$ D、 $\frac{2}{x + 2}$

查看试题解析
8. 小颖有两顶帽子，分别为红色和黑色，有三条围巾，分别为红色、黑色和白色，她随机拿出一顶帽子和一条围巾戴上，恰好为红色帽子和红色围巾的概率是（）

A、 $\frac{5}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{6}$

查看试题解析
9. 在同一平面直角坐标系中，函数 $y = k x - k$ 与 $y = \frac{k}{x}$ 的大致图象可能是（　　）

A、 B、 C、 D、

查看试题解析
10. 如图， $△ A B C$ 中， $A B ＝ A C = 3 \sqrt{5}$ ， $B C = 6$ ，分别以点B、C为圆心，大于 $\frac{1}{2} B C$ 的长为半径作弧，两弧交于点E，作射线 $A E$ ，在射线 $A E$ 上任取一点D，连接 $D C$ ．若 $C D = 5$ ，则 $A D$ 的长为（　　）

A、10 B、11 C、12 D、6 $\sqrt{5}$

查看试题解析
11. 如图，为了测量某建筑物 $B C$ 的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，沿斜坡 $A D$ 行走100米至坡顶D处，再从D处沿水平方向继续前行若干米到点E处，在E点测得该建筑物顶端C的仰角为59°，建筑物底端B的俯角为 $45 °$ ，点A、B、C、D、E在同一平面内，斜坡 $A D$ 的坡度 $i = 1 ： \frac{4}{3}$ .根据以上数据，计算出建筑物BC的高度约为（结果精确到1.参考数据： $s i n 59 ° \approx 0.86$ ， $c o s 59 ° \approx 0.52$ ， $t a n 59 ° \approx 1.66$ ）（）

A、158米 B、161米 C、159米 D、160米

查看试题解析
12. 在抛物线 $y ＝ a x^{2} - 4 a x + 2 (a > 0)$ ）上，若对于 $t < x_{1} < t + 1$ ， $t + 2 < x_{2} < t + 3$ ，都有 $y_{1} \neq y_{2}$ ，则t的取值范围是（　　）

A、 $t \geq 1$ B、 $t \geq 1$ 或 $t \leq 0$ C、 $t \leq 0$ D、 $t \geq 1$ 或 $t \leq - 1$

查看试题解析

二、填空题

13. 分解因式：3ab－ac＝；

查看试题解析
14. 若一个正多边形的内角和等于外角和的两倍，则该正多边形的边数是 .

查看试题解析
15. 一个不透明的袋子里装有3个红球和5个黑球，它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为.

查看试题解析
16. 如图，等边 $Δ A B C$ 中， $A B = 6$ ，点O为 $A B$ 的中点，以O为圆心，以 $O B$ 为半径作半圆，交 $A C ， B C$ 于点E，F，则图中阴影部分的面积是．

查看试题解析
17. 已知A，B两地相距120km，甲、乙两人沿同一条公路从A地出发到B地，甲骑摩托车，乙骑自行车．图中 $D E$ ， $O C$ 分别表示甲，乙离开A地的路程s（km）与时间t（h）的函数关系，则乙出发小时被甲追上．

查看试题解析
18. 如图，在正方形 $A B C D$ 中， $A B = 4$ ，点E为 $C D$ 上一动点， $A E$ 交 $B D$ 于点F，过点F作 $F H ⊥ A E$ ，交 $B C$ 于H，连接 $A H$ 交 $B D$ 于点P，过H作 $H G ⊥ B D$ 于点G，下列结论：① $A F = F H$ ， ② $△ C E H$ 的周长是7，③ $B D = 2 F G$ ， ④ $△ A F P ∽ △ A H E$ ．其中正确的是（写正确结论的序号）．

查看试题解析

三、解答题

19. 计算： ${(- 4)}^{0} - \sqrt{12} + 4 s i n 60 ° - (- 2)$ ．

查看试题解析
20. 解不等式组： ${\begin{array}{l} x + 4 > 3 x \\ x \leq \frac{x + 1}{2} \end{array}$ ，并写出它的所有非负整数解．

查看试题解析
21. 如图，菱形 $A B C D$ 中， $C E ⊥ A B$ 交 $A B$ 于点E， $C F ⊥ A D$ 交 $A D$ 于点F．
求证： $A E = A F$ ．

查看试题解析

22. 为了让全校学生牢固树立爱国爱党的崇高信念，某校举行了一次党史知识竞赛（百分制）.现从初一、初二两个年级各随机抽取了15名学生的测试成绩，得分用x表示，共分成4组：A：

60 \leq x < 70

， B：

70 \leq x < 80

， C：

80 \leq x < 90

， D：

90 \leq x \leq 100

，对成绩进行整理分析，得到了下面部分信息：

初一的测试成绩在C组中的数据为：81，85，88．

初二的测试成绩为：76，83，71，100，81，100，82，88，95，90，100，86，89，93，86．

年级	平均数	中位数	最高分	众数
初一	88	a	98	98
初二	88	88	100	b

(1)、a＝， b＝；

(2)、请补全条形统计图；

(3)、若初一有400名学生，请估计此次测试成绩初一达到90分及以上的学生有多少人？

查看试题解析

23. 如图，已知 $△ A B C$ 的边 $A B$ 是⊙O的切线，切点为E， $A C$ 经过圆心O并与圆相交于点F， $C B$ 交 $⊙ O$ 于D，连接 $C E ， D E ， E F$ ，且 $D E = E F$ ．

(1)、求证： $A B ⊥ B C$ ；

(2)、若 $B C = 3 ， s i n A = \frac{3}{5}$ ，求 $A F$ 的长．

查看试题解析
24. 某汽车贸易公司销售A、B两种型号的新能源汽车，A型车进货价格为每台12万元，B型车进货价格为每台15万元，该公司销售2台A型车和5台B型车，可获利3.1万元，销售1台A型车和2台B型车，可获利1.3万元.

(1)、求销售一台A型、一台B型新能源汽车的利润各是多少万元？

(2)、该公司准备用不超过300万元资金，采购A、B两种新能源汽车共22台，问最少需要采购A型新能源汽车多少台？

查看试题解析
25. 图，在平面直角坐标系中，矩形 $O A B C$ 的顶点B的坐标为 $(4 ， 2)$ ， $O A$ ， $O C$ 分别落在x轴和y轴上， $O B$ 是矩形的对角线，将 $△ O A B$ 绕点O逆时针旋转，使点B落在y轴上，得到 $△ O D E$ ， $O D$ 与 $C B$ 相交于点F，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点F，交 $A B$ 于点G．

(1)、求 $t a n ∠ C O F$ 的值及反比例函数表达式．

(2)、在x轴上是否存在一点M，使 $| M F - M G |$ 的值最大？若存在，求出点M；若不存在，说明理由．

(3)、在线段 $O A$ 上存在这样的点P，使得 $△ P F G$ 是等腰三角形，请直接写出 $O P$ 的长．

查看试题解析
26. 在△ABC中，∠ACB＝90°，AC＝BC，点D是直线AB上的一动点（不与点A，B重合），连接CD，在CD的右侧以CD为斜边作等腰直角三角形CDE，点H是BD的中点，连接EH．

(1)、如图1，当点D是AB的中点时，线段EH与AD的数量关系是， EH与AD的位置关系是；

(2)、如图2，当点D在边AB上且不是AB的中点时，（1）中的结论是否仍然成立？若成立，请仅就图2中的情况给出证明；若不成立，请说明理由；

(3)、若AC＝BC＝2 $\sqrt{2}$ ，其他条件不变，连接AE，BE．当△BCE是等边三角形时，请直接写出△ADE的面积．

查看试题解析
27. 如图，抛物线 $y = a x^{2} + b x + 2$ 与x轴交于点A，B，与y轴交于点C，已知A，B两点坐标分别是 $A (1 ， 0)$ ， $B (- 4 ， 0)$ ，连接 $A C ， B C$ ．

(1)、求抛物线的表达式；

(2)、将 $Δ A B C$ 沿 $B C$ 所在直线折叠，得到 $Δ D B C$ ，点A的对应点D是否落在抛物线的对称轴上？若点D在对称轴上，请求出点D的坐标；若点D不在对称轴上，请说明理由；

(3)、若点P是抛物线位于第二象限图象上的一动点，连接 $A P$ 交 $B C$ 于点Q，连接BP， $Δ B P Q$ 的面积记为 $S_{1}$ ， $Δ A B Q$ 的面积记为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值最大时点P的坐标．

查看试题解析