山东省济南东南片区2022年中考二模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 实数 , 3,0,中,最大的数是( )A、 B、3 C、0 D、2. 下列立体图形中,其俯视图与主视图完全相同的是( )A、
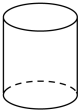 B、
B、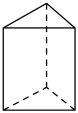 C、
C、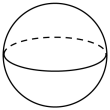 D、
D、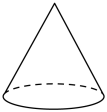 3. 2022年2月4日晚,第二十四届冬季奥林匹克运动会开幕式在北京国家体育场举行.约有19000人参与冬奥志愿服务,将数字19000用科学记数法表示为( )A、 B、 C、 D、4. 如图,CD∥AB,直线l分别与直线相交于点E、F,平分交直线于点G,若 , 则的度数为( )
3. 2022年2月4日晚,第二十四届冬季奥林匹克运动会开幕式在北京国家体育场举行.约有19000人参与冬奥志愿服务,将数字19000用科学记数法表示为( )A、 B、 C、 D、4. 如图,CD∥AB,直线l分别与直线相交于点E、F,平分交直线于点G,若 , 则的度数为( ) A、 B、 C、 D、5. 2022年新年贺词中提到“人不负青山,青山定不负人”,下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )A、
A、 B、 C、 D、5. 2022年新年贺词中提到“人不负青山,青山定不负人”,下列四个有关环保的图形中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,的顶点都在方格线的格点上,将绕点A逆时针方向旋转 , 得到 , 则点C的对应点的坐标为( )
6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,的顶点都在方格线的格点上,将绕点A逆时针方向旋转 , 得到 , 则点C的对应点的坐标为( ) A、 B、 C、 D、8. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( )
A、 B、 C、 D、8. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( ) A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月9. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、10. 如图,在中, , , , 依据尺规作图的痕迹,则的面积为( )
A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月9. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、10. 如图,在中, , , , 依据尺规作图的痕迹,则的面积为( ) A、12 B、 C、 D、11. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A、12 B、 C、 D、11. 某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)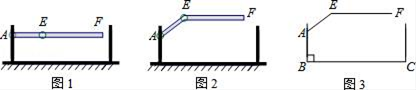 A、
A、 B、
B、 C、
C、 D、
D、 12. 已知抛物线与x轴交于两点,当时,y随x的增大而增大,则下列结论中:①;②;③;④若图象上两点对一切正数n,总有 , 则 , 则正确的个数为( )A、1 B、2 C、3 D、4
12. 已知抛物线与x轴交于两点,当时,y随x的增大而增大,则下列结论中:①;②;③;④若图象上两点对一切正数n,总有 , 则 , 则正确的个数为( )A、1 B、2 C、3 D、4二、填空题
-
13. 因式分解: .14. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的吉祥码示意图,用黑白打印机打印在边长为2cm的正方形区域内,图中黑色部分的总面积为2.4cm2 , 现在向正方形区域内随机掷点,点落入黑色部分的概率为 .
 15. 若代数式 和 的值相等,则x= .16. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 .
15. 若代数式 和 的值相等,则x= .16. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 . 17. 如图,已知A、B两地相距4千米,甲从A地出发步行到B地,20分钟后乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为 .
17. 如图,已知A、B两地相距4千米,甲从A地出发步行到B地,20分钟后乙从B地出发骑自行车到A地,甲乙两人离A地的距离(千米)与甲所用时间(分)之间的关系如图所示,由图中的信息可知,乙到达A地的时间为 . 18. 如图,在矩形中, , E在边上且 . 若点H在边上,将矩形沿直线折叠,折叠后点D落在上的点处,过点作于点N,与交于点M,则的值为 .
18. 如图,在矩形中, , E在边上且 . 若点H在边上,将矩形沿直线折叠,折叠后点D落在上的点处,过点作于点N,与交于点M,则的值为 .
三、解答题
-
19. 计算:20. 解不等式组 , 并写出它的所有整数解.21. 如图,▱ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.
 22. 为庆祝中国共产党建党100周年,某校开展了以“百年党史今天读”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成A,B,C,D,E五个等级,并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
22. 为庆祝中国共产党建党100周年,某校开展了以“百年党史今天读”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成A,B,C,D,E五个等级,并绘制了如下不完整的统计图.请结合统计图,解答下列问题: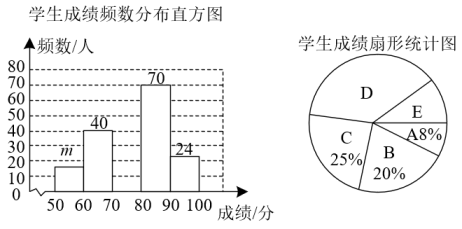
等级
成绩x
A
B
C
D
E
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中m=;(2)、补全学生成绩频数分布直方图;(3)、扇形统计图中D等级对应的圆心角为度;(4)、若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少人?23. 如图,在中, , 点O在斜边上,以O为圆心,为半径作圆,分别与相交于点D,E,连接 . 已知是的切线. (1)、求证:;(2)、若 , 求的半径.24. 书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.(1)、求毛笔和宣纸的单价;(2)、计划用不多于360元的资金购买毛笔,宣纸的数量共计200,则学校最多可以购买多少支毛笔?25. 如图,一次函数与反比例函数的图象交于点和 , 与y轴交于点C.
(1)、求证:;(2)、若 , 求的半径.24. 书法是中华民族的文化瑰宝,是人类文明的宝贵财富,是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸,已知购买40支毛笔和100张宣纸需要280元;购买30支毛笔和200张宣纸需要260元.(1)、求毛笔和宣纸的单价;(2)、计划用不多于360元的资金购买毛笔,宣纸的数量共计200,则学校最多可以购买多少支毛笔?25. 如图,一次函数与反比例函数的图象交于点和 , 与y轴交于点C. (1)、求一次函数与反比例函数的表达式;(2)、过点A作轴于点D,点P是反比例函数在第一象限的图象上一点,设直线与线段交于点E,当时,求点P的坐标;(3)、在(2)的条件下,点M是上的一个动点,当是以为斜边的直角三角形时,求点M的坐标.26.(1)、【方法尝试】
(1)、求一次函数与反比例函数的表达式;(2)、过点A作轴于点D,点P是反比例函数在第一象限的图象上一点,设直线与线段交于点E,当时,求点P的坐标;(3)、在(2)的条件下,点M是上的一个动点,当是以为斜边的直角三角形时,求点M的坐标.26.(1)、【方法尝试】如图1,矩形是矩形以点A为旋转中心,按逆时针方向旋转所得的图形,分别是它们的对角线.则与数量关系 , 位置关系;
 (2)、【类比迁移】
(2)、【类比迁移】如图2,在和中, . 将绕点A在平面内逆时针旋转,设旋转角为α(),连接 . 请判断线段和的数量关系和位置关系,并说明理由;
 (3)、【拓展延伸】
(3)、【拓展延伸】如图3,在中, , 过点A作 , 在射线上取一点D,连接 , 使得 , 请求线段的最大值.
 27. 已知,如图,在平面直角坐标系中,A(-3,0)、B(1,0),把点A绕原点逆时针旋转,使其落在y轴负半轴点C处,抛物线y=ax2+bx+c过A、B、C三点,连接AC.
27. 已知,如图,在平面直角坐标系中,A(-3,0)、B(1,0),把点A绕原点逆时针旋转,使其落在y轴负半轴点C处,抛物线y=ax2+bx+c过A、B、C三点,连接AC. (1)、求抛物线的解析式;(2)、把直线AC向上平移、平移后的直线DM交y轴于点D,交y轴右侧的抛物线于点M,连接AM、CM、若 , 求点M的坐标;(3)、点N为直线BC上一个动点,设点N的横坐标为n,若以A、C、N三点组成的三角形为钝角三角形、试求出n的取值范围.
(1)、求抛物线的解析式;(2)、把直线AC向上平移、平移后的直线DM交y轴于点D,交y轴右侧的抛物线于点M,连接AM、CM、若 , 求点M的坐标;(3)、点N为直线BC上一个动点,设点N的横坐标为n,若以A、C、N三点组成的三角形为钝角三角形、试求出n的取值范围.