山东省菏泽市牡丹区2022年九年级中考三模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,用正、负数来表示只有相反意义的量.一次数学测试,以80分为基准简记,90分记作+10分,那么70分应记作( )A、+10分 B、0分 C、-10分 D、-20分2. 图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
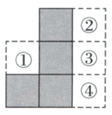 A、区域①处 B、区域②处 C、区域③处 D、区域④处3. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( )
A、区域①处 B、区域②处 C、区域③处 D、区域④处3. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是( ) A、
A、 B、
B、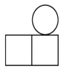 C、
C、 D、
D、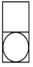 4. 一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )
4. 一副三角板摆放如图所示,斜边FD与直角边AC相交于点E,点D在直角边BC上,且FDAB,∠B=30°,则∠ADB的度数是( )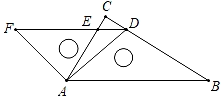 A、95° B、105° C、115° D、125°5. 为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如下表:
A、95° B、105° C、115° D、125°5. 为了传承传统手工技艺,提高同学们的手工制作能力,某中学七年级一班的美术老师特地给学生们开了一节手工课,教同学们编织“中国结”,为了了解同学们的学习情况,便随机抽取了20名学生,对他们的编织数量进行统计,统计结果如下表:编织数量/个
2
3
4
5
6
人数/人
3
6
5
4
2
请根据上表,判断下列说法正确的是( )
A、样本为20名学生 B、众数是4个 C、中位数是3个 D、平均数是3.8个6. 能说明命题“关于x的方程一定有实根”是假命题的反例为( )A、 B、 C、 D、7. 当温度不变时,气球内气体的气压P(单位:)是气体体积V(单位:)的函数,下表记录了一组实验数据:V(单位:)
1
1.5
2
2.5
3
P(单位:)
96
64
48
38.4
32
P与V的函数关系可能是( )
A、 B、 C、 D、8. 如图,在中, , 正方形的边长为2,且边在线段上,点F,B,C在同一条直线上,将正方形沿射线方向平移,当点F与点C重合时停止运动,设点F平移的距离为x,平移过程中两图重叠部分的面积为y,则下列函数图象中能大致反映y与x之间的函数关系的是( )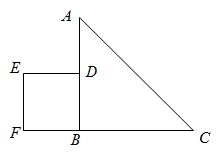 A、
A、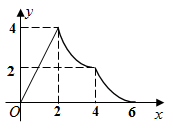 B、
B、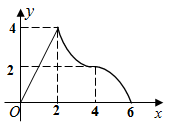 C、
C、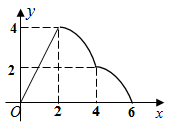 D、
D、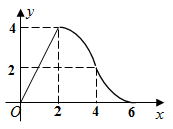
二、填空题
-
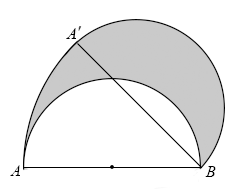
9. 对于我们而言,水是生命之源,但对于在轨驻留的航天员而言,水和氧气都是生命之源.在过去的1年里,3名神舟十三号航天员顺利完成长达6个月的在轨驻留,创造了新的纪录.中国空间站有一套非常完善的“再生生保”系统,解决了生活用水和氧气问题.我们来简单地算一笔账,一个成年人一天需要570升氧气,那么3名航天员每天需要约1700升氧气,6个月需要约31万升氧气,则31万这个数用科学记数法表示为 .10. 关于x的不等式组的解是 , 那么a的取值范围是 .11. 已知方程的两根为2和-2,分解因式 .12. 如图,AB为半径的直径,且AB=6,半圆绕点B顺时针旋转45°,点A旋转到的位置,则图中阴影部分的面积为 .
 13. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,若点A(2,2),B(3,4),C(6,1),B'(6,8),则△A'B'C'的面积为 .
13. 如图,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,若点A(2,2),B(3,4),C(6,1),B'(6,8),则△A'B'C'的面积为 .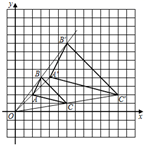 14. 数轴上 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处.按照这样的规律继续跳动到点 ( , 是整数)处,那么线段 的长度为( , 是整数).
14. 数轴上 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处.按照这样的规律继续跳动到点 ( , 是整数)处,那么线段 的长度为( , 是整数).
三、解答题
-
15. 计算: .16. 先化简 , 再求值,其中x,y是方程组的解.17. 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D,
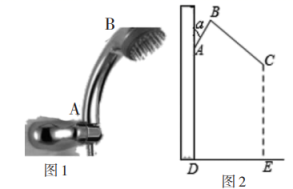
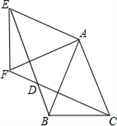 (1)、求证:BE=CF ;(2)、当四边形ACDE为菱形时,求BD的长.18. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长与墙壁的夹角 ,喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使.问:安装师傅应将支架固定在离地面多高的位置?
(1)、求证:BE=CF ;(2)、当四边形ACDE为菱形时,求BD的长.18. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点处,手柄长与墙壁的夹角 ,喷出的水流与形成的夹角 , 现在住户要求:当人站在处淋浴时,水流正好喷洒在人体的处,且使.问:安装师傅应将支架固定在离地面多高的位置?(结果精确到 , 参考数据:)
 19. 疫情防控,人人有责.某公司为了解决员工的口罩问题上,准备采购A、B两种型号的口罩,A种口罩每件单价比B种口罩每件多200元,用3000元购进A种口罩和用1800元购进B种口罩的数量相同.(1)、A种口罩每件的单价和B种口罩的单价各是多少元?(2)、公司计划用15000元的资金购进A、B两种型号的口罩共40件,其中A种口罩数量不得低于B种口罩数量的一半,该公司的几种采购方案?20. 如图,在平面直角坐标系中,函数的图象G经过点 , 直线与x轴交于点B.
19. 疫情防控,人人有责.某公司为了解决员工的口罩问题上,准备采购A、B两种型号的口罩,A种口罩每件单价比B种口罩每件多200元,用3000元购进A种口罩和用1800元购进B种口罩的数量相同.(1)、A种口罩每件的单价和B种口罩的单价各是多少元?(2)、公司计划用15000元的资金购进A、B两种型号的口罩共40件,其中A种口罩数量不得低于B种口罩数量的一半,该公司的几种采购方案?20. 如图,在平面直角坐标系中,函数的图象G经过点 , 直线与x轴交于点B.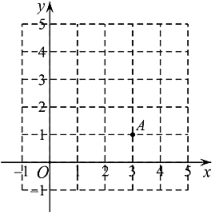 (1)、求m的值及点B的坐标;(2)、直线与函数的图象G交于点C,记图象G在点A,C之间的部分与线段 , , 围成的区域(不含边界)为W.
(1)、求m的值及点B的坐标;(2)、直线与函数的图象G交于点C,记图象G在点A,C之间的部分与线段 , , 围成的区域(不含边界)为W.①当时,直接写出区域W内的整点个数;
②若区域W内恰有2个整点,结合函数图象,求k的取值范围.
21. 丰富的网络资源改变了人们的学习方式,某校为了解学生每周末利用网络资源进行自主学习的情况.在本校随机抽取80名学生进行问卷调查,现将调查结果绘制成不完整的统计图表,请根据图表中的信息解答下列问题:组别
学习时间x(h)
频数(人数)
A
8
B
24
C
32
D
n
E
4小时以上
4
(1)、表中的n= , 中位数落在组;(2)、请补全频数分布直方图;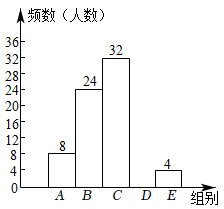 (3)、B组对应扇形圆心角的度数为 .
(3)、B组对应扇形圆心角的度数为 .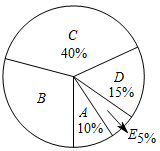 (4)、该校准备召开学习经验分享会,计划在E组学生中随机选出两人作经验交流,已知E组的四名学生中,七、八年级各有1人,九年级有2人.请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.22. 如图,以的边AB为直径作 , 交BC于点D,点E是弧BD的中点,连接AE与BC交于点F, .
(4)、该校准备召开学习经验分享会,计划在E组学生中随机选出两人作经验交流,已知E组的四名学生中,七、八年级各有1人,九年级有2人.请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.22. 如图,以的边AB为直径作 , 交BC于点D,点E是弧BD的中点,连接AE与BC交于点F, . (1)、求证:AC是的切线:(2)、若 , , 求BF的长.23.
(1)、求证:AC是的切线:(2)、若 , , 求BF的长.23. (1)、问题
(1)、问题如图1,在四边形中,点P为上一点,当时,求证: .
(2)、探究若将角改为锐角(如图2),其他条件不变,上述结论还成立吗?说明理由.
(3)、应用如图3,在中, , , 以点A为直角顶点作等腰 . 点D在上,点E在上,点F在上,且 , 若 , 求的长.
24. 如图,直线与x轴交于点C,与y轴交于点B,抛物线经过B,C两点.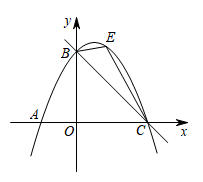 (1)、求抛物线的解析式;(2)、E是直线BC上方抛物线上的一动点,当点E到直线BC的距离最大时,求点E的坐标;(3)、Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形?若存在,请求出点P的坐标:若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、E是直线BC上方抛物线上的一动点,当点E到直线BC的距离最大时,求点E的坐标;(3)、Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P,Q,B,C为顶点的四边形是平行四边形?若存在,请求出点P的坐标:若不存在,请说明理由.