山东省菏泽市巨野县2022年中考数学二模试卷

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果温度上升2℃记作+2℃，那么温度下降3℃记作（）

A、 $+ 2$ ℃ B、 $- 2$ ℃ C、 $+ 3$ ℃ D、 $- 3$ ℃

查看试题解析
2. 下列运算正确的是（）．

A、 $a^{2} \times a^{3} = a^{5}$ B、 ${(a^{2})}^{3} = a^{5}$ C、 ${(a b)}^{3} = a b^{3}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
3. 如图， $A B ∥ C D$ ， $∠ F G B ＝ 154 °$ ， $F G$ 平分 $∠ E F D$ ，则 $∠ A E F$ 的度数等于（）．

A、26° B、52° C、54° D、77°

查看试题解析
4. 下列图形中，既是轴对称图形又是中心对称图形的是（　　　）

A、 B、 C、 D、

查看试题解析
5. 扬帆中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 $x m$ ，则可列方程为（）

A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$ C、 $30 x + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$

查看试题解析
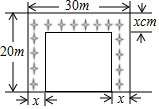6. 小强同学从 $- 1$ ， $0$ ， $1$ ， $2$ ， $3$ ， $4$ 这六个数中任选一个数，满足不等式 $x + 1 < 2$ 的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
7. 如图，在▱ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接CE，若△CED的周长为6，则▱ABCD的周长为（）

A、6 B、12 C、18 D、24

查看试题解析
8. 如图，已知矩形 $A B C D$ 中，点E是 $B C$ 边上的点 $A E = B C ， D F ⊥ A E$ ， $B E = 2 ， E C = 1$ ，垂足为F下列结论：① $△ A D F ≌ △ E A B$ ；② $A F = E B$ ；③ $D F$ 平分 $∠ A D C$ ；④ $s i n ∠ C D F = \frac{2}{3} .$ 其中正确的结论有（　　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 北京故宫的占地面积约为720000m² ，将720000用科学记数法表示为．

查看试题解析
10. 因式分解：a³+2a²+a= ．

查看试题解析
11. 甲，乙两人进行飞镖比赛，每人各投6次.甲的成绩(单位:环)为:9，8，9.6，10，6.甲、乙两人平均成绩相等，乙成绩的方差为4.那么成绩较为稳定的是.(填“甲”或“乙“).

查看试题解析
12. 如图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A= ．

查看试题解析
13. 若分式方程 $\frac{3 x - a}{x^{2} - 2 x}$ ＋ $\frac{1}{x - 2}$ ＝ $\frac{2}{x}$ 有增根，则实数a的取值是．

查看试题解析
14. 如图，在矩形纸片ABCD中，AB＝2，AD＝3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．

查看试题解析

三、解答题

15. 计算： $- 2 c o s 30 ° + | 1 - \sqrt{3} | + \frac{\sqrt{32}}{\sqrt{8}}$ ．

查看试题解析
16. 解不等式组： ${\begin{array}{l} 4 x - 7 < 5 (x + 1) \\ \frac{x}{3} < 3 - \frac{x - 2}{2} \end{array}$

查看试题解析
17. 如图，在▱ABCD中，点E是BC上的一点，连接DE ，在DE上取一点F使得∠AFE＝∠ADC ．若DE＝AD ，求证：DF＝CE ．

查看试题解析
18. 如图1，我国古建筑的大门上常常悬挂着巨大的匾额，图2中的线段 $B C$ 就是悬挂在墙壁AM上的某块匾额的截面示意图.已知 $B C = 2$ 米， $∠ M B C = 37 °$ .从水平地面点D处看点C，仰角 $∠ A D C = 45 °$ ，从点 $E$ 处看点 $B$ ，仰角 $∠ A E B = 53 °$ .且 $D E = 4.4$ 米，求匾额悬挂的高度 $A B$ 的长.（参考数据： $\sin 37 ° \approx \frac{3}{5}$ ， $\cos 37 ° \approx \frac{4}{5}$ ， $\tan 37 ° \approx \frac{3}{4}$ ）

查看试题解析
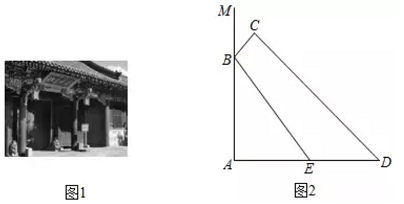19. 央视“经典咏流传”开播以来受到社会广泛关注，我市也在各个学校开展了传承经典的相关主题活动“戏曲进校园”，某校对此项活动的喜爱情况进行了随机调查，对收集的信息进行统计，绘制了下面两副尚不完整的统计图，请你根据统计图所提供的信息解答下列问题：图中A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”．

(1)、被调查的总人数是人，扇形统计图中B部分所对应的扇形圆心角的度数为，并补全条形统计图；

(2)、若该校共有学生1800人，请根据上述调查结果估计该校学生中A类有多少人；

(3)、在A类5人中，刚好有3个女生2个男生，从中随机抽取两个同学担任两角色，用树状图或列表法求出被抽到的两个学生性别相同的概率．

查看试题解析
20. 如图，反比例函数 $y = \frac{k}{x}$ 上的图象与一次函数 $y = m x + n$ 的图象相交于 $A (a ， - 1)$ ， $B (- 1 ， 3)$ 两点.

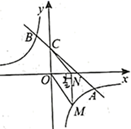(1)、求反比例函数和一次函数的解析式；

(2)、设直线 $A B$ 交y轴于点C，点 $N (t ， 0)$ 是正半轴上的一个动点，过点N作 $N M ⊥ x$ 轴交反比例函数 $y = \frac{k}{x}$ 的图象于点M，连接 $C N$ ， $O M$ .若 $S_{四边形 C O M N} > 3$ ，求t的取值范围.

查看试题解析
21. 为进一步落实“德、智、体、美、劳”五育并举工作，某中学以体育为突破口，准备从体育用品商场一次性购买若干个足球和篮球，用于学校球类比赛活动.每个足球的价格都相同，每个篮球的价格也相同.已知篮球的单价比足球单价的2倍少30元，用1200元购买足球的数量是用900元购买篮球数量的2倍.

(1)、足球和篮球的单价各是多少元？

(2)、根据学校实际情况，需一次性购买足球和篮球共200个，但要求足球和篮球的总费用不超过15500元，学校最多可以购买多少个篮球？

查看试题解析
22. 如图，AB是⊙O的直径，OC是半径，延长OC至点D.连接AD，AC，BC.使∠CAD＝∠B.

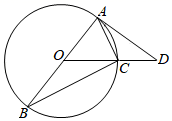(1)、求证：AD是⊙O的切线；

(2)、若AD＝4，tan∠CAD＝ $\frac{1}{2}$ ，求BC的长.

查看试题解析
23. 在数学兴趣小组活动中，小亮进行数学探究活动．

(1)、 $△ A B C$ 是边长为3的等边三角形，E是边 $A C$ 上的一点，且 $A E = 1$ ，小亮以 $B E$ 为边作等边三角形 $B E F$ ，如图①，求 $C F$ 的长；

(2)、 $△ A B C$ 是边长为3的等边三角形，E是边 $A C$ 上的一个动点，小亮以 $B E$ 为边作等边三角形 $B E F$ ，如图②，在点E从点C到点A的运动过程中，求点F所经过的路径长；

(3)、 $△ A B C$ 是边长为3的等边三角形，M是高 $C D$ 上的一个动点，小亮以 $B M$ 为边作等边三角形 $B M N$ ，如图③，在点M从点C到点D的运动过程中，求点N所经过的路径长．

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + 6$ 经过 $A (- 2 ， 0)$ 、 $B (4 ， 0)$ 两点，与y轴交于点C，D是抛物线上一动点，设点D的横坐标为 $m (1 < m < 4)$ ，连结 $A C ， B C ， D B ， D C$ ．

(1)、求抛物线的函数表达式．

(2)、当 $△ B C D$ 的面积等于 $△ A O C$ 的面积的 $\frac{3}{4}$ 时，求m的值．

(3)、当 $m = 2$ 时，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B、D、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的的坐标；若不存在，请说明理由．

查看试题解析