山东省菏泽市单县2022年中考三模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 实数a,b在数轴上的位置如图所示,则下列式子正确的是( )
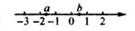 A、|a|>|b| B、a>b C、ab>0 D、a+b>02. 一列数4,5,6,4,4,7,x,5的平均数是5,则中位数和众数分别是( )A、4,4 B、5,4 C、5,6 D、6,73. 下列运算正确的是( )A、 B、 C、 D、4. 已知二元一次方程组 , 则的值为( )A、2 B、6 C、 D、5. 已知 , ,则 的值是( )A、2 B、 C、3 D、6. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( )
A、|a|>|b| B、a>b C、ab>0 D、a+b>02. 一列数4,5,6,4,4,7,x,5的平均数是5,则中位数和众数分别是( )A、4,4 B、5,4 C、5,6 D、6,73. 下列运算正确的是( )A、 B、 C、 D、4. 已知二元一次方程组 , 则的值为( )A、2 B、6 C、 D、5. 已知 , ,则 的值是( )A、2 B、 C、3 D、6. 如图,在 中, , , ,将 绕点A逆时针旋转得到 ,使点 落在AB边上,连结 ,则 的值为( ) A、 B、 C、 D、7. 如图, 是 的外接圆, 交 于点E,垂足为点D, , 的延长线交于点F.若 , ,则 的长是( )
A、 B、 C、 D、7. 如图, 是 的外接圆, 交 于点E,垂足为点D, , 的延长线交于点F.若 , ,则 的长是( )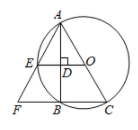 A、10 B、8 C、6 D、48. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:
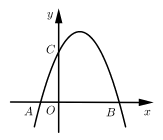
A、10 B、8 C、6 D、48. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:① ;②当 时,y随x的增大而增大;③ ;④ .
其中正确的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
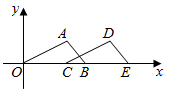
9. 若一个扇形的圆心角为 ,面积为 ,则这个扇形的弧长为 (结果保留 )10. 已知x=1是一元二次方程(m-2)x2+4x-m2=0的一个根,则m的值是 .11. 关于x的不等式组 恰好有2个整数解,则实数a的取值范围是.12. 如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为.
 13. 如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为 .
13. 如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为 . 14. 如图,在平面直角坐标系中,将边长为1的正方形绕点O顺时针旋转45°后得到正方形 , 依此方式,绕点O连续旋转2019次得到正方形 , 那么点的坐标是 .
14. 如图,在平面直角坐标系中,将边长为1的正方形绕点O顺时针旋转45°后得到正方形 , 依此方式,绕点O连续旋转2019次得到正方形 , 那么点的坐标是 .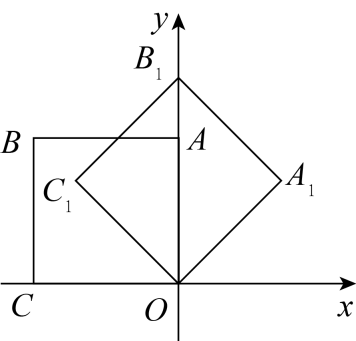
三、解答题
-
15. 计算: .16. 先化简,再求值: , 其中a,b满足 .17. 如图,在 和 中, , .
 (1)、求证: ;(2)、若 , ,求 的长.18. 由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 在北偏东 方向上,航行 海里到达 点,这时测得小岛 在北偏东 方向上,小岛 周围 海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由.
(1)、求证: ;(2)、若 , ,求 的长.18. 由我国完全自主设计,自主建造的首艘国产航母于2018年5月成功完成首次海上试验任务.如图,航母由西向东航行,到达 处时,测得小岛 在北偏东 方向上,航行 海里到达 点,这时测得小岛 在北偏东 方向上,小岛 周围 海里内有暗礁,如果航母不改变航线继续向东航行,有没有触礁危险?请说明理由. 19. 如图,已知反比例函数 的图象和一次函数 的图象都过点 ,过点P作y轴的垂线,垂足为A , O为坐标原点, 的面积为1.
19. 如图,已知反比例函数 的图象和一次函数 的图象都过点 ,过点P作y轴的垂线,垂足为A , O为坐标原点, 的面积为1.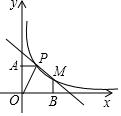 (1)、求反比例函数和一次函数的解析式;(2)、设反比例函数图象与一次函数图象的另一交点为M , 过M作x轴的垂线,垂足为B , 求五边形 的面积.20. 某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?21. 我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.
(1)、求反比例函数和一次函数的解析式;(2)、设反比例函数图象与一次函数图象的另一交点为M , 过M作x轴的垂线,垂足为B , 求五边形 的面积.20. 某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?21. 我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.用过的餐巾纸投放情况统计图

根据图中信息,解答下列问题:
(1)、此次调查一共随机采访了名学生,在扇形统计图中,“灰”所在扇形的圆心角的度数为度;(2)、补全条形统计图(要求在条形图上方注明人数);(3)、若该校有3600名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;(4)、李老师计划从A,B,C,D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛,请用树状图法或列表法求出恰好抽中A,B两人的概率.22. 如图,已知 是 的直径,C为 上一点, 的角平分线交 于点D,F在直线 上,且 ,垂足为E,连接 、 . (1)、求证: 是 的切线;(2)、若 , 的半径为3,求 的长.23. 如图1,在等腰Rt中, , 点D、E分别在边、上, , 连接,点M、P、N分别为、、的中点.
(1)、求证: 是 的切线;(2)、若 , 的半径为3,求 的长.23. 如图1,在等腰Rt中, , 点D、E分别在边、上, , 连接,点M、P、N分别为、、的中点.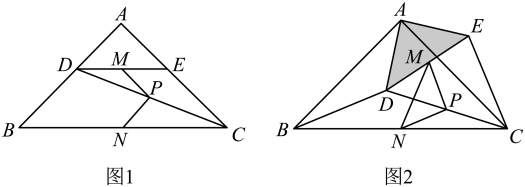 (1)、观察猜想:图1中,线段与的数量关系是 , 位置关系是;(2)、探究证明:把绕点A逆时针方向旋转到图2的位置,连接 , , 判断的形状,并说明理由;(3)、拓展延伸:把绕点A在平面内自由旋转,若 , , 求面积的最大值.24. 综合与探究
(1)、观察猜想:图1中,线段与的数量关系是 , 位置关系是;(2)、探究证明:把绕点A逆时针方向旋转到图2的位置,连接 , , 判断的形状,并说明理由;(3)、拓展延伸:把绕点A在平面内自由旋转,若 , , 求面积的最大值.24. 综合与探究如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.
 (1)、求抛物线的解析式;(2)、点D在抛物线的对称轴上,当△ACD的周长最小时,点D的坐标为 .(3)、点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;(4)、若点M是y轴上的动点,在坐标平面内是否存在点N,使以点A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点D在抛物线的对称轴上,当△ACD的周长最小时,点D的坐标为 .(3)、点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;(4)、若点M是y轴上的动点,在坐标平面内是否存在点N,使以点A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.