山东省东营市东营区2022年中考三模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
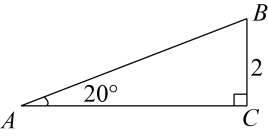
1. 2022相反数的倒数是( )A、 B、2021 C、-2021 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点.已知坡角为20°,山高千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
 A、 B、 C、 D、4. 如图,直线 ,将一个含 角的三角尺按如图所示的位置放置,若 ,则 的度数为( )
A、 B、 C、 D、4. 如图,直线 ,将一个含 角的三角尺按如图所示的位置放置,若 ,则 的度数为( ) A、 B、 C、 D、5. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )
A、 B、 C、 D、5. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、6. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )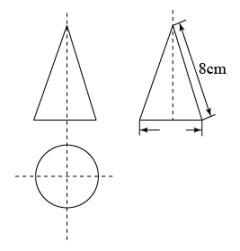 A、 B、 C、 D、7. 二次函数 的图象如图所示,下列说法中,错误的是( )
A、 B、 C、 D、7. 二次函数 的图象如图所示,下列说法中,错误的是( )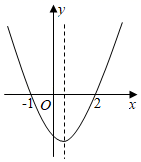 A、对称轴是直线 B、当 时, C、 D、8. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中, , .点P从点A出发,以2cm/s的速度在矩形的边上沿 运动,当点P与点D重合时停止运动.设运动的时间为 (单位:s), 的面积为S(单位: ),则S随t变化的函数图象大致为( )
A、对称轴是直线 B、当 时, C、 D、8. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、9. 如图,在矩形ABCD中, , .点P从点A出发,以2cm/s的速度在矩形的边上沿 运动,当点P与点D重合时停止运动.设运动的时间为 (单位:s), 的面积为S(单位: ),则S随t变化的函数图象大致为( )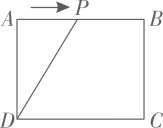 A、
A、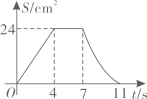 B、
B、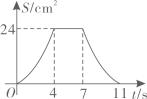 C、
C、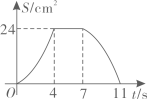 D、
D、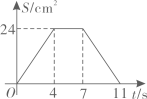 10. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
10. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )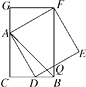 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
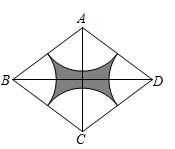
11. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用。经测算,一粒芝麻的质量约为0.00000201千克,将0.00000201用科学记数法表示为 .12. 因式分解: .13. “最美鄂州,从我做起”.“五四”青年节当天,马桥村青年志愿小组到胡林社区参加美化社区活动.6名志愿者参加劳动的时间(单位:小时)分别为:3,2,2,3,1,2,这组数据的中位数是.14. 如果关于x的一元二次方程有实数根,那么k应满足的条件是 .15. 如图,在菱形ABCD中,对角线 , ,分别以点A,B,C,D为圆心, 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为.(结果保留 )
 16. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.
16. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.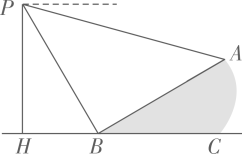 17. 在△ABC中,BA=BC,AC=14,S△ABC=84,D为AB上一动点,连接CD,过A作AE⊥CD于点E,连接BE,则BE的最小值是 .
17. 在△ABC中,BA=BC,AC=14,S△ABC=84,D为AB上一动点,连接CD,过A作AE⊥CD于点E,连接BE,则BE的最小值是 .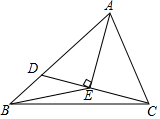 18. 如图, , 点是平分线上一点, , 作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;…按这样的方法继续下去,则的面积为(用含正整数n的代数式表示).
18. 如图, , 点是平分线上一点, , 作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;作 , , 垂足分别为点 , , 以为边作等边三角形;…按这样的方法继续下去,则的面积为(用含正整数n的代数式表示).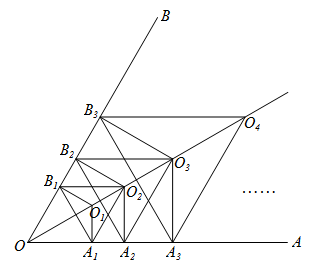
三、解答题
-
19.(1)、计算: .(2)、先化简,再求值: , 其中m满足: .20. 新学期,某校开设了“防疫宣传”“心理疏导”等课程.为了解学生对新开设课程的掌握情况,从九年级学生中随机抽取了部分学生进行了一次综合测试.测试结果分为四个等级:A级为优秀,B级为良好,C级为及格,D级为不及格.将测试结果绘制了如图两幅不完整的统计图.根据统计图中的信息解答下列问题:
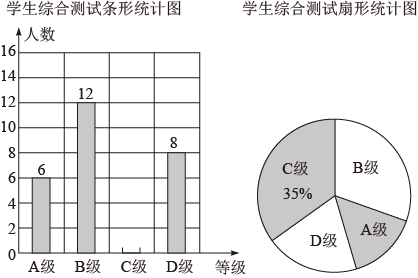 (1)、求扇形统计图中表示A级的扇形圆心角的度数,并把条形统计图补充完整;(2)、该校九年级共有学生860名,如果全部参加这次测试,估计“优秀”的人数;(3)、某班有4名优秀的同学(分别记为E、F、G、H,其中E为小明),班主任要从中随机选择两名同学进行经验分享.利用列表法或画树状图法,求小明被选中的概率.21. 以的一条边AC为直径的⊙O与BC相交于点D,点D是BC的中点,过点D作⊙O的切线交AB于点E.
(1)、求扇形统计图中表示A级的扇形圆心角的度数,并把条形统计图补充完整;(2)、该校九年级共有学生860名,如果全部参加这次测试,估计“优秀”的人数;(3)、某班有4名优秀的同学(分别记为E、F、G、H,其中E为小明),班主任要从中随机选择两名同学进行经验分享.利用列表法或画树状图法,求小明被选中的概率.21. 以的一条边AC为直径的⊙O与BC相交于点D,点D是BC的中点,过点D作⊙O的切线交AB于点E. (1)、求证:AB=AC;(2)、若BE=1, , 求⊙O的半径.22. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知 .
(1)、求证:AB=AC;(2)、若BE=1, , 求⊙O的半径.22. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知 .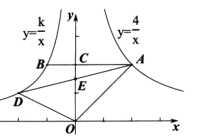 (1)、求直线的解析式;(2)、求反比例函数的解析式;(3)、点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.23. 某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.(1)、求每部A型手机和B型手机的销售利润分别为多少元?(2)、该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
(1)、求直线的解析式;(2)、求反比例函数的解析式;(3)、点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.23. 某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.(1)、求每部A型手机和B型手机的销售利润分别为多少元?(2)、该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.①求y关于n的函数关系式并写出n的取值范围;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
24. 如图直角坐标系中,O为坐标原点,抛物线y=﹣x2+6x+3交y轴于点A,过A作AB∥x轴,交抛物线于点B,连结OB.点P为抛物线上AB上方的一个点,连结PA,作PQ⊥AB垂足为H,交OB于点Q.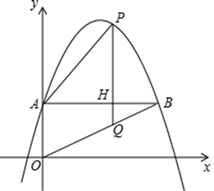 (1)、求AB的长;(2)、当∠APQ=∠B时,求点P的坐标;(3)、当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.25. 已知:如图①,在矩形ABCD中,AB=8,AD=6,连接AC,将三角形ABC沿AC翻折,使B点落在E点处,连接EC,AE,AE交DC于F点.
(1)、求AB的长;(2)、当∠APQ=∠B时,求点P的坐标;(3)、当△APH面积是四边形AOQH面积的2倍时,求点P的坐标.25. 已知:如图①,在矩形ABCD中,AB=8,AD=6,连接AC,将三角形ABC沿AC翻折,使B点落在E点处,连接EC,AE,AE交DC于F点.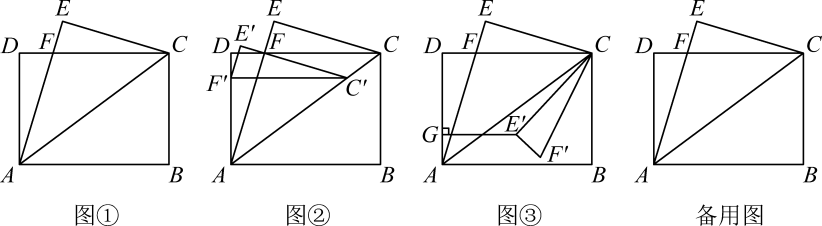 (1)、求DF的长.(2)、若将△CEF沿着射线CA方向平移,设平移的距离为m(平移距离指点C沿CA方向所经过的线段长度).当点F平移到线段AD上时,如图②,求出相应的m的值.(3)、如图③,将△CEF绕点C逆时针旋转一个角a(0°<a<∠ECB),记旋转中的△CEF为△CE′F′,过E′作E′G⊥AD于G点,在旋转过程中,当△DCE′为等腰三角形时,求出线段E′G的长度.
(1)、求DF的长.(2)、若将△CEF沿着射线CA方向平移,设平移的距离为m(平移距离指点C沿CA方向所经过的线段长度).当点F平移到线段AD上时,如图②,求出相应的m的值.(3)、如图③,将△CEF绕点C逆时针旋转一个角a(0°<a<∠ECB),记旋转中的△CEF为△CE′F′,过E′作E′G⊥AD于G点,在旋转过程中,当△DCE′为等腰三角形时,求出线段E′G的长度.