山东省德州市禹城市2022年中考一模数学试题

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. |﹣2|的倒数的相反数是（　　）

A、﹣2 B、﹣ $\frac{1}{2}$ C、2 D、 $\frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、 ${(a - b)}^{2} = a^{2} - b^{2}$ B、 ${(a^{3})}^{2} = a^{5}$ C、 $a^{5} \div a^{3} = a^{2}$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
3. 如图，直线a和直线b平行，∠1＝75°，∠2＝35°，则∠3的度数是（）

A、55° B、75° C、40° D、30°

查看试题解析
4.
如图所示几何体的左视图是（　　）

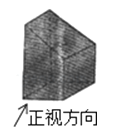A、 B、 C、 D、

查看试题解析
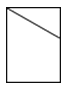5. 2020年6月23日，中国第55颗北斗导航卫星成功发射，顺利完成全球组网．其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片，已实现规模化应用，22纳米=0.000000022米，将0.000000022用科学记数法表示为（）

A、22×10⁸ B、2.2×10^-8 C、0.22×10^-7 D、22×10^-9

查看试题解析
6. 若点 $P (a + 2 ， 1 - a)$ 在第二象限，则a的取值范围是（）

A、 $- 2 < a < 1$ B、 $a < 1$ C、 $a > - 2$ D、 $a < - 2$

查看试题解析
7. 某企业车间有50名工人，某一天他们生产的机器零件个数统计如表：表中表示零件个数的数据中，众数、中位数分别是（　　）
零件个数（个）
6
7
8
人数（人）
15
22
13

A、7个，7个 B、7个，6个 C、22个，22个 D、8个，6个

查看试题解析
8. 下列命题正确的是（　　）

A、对角线互相垂直平分的四边形是菱形 B、长度相等的弧是等弧 C、与圆的半径垂直的直线是圆的切线 D、对角线相等的四边形是矩形

查看试题解析
9. 在△ABC中，∠ACB＝90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是（　　）

A、 B、 C、 D、

查看试题解析
10. 若关于x的方程 $x^{2} + 2 m x + m^{2} + 3 m - 2 = 0$ 有两个实数根x₁、x₂ ，则 $x_{1} (x_{2} + x_{1}) + x_{2}^{2}$ 的最小值为（）

A、-2 B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{4}$

查看试题解析
11. 在直径为10m的圆柱型油槽内注入一些油后，截面如图所示，液面宽AB＝6m，如果继续向油槽内注油，使液面宽为8m，那么液面上升了（）m

A、1 B、2 C、1或7 D、2或6

查看试题解析
12. 已知二次函数y＝ax²＋bx＋c的图象与x轴交于点（-2，0）、（x₁ ， 0），且1＜x₁＜2，与y轴的正半轴的交点在（0，2）的下方．下列结论：①a＜b＜0；②4a＋2b＋c＞0；③2a＋c＞0；④2a-b＋1＞0，其中符合题意结论的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 当 $x =$ 时，分式 $\frac{| x | - 3}{x - 3}$ 的值为0.

查看试题解析
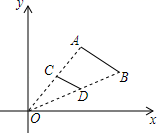
14. 若一个正多边形的外角和等于内角和的一半，则该正多边形的边数是．

查看试题解析
15. 如图，已知线段AB两个端点的坐标分别为A(4，6)，B(8，4)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的一半后得到线段CD ，则端点D坐标为．

查看试题解析
16. 如图，菱形ABCD的边长为2，∠ABC=60°，E是AD边的中点，点P是对角线BD上的动点，当AP+PE的值最小时，PD的长是．

查看试题解析
17. 如图，小文准备测量自己所住楼房与对面楼房的水平距离，他在对面楼房处放置一个3米长的标杆CD，然后他在A处测得C点的俯角β为53°．再测得D点的俯角α为45°，则两座楼房之间的水平距离大约为米．（参考数据： $s i n 53 ° \approx \frac{4}{5}$ ， $c o s 53 ° \approx \frac{3}{5}$ ， $t a n 53 ° \approx \frac{4}{3}$ ）

查看试题解析
18. 在直角坐标系中，等腰直角三角形 $A_{1} B_{1} O$ 、 $A_{2} B_{2} B_{1}$ 、 $A_{3} B_{3} B_{2}$ 、…、 $A_{n} B_{n} B_{n - 1}$ 按如图所示的方式放置，其中点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ 、…、 $A_{n}$ 均在一次函数 $y = k x + b$ 的图象上，点 $B_{1}$ 、 $B_{2}$ 、 $B_{3}$ 、…、 $B_{n}$ 均在x轴上．若点 $B_{1}$ 的坐标为 $(1 ， 0)$ ，点 $B_{2}$ 的坐标为 $(3 ， 0)$ ，则点 $A_{2022}$ 的坐标为．

查看试题解析

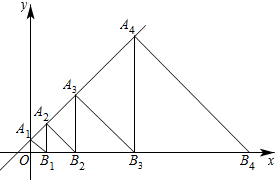
三、解答题

19. 先化简，再求值： $(\frac{x^{2} + x - 2}{x + 1} - 2) \div \frac{x - 2}{x + 1}$ ，其中x为 $x^{2} + 3 x - 10 = 0$ 的解．

查看试题解析
20. 某校七年级举办了“古诗词背诵比赛”活动，并进行了评比：A为优秀；B为良好；C为合格；D为不合格．九（1）班的语文老师对本班学生的成绩做了统计，绘制了下列两幅尚不完整的统计图，请根据下列所给信息回答问题：

(1)、该班共有人，扇形统计图中的D所对应的圆心角为度．

(2)、请根据以上信息补全条形统计图．

(3)、老师准备从D类学生中随机抽取2人再次背诵．已知D类学生中有3名男生，1名女生，求恰好选中1名男生和1名女生的概率．

查看试题解析
21. 请同学们结合探究一次函数，反比例函数，二次函数图象和性质的过程，继续探究函数 $y = \frac{6}{x + 1}$ 的图像和性质．
第一步：列表；
x
……
-7
-5
a
-3
-2
0
1
2
3
5
……
$y = \frac{6}{x + 1}$
……
-1
-1.5
-2
-3
-6
6
3
2
b
1
……
第二步：描点；
第三步：连线．

(1)、计算表中a和b的值：a： b：，并将该函数在直线 $x = - 1$ 左侧部分的图像描点画出；

(2)、试着描述函数 $y = \frac{6}{x + 1}$ 的性质：
①x的取值范围：；
②y的取值范围：；
③图像的增减性：；
④图像的对称性：；

(3)、已知一次函数 $y = k x + b$ 与 $y = \frac{6}{x + 1}$ 相交于点C（1，3），D（-5，-1.5），结合图像直接写出关于x的不等式 $k x + b > \frac{6}{x + 1}$ 的解集．

查看试题解析
22. 园林部门计划在某公园建一个长方形苗圃ABCD．苗圃的一面靠墙（墙最大可用长度为14米）．另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留1米宽的门（门不用木栏），建成后所用木栏总长22米，设苗圃ABCD的一边CD长为x米．

(1)、苗圃ABCD的另一边BC长为米（用含x的代数式表示）；

(2)、若苗圃ABCD的面积为45m，求x的值；

(3)、当x为何值时，苗圃ABCD的面积最大，最大面积为多少平方米？

查看试题解析
23. 如图，AB是⊙O的直径，C是⨀O上一点，E为OD延长线上一点，D是 $\overset{⌢}{A C}$ 的中点且∠CAE＝∠AOE．AC与OE交于点F．

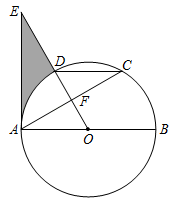(1)、请说明：AE是⨀O的切线；

(2)、若DC∥AB，DC＝1，求阴影部分面积．

查看试题解析
24. 如图， $△ A B C$ 与 $△ A C D$ 为正三角形，点O为射线 $C A$ 上的动点，将射线 $O M$ 绕点O逆时针旋转 $60 °$ ，得到射线 $O N$

(1)、如图1，点O与点A重合时，点E，F分别在线段 $B C$ ， $C D$ 上，求证： $△ A E C ≌ △ O F D$ ；

(2)、如图2，当点O在 $C A$ 的延长线上时，E，F分别在线段 $B C$ 的延长线和线段 $C D$ 的延长线上，请写出 $C E$ 、 $C F$ 、 $C O$ 三条线段之间的数量关系，并说明理由；

查看试题解析
25. 如图，抛物线y $= - \frac{3}{8}$ x²+bx+c过A（4，0），B（2，3）两点，交y轴于点C．动点P从点C出发，以每秒5个单位长度的速度沿射线CA运动，设运动的时间为t秒．

(1)、求抛物线y $= - \frac{3}{8}$ x²+bx+c的表达式；

(2)、过点P作PQ $∥$ y轴，交抛物线于点Q．当t $= \frac{1}{4}$ 时，求PQ的长；

(3)、若在平面内存在一点M，使得以A，B，P，M为顶点的四边形是菱形，求点M的坐标．

查看试题解析

x	……	-7	-5	a	-3	-2	0	1	2	3	5	……
$y = \frac{6}{x + 1}$	……	-1	-1.5	-2	-3	-6	6	3	2	b	1	……

零件个数（个）	6	7	8
人数（人）	15	22	13