山东省德州市武城县2022年中考二模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 下列实数中,最大的数是( )A、 B、 C、 D、32. 如图,几何体的左视图是( )
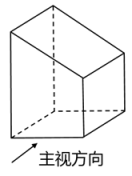 A、
A、
B、
B、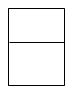
C、
C、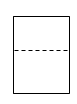
D、
D、
3. 截止到 2019 年 9 月 3 日,电影《哪吒之魔童降世》的累计票房达到 47.24 亿,47.24 亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )
3. 截止到 2019 年 9 月 3 日,电影《哪吒之魔童降世》的累计票房达到 47.24 亿,47.24 亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为( )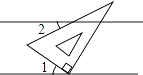 A、10° B、20° C、25° D、30°5. 三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( )
A、10° B、20° C、25° D、30°5. 三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,则B点转过的路径长为( ) A、 π B、 π C、2π D、3π6. 将正方形纸片按图①方式依次对折得图②的 ,点D是 边上一点,沿线段 剪开,展开后得到一个正八边形,则点D应满足( )
A、 π B、 π C、2π D、3π6. 将正方形纸片按图①方式依次对折得图②的 ,点D是 边上一点,沿线段 剪开,展开后得到一个正八边形,则点D应满足( ) A、 B、 C、 D、7. 下列说法错误的是( )A、平分弦的直径,垂直于弦,并且平分弦所对的弧 B、已知⊙O的半径为6,点O到直线a的距离为5,则直线a与⊙O有两个交点 C、如果一个三角形的外心在三角形的外部,则这个三角形是钝角三角形 D、三角形的内心到三角形的三边的距离相等8. 小华在整理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有同一性质是( )A、互相平分 B、相等 C、互相垂直 D、平分一组对角9. 九年级学生去距学校10 km的博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为x km/h,则所列方程正确的是( )A、 B、 C、 D、10. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )
A、 B、 C、 D、7. 下列说法错误的是( )A、平分弦的直径,垂直于弦,并且平分弦所对的弧 B、已知⊙O的半径为6,点O到直线a的距离为5,则直线a与⊙O有两个交点 C、如果一个三角形的外心在三角形的外部,则这个三角形是钝角三角形 D、三角形的内心到三角形的三边的距离相等8. 小华在整理平行四边形、矩形、菱形、正方形的性质时,发现它们的对角线都具有同一性质是( )A、互相平分 B、相等 C、互相垂直 D、平分一组对角9. 九年级学生去距学校10 km的博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为x km/h,则所列方程正确的是( )A、 B、 C、 D、10. 图①是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图②所示的四边形 . 若 , , 则的值为( )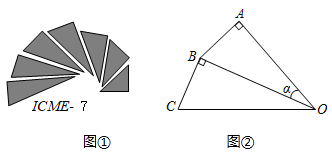 A、 B、 C、 D、11. 关于x的方程kx2+(2k-1)x+k-3=0有实数根,则k的取值范围是( )A、k≥- B、k≥-且k≠0 C、k>- D、k>-且k≠012. 二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )
A、 B、 C、 D、11. 关于x的方程kx2+(2k-1)x+k-3=0有实数根,则k的取值范围是( )A、k≥- B、k≥-且k≠0 C、k>- D、k>-且k≠012. 二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如表所示,则下列结论中,正确的个数有( )x
﹣1
0
1
3
y
﹣1
3
5
3
①a<0;②当x<0时,y<3;③当x>1时,y的值随x值的增大而减小;④方程ax2+bx+c=5有两个不相等的实数根.
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 分解因式的结果是 .14. 已知a,b是方程x2+x-3=0的两个实数根,则a2+b2+2015的值是 .15. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.16. 在半径为2的⊙O中,弦AB为2,则弦AB所对的圆周角的度数为 .17. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为 .
 18. 如图,直线l:y= x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此做法进行下去,点A4的坐标为;点An的坐标为 .
18. 如图,直线l:y= x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1 , 以原点O 为圆心,OB1长为半径画弧交y一轴于点A2;再过点A2作y轴的垂线交直线于点B2 , 以原点O为圆心,OB2长为半径画弧交y轴于点A3 , …,按此做法进行下去,点A4的坐标为;点An的坐标为 .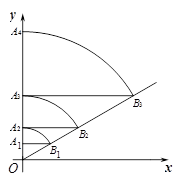
三、解答题
-
19. 先化简,再求值: ,其中20.
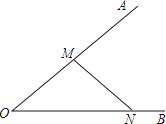
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
 21. 自我省深化课程改革以来,铁岭市某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
21. 自我省深化课程改革以来,铁岭市某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.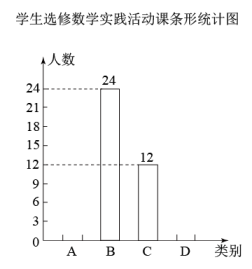

根据图中信息解决下列问题:
(1)、本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;(2)、补全条形统计图;(3)、选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.22. 为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?(3)、在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?23. 如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD. (1)、求证:CE是⊙O的切线:(2)、连接BE,若⊙O的半径长为5,OF=3,求EF的长,24.(1)、方法探索:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.(根据所给的铺助线完成证明)
(1)、求证:CE是⊙O的切线:(2)、连接BE,若⊙O的半径长为5,OF=3,求EF的长,24.(1)、方法探索:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.(根据所给的铺助线完成证明)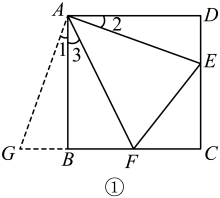 (2)、方法拓展:如图②.在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.
(2)、方法拓展:如图②.在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.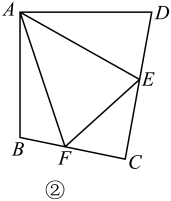 (3)、知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.
(3)、知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.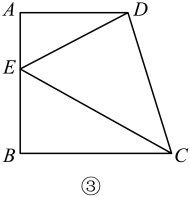 25. 如图,直线l: 与x轴、y轴分别交于点B、C,经过B、C两点的抛物线 与x轴的另一个交点为A.
25. 如图,直线l: 与x轴、y轴分别交于点B、C,经过B、C两点的抛物线 与x轴的另一个交点为A.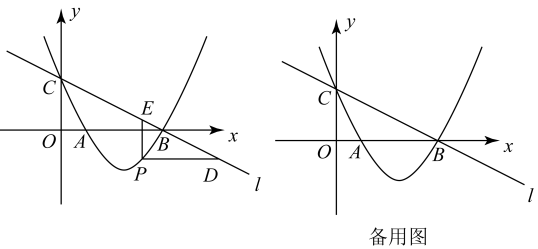 (1)、求该抛物线的解析式;(2)、若点P在直线l下方的抛物线上,过点P作轴交l于点D,轴交l于点E,求的最大值;(3)、设F为直线l上的点,点P仍在直线l下方的抛物线上,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
(1)、求该抛物线的解析式;(2)、若点P在直线l下方的抛物线上,过点P作轴交l于点D,轴交l于点E,求的最大值;(3)、设F为直线l上的点,点P仍在直线l下方的抛物线上,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.