山东省德州市临邑县2022年中考二模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 的相反数等于( )A、 B、4 C、 D、±2. 近年来,新冠肺炎给人类带来了巨大灾难,经科学家研究,冠状病毒多数为球形或近似球形,其直径约为0.00000011米,其中数据0.00000011用科学记数法表示正确的是( )A、 B、 C、 D、3. 把a3-4a分解因式正确的是( )A、a(a2-4) B、a(a-2)2 C、a(a+2)(a-2) D、a(a+4)(a-4).4. 一副三角板如图所示摆放,若 ,则 的度数是( )
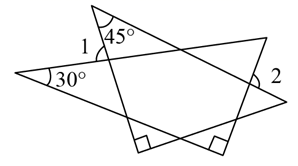 A、80° B、95° C、100° D、110°5. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,26. 将矩形沿折叠,得到如图所示的图形,已知 , 则的大小是( )
A、80° B、95° C、100° D、110°5. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,26. 将矩形沿折叠,得到如图所示的图形,已知 , 则的大小是( )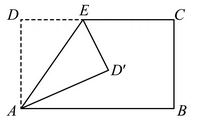 A、 B、 C、 D、7. 一个菱形被一条直线分成面积为x,y的两部分,则y与x之间的函数图象只可能是( )A、
A、 B、 C、 D、7. 一个菱形被一条直线分成面积为x,y的两部分,则y与x之间的函数图象只可能是( )A、 B、
B、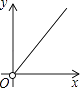 C、
C、 D、
D、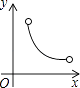 8. 如图, 是 的直径,点A,C在 上, , 交 于点G.若 .则 的度数为( )
8. 如图, 是 的直径,点A,C在 上, , 交 于点G.若 .则 的度数为( )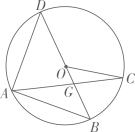 A、 B、 C、 D、9. 若二次函数中x与y的对应值如下表:
A、 B、 C、 D、9. 若二次函数中x与y的对应值如下表:x
0
y
6
3
2
3
则当时,y的值为( )
A、4 B、6 C、7 D、1210. 关于x的方程有两个实数根 , , 且 , 那么m的值为( )A、 B、 C、或1 D、或411. 关于二次函数的三个结论,①图象与y轴的交点为;②对任意实数m,都有与对应的函数值相等;③图象经过点;其中,正确结论是( )A、①② B、②③ C、①③ D、①②③12. 如图,在△ABC中,AD,BE分别是BC,AC边上的中线,且AD⊥BE,垂足为点F,设BC=a,AC=b,AB=c,则下列关系式中成立的是( ) A、a2+b2=5c2 B、a2+b2=4c2 C、a2+b2=3c2 D、a2+b2=2c2
A、a2+b2=5c2 B、a2+b2=4c2 C、a2+b2=3c2 D、a2+b2=2c2二、填空题
-
13. 正八边形的一个内角的度数是 度。
14. 计算: .15. 某校开展读书日活动,小亮和小莹分别从校图书馆的“科技”、“文学”两类书籍中随机地抽取一本,抽到同一类书籍的概率是 .16. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .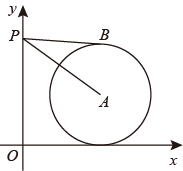 17. 如图,四边形为菱形, , 延长到E,在内作射线 , 使得 , 过点D作 , 垂足为F,若 , 则对角线的长为 .
17. 如图,四边形为菱形, , 延长到E,在内作射线 , 使得 , 过点D作 , 垂足为F,若 , 则对角线的长为 .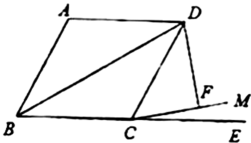 18. 人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的0.618法就应用了黄金分割数.设 , , 得 , 记 , , , …,则 .
18. 人们把这个数叫做黄金分割数,著名数学家华罗庚优选法中的0.618法就应用了黄金分割数.设 , , 得 , 记 , , , …,则 .三、解答题
-
19. 解不等式组: .20. 在甲、乙两名同学中选拔一人参加“中华好诗调”大赛,在相同的测试条件下,两人5次测试成绩(单位,分)如下:
甲:78,85,81,84,82
乙:88,79,90,81,72.
回答下列问题:
(1)、甲成绩的平均数是 , 乙成绩的平均数是;(2)、分别计算 , , 你认为选拔谁参加比赛更合适,说明理由;(3)、如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.21. 如图,在中,D是边上一点,且 . (1)、尺规作图(保留作图痕迹,不写作法);
(1)、尺规作图(保留作图痕迹,不写作法);①作的角平分线交于点E;
②作线段的垂直平分线交于点F.
(2)、的角平分线与线段的垂直平分线交于点O.连接、 , 请猜想和的数量关系并证明.22. 如图,在平面直角坐标系 中,一次函数 和 的图象相交于点 ,反比例函数 的图象经过点 .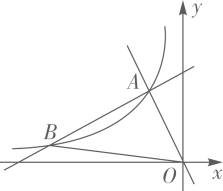 (1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.23. 如图1,在四边形 中, , , 是 的直径, 平分 .
(1)、求反比例函数的表达式;(2)、设一次函数 的图象与反比例函数 的图象的另一个交点为 ,连接 ,求 的面积.23. 如图1,在四边形 中, , , 是 的直径, 平分 .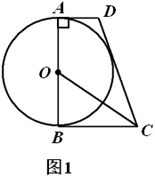 (1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
(1)、求证:直线 与 相切;(2)、如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.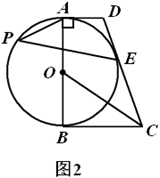 24. 将绕点A按逆时针方向旋转度,并使各边长变为原来的n倍,得 , 我们将这种变换记为 .
24. 将绕点A按逆时针方向旋转度,并使各边长变为原来的n倍,得 , 我们将这种变换记为 .

 (1)、如图①,对作变换得 , 则 , 直线与直线所夹的锐角为;(2)、如图②,中, , 对作变换得 , 的延长线交于点D,连接 , 若四边形为平行四边形,求和n的值;(3)、如图③,中, , 对作变换得 , 连接 , 试判断四边形的形状并说明理由.25. 如图,抛物线(其中a,m为正的常数)与x轴交于点A,B,与y轴交于点 , 顶点为F,CD//AB交抛物线于点D.
(1)、如图①,对作变换得 , 则 , 直线与直线所夹的锐角为;(2)、如图②,中, , 对作变换得 , 的延长线交于点D,连接 , 若四边形为平行四边形,求和n的值;(3)、如图③,中, , 对作变换得 , 连接 , 试判断四边形的形状并说明理由.25. 如图,抛物线(其中a,m为正的常数)与x轴交于点A,B,与y轴交于点 , 顶点为F,CD//AB交抛物线于点D. (1)、当时,求点D的坐标;(2)、在(1)的条件下若为抛物线(其中 . )上任意两点,直接写出当满足什么条件时, .(3)、若点E是第一象限抛物线上的点,满足 . 求点E的纵坐标.
(1)、当时,求点D的坐标;(2)、在(1)的条件下若为抛物线(其中 . )上任意两点,直接写出当满足什么条件时, .(3)、若点E是第一象限抛物线上的点,满足 . 求点E的纵坐标.