山东省德州地区2022年中考二模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 第24届冬季奥林匹克运动会于2022年2月4日至2月20日在中国北京市和张家口市联合举办,以下是参选的冬奥会会徽设计的部分图形,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在实数 , , 0,-1中,是无理数的是( )A、 B、0 C、 D、-13. 下列计算正确的是( )A、 B、 C、 D、4. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )
2. 在实数 , , 0,-1中,是无理数的是( )A、 B、0 C、 D、-13. 下列计算正确的是( )A、 B、 C、 D、4. 下图是由4个相同的正方体组成的立体图形,它的左视图是( )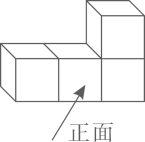 A、
A、 B、
B、 C、
C、 D、
D、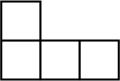 5. 某公司要招聘一名职员,根据实际需要,从学历、经验和能力三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表,
5. 某公司要招聘一名职员,根据实际需要,从学历、经验和能力三个方面对甲、乙、丙、丁四名应聘者进行了测试,测试成绩如表,项目
应聘者
甲
乙
丙
丁
学历
9
8
8
7
经验
8
6
9
5
能力
7
8
8
7
如果将学历、经验和能力三项得分按1∶1∶2的比例确定每人的最终得分,并以此为依据确定录用者,那么谁将被录用( )
A、甲 B、乙 C、丙 D、丁6. 在同一平面直角坐标系中,函数与的图象大致是( )A、 B、
B、 C、
C、 D、
D、 7. 已知不等式组 , 其解集在数轴上表示正确的是( )A、
7. 已知不等式组 , 其解集在数轴上表示正确的是( )A、 B、
B、 C、
C、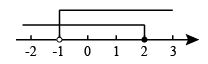 D、
D、 8. 如图,斗笠是一种遮挡阳光和蔽雨的编结帽,它可近似看成一个圆锥,已知该斗笠的侧面积为550πcm2 , AB是斗笠的母线,长为25cm,AO为斗笠的高,BC为斗笠末端各点所在圆的直径,则OC的值为( )
8. 如图,斗笠是一种遮挡阳光和蔽雨的编结帽,它可近似看成一个圆锥,已知该斗笠的侧面积为550πcm2 , AB是斗笠的母线,长为25cm,AO为斗笠的高,BC为斗笠末端各点所在圆的直径,则OC的值为( ) A、22 B、23 C、24 D、259. “行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段 横穿双向车道,其中, 米,在人行绿灯亮时,小刚共用时10秒通过 ,其中通过 的速度是通过 的1.3倍,求小刚通过 的速度.设小刚通过 的速度为x米/秒,则根据题意列方程为( )
A、22 B、23 C、24 D、259. “行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段 横穿双向车道,其中, 米,在人行绿灯亮时,小刚共用时10秒通过 ,其中通过 的速度是通过 的1.3倍,求小刚通过 的速度.设小刚通过 的速度为x米/秒,则根据题意列方程为( ) A、 B、 C、 D、10. 如图,从外一点A作的切线AB,切点为B,连接AO并延长交于点C,连接BC.若 , 则∠ACB的度数是( )
A、 B、 C、 D、10. 如图,从外一点A作的切线AB,切点为B,连接AO并延长交于点C,连接BC.若 , 则∠ACB的度数是( ) A、26° B、30° C、32° D、36°11. 已知A、B两地是一条直路,甲从A地到B地,乙从B地到A地,两人同时出发,乙先到达目的地,两人之间的距离与运动时间的函数关系大致如图所示,下列说法错误的是( )
A、26° B、30° C、32° D、36°11. 已知A、B两地是一条直路,甲从A地到B地,乙从B地到A地,两人同时出发,乙先到达目的地,两人之间的距离与运动时间的函数关系大致如图所示,下列说法错误的是( ) A、两人出发2h后相遇 B、甲骑自行车的速度为60km/h C、乙骑自行车的速度为90km/h D、乙比甲提前到达目的地12. 如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,前n行的点数和不能是以下哪个结果 ( )
A、两人出发2h后相遇 B、甲骑自行车的速度为60km/h C、乙骑自行车的速度为90km/h D、乙比甲提前到达目的地12. 如图,这是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点…,第n行有n个点…,前n行的点数和不能是以下哪个结果 ( ) A、741 B、600 C、465 D、300
A、741 B、600 C、465 D、300二、填空题
-
13. 若在实数范围内有意义,则实数x的取值范围是.14. 为防疫情,社区采取以一楼道为单位组织进行核酸检测.小明,小红所住楼道共30人,为加快检测进度,每10人一组,随机分成三组,小明和小红分到同一组检测的概率是 .15. 如图,多边形ABCDE为正五边形,则∠ACB的度数为 .
 16. 抛物线和x轴有公共点,则k的取值范围是 .17. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF,若BF=4,FC=2,则△DEF的周长是 .
16. 抛物线和x轴有公共点,则k的取值范围是 .17. 把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF,若BF=4,FC=2,则△DEF的周长是 . 18. 如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线y=x相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , ⋅⋅⋅,rn,则当r1=1时,r2022= .
18. 如图,圆心都在x轴正半轴上的半圆O1 , 半圆O2 , …,半圆On与直线y=x相切.设半圆O1 , 半圆O2 , …,半圆On的半径分别是r1 , r2 , ⋅⋅⋅,rn,则当r1=1时,r2022= .
三、解答题
-
19. 计算:(1)、;(2)、 .20. 某校组建了射击兴趣小组,甲、乙两人连续8次射击成绩如下列图、表所示(统计图中乙的第8次射击成绩缺失).

甲、乙两人连续射击8次成绩统计表
平均成绩(环)
中位数(环)
方差(环2)
甲
7.5
乙
6
3.5
(1)、乙的第8次射击成绩是环;(2)、补全统计图;(3)、如果你是教练,要从甲、乙两人中选一位参加比赛,你会选择谁?写出你这样选择的2条理由.21. 如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=8km.有一艘小船在点P处,从A处测得小船P在北偏西60的方向,从B处测得小船P在北偏东45°的方向.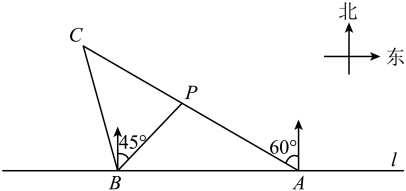 (1)、求点P到海岸线l的距离(结果保留根号);(2)、小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(结果精确到0.1km, , )22. 农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
(1)、求点P到海岸线l的距离(结果保留根号);(2)、小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(结果精确到0.1km, , )22. 农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:销售价格x(元/千克)
日销售量p(千克)
(1)、请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;(2)、农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?23. 如图所示,AB为⊙O的直径,在△ABC中,AB=BC,AC交⊙O于点D,过点D作DE⊥BC,垂足为点E. (1)、证明DE是⊙O的切线;(2)、AD=8,P为⊙O上一点,P到弦AD的最大距离为8.
(1)、证明DE是⊙O的切线;(2)、AD=8,P为⊙O上一点,P到弦AD的最大距离为8.①尺规作图作出此时的P点,保留作图痕迹;
②求DE的长.
24. 如图,在矩形ABCD中,AB=3,BC=5,BE平分∠ABC交AD于点E.连接CE,点F是BE上一动点,过点F作FG∥CE交BC于点G.将△BFG绕点B旋转得到△BF'G'. (1)、如图1,连接CG′,EF′,求证:△BEF′∽△BCG′;(2)、当点G'恰好落在直线AE上时,若BF=3,求EG'的值.25. 如图,抛物线经过 , , 三点.
(1)、如图1,连接CG′,EF′,求证:△BEF′∽△BCG′;(2)、当点G'恰好落在直线AE上时,若BF=3,求EG'的值.25. 如图,抛物线经过 , , 三点. (1)、求出抛物线的解析式;(2)、P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)、若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得 , 直接写出点D坐标.
(1)、求出抛物线的解析式;(2)、P是抛物线在第一象限上的一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)、若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得 , 直接写出点D坐标.