山东省滨州市2022年中考数学模拟试题

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $3 - (- 2)$ 的结果是（）

A、 $- 5$ B、 $- 1$ C、 $1$ D、5

查看试题解析
2. 下列运算正确的是（　　）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $(a^{2})^{3} = a^{6}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $2^{- 3} = - 6$

查看试题解析
3. 将甲乙两数据进行比较，如果甲的波动性大，那么（　　）

A、甲的标准差小 B、乙的方差小 C、甲的平均数大 D、乙的中位数小

查看试题解析
4. 下列根据等式基本性质变形正确的是（）

A、由 $- \frac{1}{3} x = \frac{2}{3} y$ ，得x=2y B、由3x-5=7，得3x=7-5 C、由2x-3=3x，得x=3 D、由3x-2=2x+2，得x=4

查看试题解析
5. 将不等式3x-2＜1的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 关于x的一元二次方程 $a {(x + 2)}^{2} + 2 = 0$ 的解的情况是（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
7. 已知四边形 $A B C D$ ，以下有四个条件.能判四边形 $A B C D$ 是平行四边形的有（）

A、 $A B / / C D$ ， $A D = B C$ B、 $A B = A D$ ， $B C = C D$ C、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ D、 $A B / / C D$ ， $A D / / B C$

查看试题解析
8. 关于下列说法：（1）反比例函数 $y = \frac{1}{3 m x}$ ，在每个象限内y随x的增大而减小；（2）函数 $y = - \frac{1}{3} x$ ， y随x的增大减小；（3）函数 $y = - \frac{1}{3} x^{2}$ ，当 $x > 0$ 时，y随x的增大而减小，其中正确的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 如图，已知□ABCD的对角线BD=4cm，将□ABCD绕其对称中心O旋转180°，则点D所转过的路径长为（）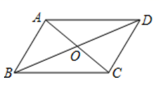

A、4π cm B、3π cm C、2π cm D、π cm

查看试题解析
10. 如图，AD $∥$ BE，AC与BC相交于点C，且∠1＝ $\frac{2}{n - 1}$ ∠DAB，∠2＝ $\frac{2}{n - 1}$ ∠EBA．若∠C＝45°，则n＝（　　）

A、7 B、8 C、9 D、10

查看试题解析
11. 对于反比例函数y $= \frac{k}{x}$ ，当x＞0时，y随x的增大而增大，则二次函数y＝-kx²-kx的大致图象是（　　）

A、 B、 C、 D、

查看试题解析
12. 如图，△ABC中，∠C=70°，⊙O切CA、CB分别于点A和点B，则弦AB所对的圆周角的度数为（）

A、110° B、55° C、55°或110° D、55或125°

查看试题解析

二、填空题

13. 函数 $y = \frac{\sqrt{x - 1}}{x - 2}$ 在实数范围内有意义的条件是．

查看试题解析
14. 如图，在等腰三角形 $A B C$ 中， $A B = A C = 5$ ，底边 $B C = 6$ ，则底角的余弦值为．

查看试题解析
15. 如图，在▱ABCD中，BC=2AB，CE⊥AB于E，F为AD的中点，若∠AEF=54°，
则∠B= ．

查看试题解析
16. 如图，点P在函数 $y = \frac{4 \sqrt{3}}{x} (x > 0)$ 的图象上运动，O为坐标原点，点A为 $P O$ 的中点，以点P为圆心， $P A$ 为半径作 $⊙ P$ ，则当 $⊙ P$ 与坐标轴相切时，点P的坐标为．

查看试题解析
17. 如果代数式 $a^{2} + 2 a$ 的值为 $5$ ，那么代数式 $3 - 4 a - 2 a^{2}$ 的值为．

查看试题解析
18.
如图，矩形ABCD中，点E、F分别是AB、CD的中点，连接DE和BF，分别取DE、BF的中点M、N，连接AM、CN、MN．若AB=3 $\sqrt{2}$ ， BC=2 $\sqrt{3}$ ，则图中阴影部分的面积为　．

查看试题解析

三、解答题

19. 计算： $| 1 - \sqrt{2} | - 2 s i n 4 5^{°} + (\frac{1}{2})^{- 1} + (π - 2021)^{0}$ ．

查看试题解析
20. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线 $A D$ 的两侧，且 $A E = D F$ ， $∠ A = ∠ D$ ， $A B = D C$ ．

(1)、求证：四边形 $B F C E$ 是平行四边形；

(2)、如果 $A D = 7$ ， $D C = 2$ ， $∠ E B D = 60 °$ ，那么当四边形 $B F C E$ 为菱形时 $B E$ 的长是多少？

查看试题解析
21. 某校兴趣小组就“最想去的漳州5个最美乡村”随机调查了本校部分学生. 要求每位同学选择且只能选择一个最想去的最美乡村. 下面是根据调查结果绘制出的尚不完整统计表和统计图，其中x、y是满足x<y的正整数.
最美乡村意向统计表
最美乡村
人数
A：龙海埭美村
10
B：华安官畬村
11
C：长泰山重村
4x
D：南靖塔下村
9
E：东山澳角村
3y
最美乡村意向扇形统计图
根据以上信息，解答下列问题：

(1)、求x、y的值；

(2)、若该校有1200名学生，请估计“最想去华安官畬村”的学生人数.

查看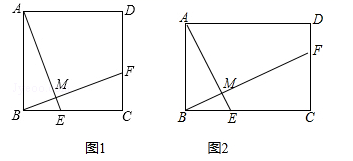试题解析
22.

(1)、如图1，在正方形ABCD中，点E ， F分别在BC ， CD上，AE⊥BF于点M ，求证：AE=BF；

(2)、如图2，将（1）中的正方形ABCD改为矩形ABCD ， AB=2，BC=3，AE⊥BF于点M ，探究AE与BF的数量关系，并证明你的结论．

查看试题解析
23. 重庆潼南某一蔬菜种植基地种植的一种蔬菜，它的成本是每千克 $2$ 元，售价是每千克 $3$ 元，年销量为 $10$ 万千克 $．$ 多吃绿色蔬菜有利于身体健康，因而绿色蔬菜倍受欢迎，十分畅销．为了获得更好的销量，保证人民的身体健康，基地准备拿出一定的资金作绿色开发，根据经验，若每年投入绿色开发的资金X万元，该种蔬菜的年销量将是原年销量的m倍，它们的关系如下表：
x万元
$0$
$1$
$2$
$3$
$4$
$\dots$
m
$1$
$1.5$
$1.8$
$1.9$
$1.8$
$\dots$

(1)、试估计并验证m与x之间的函数类型并求该函数的表达式；

(2)、若把利润看着是销售总额减去成本费和绿色开发的投入资金，试求年利润W万元与绿色开发投入的资金x万元的函数关系式；并求投入的资金不低于 $3$ 万元，又不超过 $5$ 万元时，x取多少时，年利润最大，求出最大利润．

(3)、基地经调查：若增加种植人员的奖金，从而提高种植积极性，又可使销量增加，且增加的销量y万千克与增加种植人员的奖金 $z$ 万元之间满足 $y = - z^{2} + 4 z$ ，若基地将投入 $5$ 万元用于绿色开发和提高种植人员的奖金，应怎样分配这笔资金才能使年利润达到 $17$ 万元且绿色开发投入大于奖金？ $\sqrt{2} = 1.4 ．$

查看试题解析
24. 抛物线y＝ax²+bx+c与x轴交于点A（1，0）和点B（5，0），与y轴交于点C（0，3）．该抛物线与直线y= $\frac{3}{5} x + c$ 相交于C，D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M，N．

(1)、求该抛物线所对应的函数解析式；

(2)、连结PC，PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；

(3)、连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．

查看试题解析

最美乡村	人数
A：龙海埭美村	10
B：华安官畬村	11
C：长泰山重村	4x
D：南靖塔下村	9
E：东山澳角村	3y

x万元	$0$	$1$	$2$	$3$	$4$	$\dots$
m	$1$	$1.5$	$1.8$	$1.9$	$1.8$	$\dots$