山东省滨州市2022年中考数学考前模拟冲刺试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 数轴上标出若干个点,每相邻两点相距一个单位长度,点A、B,C,D分别表示整数a,b,c,d,且a+b+c+d=6,则点D表示的数为( )
 A、-2 B、0 C、3 D、52. 如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A、-2 B、0 C、3 D、52. 如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( ) A、2m B、3m C、6m D、9m3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形中,的平分线交于E, , , 则的长( )
A、2m B、3m C、6m D、9m3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,平行四边形中,的平分线交于E, , , 则的长( ) A、4 B、5 C、5.5 D、65. 如图是由4个相同的小正方体成的物体,将它在水平面内顺时针旋转90°后,其主视图是( )
A、4 B、5 C、5.5 D、65. 如图是由4个相同的小正方体成的物体,将它在水平面内顺时针旋转90°后,其主视图是( )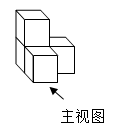 A、
A、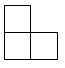 B、
B、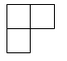 C、
C、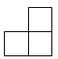 D、
D、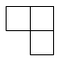 6. 不等式组的解集,在数轴上表示正确的是( )A、
6. 不等式组的解集,在数轴上表示正确的是( )A、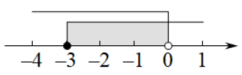 B、
B、 C、
C、 D、
D、 7. 一元二次方程 根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根8. 有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )A、 B、 C、 D、9. 如图所示,已知 是 的外接圆, 是 的直径,连接 ,若 , 则 的值为( )
7. 一元二次方程 根的情况是( )A、只有一个实数根 B、有两个相等的实数根 C、没有实数根 D、有两个不相等的实数根8. 有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )A、 B、 C、 D、9. 如图所示,已知 是 的外接圆, 是 的直径,连接 ,若 , 则 的值为( ) A、 B、 C、 D、10. 已知两条抛物线P和Q的解析式分别是关于y与x的关系式:P:与Q: . 对上述抛物线说法正确的序号是( )
A、 B、 C、 D、10. 已知两条抛物线P和Q的解析式分别是关于y与x的关系式:P:与Q: . 对上述抛物线说法正确的序号是( )①两条抛物线与y轴的交点一定不在x轴的上方;
②在抛物线P、Q中,可以将其中一条抛物线经过向上或向下平移得到另一条抛物线;
③在抛物线P、Q中,可以将其中一条抛物线经过向左或向右平移得到另一条抛物线;
④两条抛物线的顶点之间的距离为1.
A、①② B、①③④ C、①②④ D、①②③④11. 互不重合的两点 , 皆落于反比例函数图象上,当直线AB与第二象限角平分线垂直时,的值等于( )A、 B、1 C、 D、712. 如图,△ABC中,∠ACB=90°,AC=BC,AB=10 , 点G为AC中点,连接BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH,以下结论:①∠ACE=∠ABG;②CF=;③∠AGE=∠CGB;④FH平分∠BFE,其中正确的结论有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
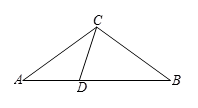
13. 若式子在实数范围内有意义,则x的取值范围是.14. 如图,在 中, ,点D在AB上,若 , ,则 .
 15. 计算: .16. 已知一组数据分别为:93,93,88,81,94,91,则这组数据的方差为 .17. 函数y 的定义域是 .18. 如图,点O为等边内一点, , , 连接并延长交于点D.若 , 过点B作交延长线于点F,连接 , 则 .
15. 计算: .16. 已知一组数据分别为:93,93,88,81,94,91,则这组数据的方差为 .17. 函数y 的定义域是 .18. 如图,点O为等边内一点, , , 连接并延长交于点D.若 , 过点B作交延长线于点F,连接 , 则 .
三、解答题
-
19. 计算: .20. 某国产著名品牌衬衫标价为400元/件,去年中秋节和国庆节期间经过两次优惠降价为324元 /件,并且两次降价的百分率相同:(1)、求该种衬衫每次降价的百分率;(2)、若该种品牌衬衫的进价为300元/件,两次降价共售出此种品牌衬衫100件,为使两次降价销售的总利润不少于3120元,第一次降价至少要销售出多少件该种衬衫?21. 将两张完全相同的矩形纸片 ,矩形纸片 按如图方式放置, 为重合的对角线,重叠部分为四边形 .
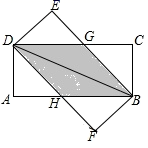 (1)、试判断四边形 为何种特殊的四边形,并说明理由;(2)、若四边形 的面积为15, ,求 的长.22. 为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过 时,水费按每立方米1.1元收费,超过 时,超过部分每立方米按1.6元收费,设每户每月用水量为 ,应缴水费为y元.(1)、写出y与x之间的函数表达式;(2)、如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?23. 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
(1)、试判断四边形 为何种特殊的四边形,并说明理由;(2)、若四边形 的面积为15, ,求 的长.22. 为了加强公民的节水意识,某地规定用水收费标准如下:每户每月用水量不超过 时,水费按每立方米1.1元收费,超过 时,超过部分每立方米按1.6元收费,设每户每月用水量为 ,应缴水费为y元.(1)、写出y与x之间的函数表达式;(2)、如果有两户家庭某月份需缴纳水费为5.5元和9.8元时,求这两户家庭这个月的用水量分别是多少?23. 如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE. (1)、求证:AD∥BC;(2)、过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC的长.24. 如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B , 抛物线y=﹣x2+bx+c经过点A , B .
(1)、求证:AD∥BC;(2)、过点C作CG⊥AD于点F,交AE于点G,若AF=4,求BC的长.24. 如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B , 抛物线y=﹣x2+bx+c经过点A , B . (1)、求抛物线的解析式.(2)、M是抛物线对称轴上的一点连接BM , CM , 求BM+CM的最小值.(3)、若E(m , 0)为x轴正半轴上一动点,过点E作直线ED⊥x轴,交直线AB于点D , 交抛物线于点P , 连接BP , BC , 当∠PBD+∠CBO=45°时,请求出m的值.
(1)、求抛物线的解析式.(2)、M是抛物线对称轴上的一点连接BM , CM , 求BM+CM的最小值.(3)、若E(m , 0)为x轴正半轴上一动点,过点E作直线ED⊥x轴,交直线AB于点D , 交抛物线于点P , 连接BP , BC , 当∠PBD+∠CBO=45°时,请求出m的值.