山东省滨州市惠民县2022年中考二模数学试题

试卷更新日期：2023-03-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，所给三视图的几何体是（）

A、球 B、圆柱 C、圆锥 D、三棱锥

查看试题解析
2. 若a，b为非零实数，且 $a > b$ ，则下列结论一定正确的是（　　）

A、 $a^{2} > b^{2}$ B、 $a^{- 1} > b^{- 1}$ C、 $a^{3} > b^{3}$ D、 $a^{- 1} < b^{- 1}$

查看试题解析
3. 若 $m + \frac{1}{m} = 3$ ，则 $\frac{1}{2} m^{2} - \frac{3}{2} m + 1$ 的值是（　　）

A、2 B、0 C、 $\frac{3}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 在矩形ABCD中， $A B = 5$ ， $A D = 6$ ，动点P满足 $S_{△ P A B} = \frac{1}{6} S_{矩形 A B C D}$ ，则点P到A，B两点距离之和最小值为（）

A、 $\sqrt{61}$ B、 $\sqrt{41}$ C、 $\sqrt{29}$ D、 $\sqrt{26}$

查看试题解析
5. 若函数 $y = k x + 1$ 的图象经过第一、二、四象限，且与x轴的交点位于（1，0）点和（2，0）点之间，则k的取值范围是（　　）

A、 $- 1 < k < - \frac{1}{2}$ B、 $k < 0$ C、 $- \frac{1}{2} < k < 0$ D、 $k < - 1$

查看试题解析
6. 如图，按照程序图计算，当输入正整数x时，输出的结果是215，则输入的x的值可能（）

A、6 B、7 C、8 D、9

查看试题解析
7. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH， $E H = 3 c m$ ， $E F = 4 c m$ ，则边AB的长度等于（）

A、4cm B、4.2cm C、4.8cm D、5cm

查看试题解析
8. 如图，函数 $y = 2 x$ 与函数 $y = \frac{2}{x}$ 的图象交于A，B两点，点P在以C(-2，0)为圆心，1为半径的圆C上，Q是AP的中点，则OQ长的最大值为（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\sqrt{5}$ D、 $\sqrt{5} + 1$

查看试题解析

二、多选题

9. 抽查部分用户的用电量，统计数据如图所示，横轴为用电量（单位：千瓦时），纵轴为户数，关于这些用户的用电量的描述正确的是（）

A、中位数是40 B、平均值是42.6 C、众数是45 D、每户的用电量都增加10千瓦时，其方差也会增加10

查看试题解析
10. 下列关于x的方程 $a x^{2} + (a - 1) x - \frac{1}{4} = 0$ 的说法正确的是（　　）

A、一定有两个实数根 B、可能只有一个实数根 C、可能无实数根 D、当 $a < 0$ 时，方程有两个负实数根

查看试题解析
11. 如图，AB是圆O的直径，点G是圆上任意一点，点C是 $\overset{⌢}{B G}$ 的中点， $C D ⊥ A B$ ，垂足为点E，连接GA，GB，GC，GD，BC，GB与CD交于点F，则下列表述正确的是（）

A、 $∠ A B C = ∠ A G D$ B、 $△ B C E ∽ △ A B G$ C、 $G F = D F$ D、 $B C ∥ G D$

查看试题解析
12. 如图是抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点是B（4，0），点P在抛物线上，且在直线AB上方，则下列结论正确的是（）

A、 $a b c > 0$ B、方程 $a x^{2} + b x + c = 3$ 有两个相等的实根 C、 $x (a x + b) ⩽ a + b$ D、点P到直线AB的最大距离 $\frac{3 \sqrt{2}}{8}$

查看试题解析

三、填空题

13. 如图，在过点 $P$ 作直线 $a$ 的垂线时，小颖先将一圆形透明纸片对折得到折痕 $A B$ ，然后让端点 $A$ 与点 $P$ 重合，端点 $B$ 落在直线 $a$ 上，标出直线 $a$ 与圆形纸片的交点 $C$ ，连接 $A C$ ，则 $A C ⊥ a$ ．她的作图依据是．

查看试题解析
14. 如图，A，B是反比例函数 $y = \frac{k}{x} (k > 0)$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4， $S_{△ A O B} = 3$ ，则k的值为．

查看试题解析
15. 如图①，在平行四边形ABCD中， $∠ B = 120 °$ ，点P沿B→C→D→A运动到点A处停止．设点P的运动路程为xcm， $△ P A B$ 的面积为ycm² ， y与x之间的函数关系用图②来表示，则平行四边形ABCD的面积为．

查看试题解析
16. 抛物线 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 的图象如图所示，点A₁ ， A₂ ， A₃ ， A₄…，A₂₀₂₂在抛物线第一象限的图象上，点B₁ ， B₂ ， B₃ ， B₄^. ．．，B₂₀₂₂在y轴的正半轴上， $△ O A_{1} B_{1}$ 、 $△ B_{1} A_{2} B_{2}$ 、…、 $△ B_{2021} A_{2022} B_{2022}$ 都是等腰直角三角形，则 $B_{2021} A_{2022} =$ ．

查看试题解析

四、解答题

17. 我们初中学习的频数直方图是用纵轴表示频数，如果现在我们改用纵轴表示 $\frac{频率}{组距}$ ，（如第一组[50，60）表示数据小于60但不小于50，组距为60-50＝10），这时每个小矩形的面积就是该组内数据的频率，这种图形称为频率分布直方图．从某校初三一班的一次数学测试成绩中随机抽取了部分学生成绩，制作了统计表和频率分布直方图，后来都受到污损，如图所示，根据以上信息，回答下列问题：
分组
频数
[50，60）
2
[60，70）
[70，80）
10
[80，90）
7
[90，100）
2

(1)、求该样本的样本容量；

(2)、计算频率分布直方图中，从左到右第三个矩形的高度；

(3)、从分数在[50，70）间的试卷中，随机抽取两份分析学生成绩，求至少有一份分数在[50，60）间的概率．

查看试题解析
18. 无锡水蜜桃享誉海内外，老王用3000元购进了一批水蜜桃.第一天，很快以比进价高40% 的价格卖出150千克.第二天，他发现剩余的水蜜桃卖相已不太好，于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出，本次生意老王一共获利750元.

(1)、求这批水蜜桃进价为多少元？

(2)、老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克，第二天，老王把卖相不好的水蜜桃挑出，单独打折销售，售价为10元/千克，结果很快被一抢而空，其余的仍按第一天的价格销售，且当天全部售完.若老王这次至少获利1000元，请问打折销售的水蜜桃最多多少千克？（精确到1千克.）

查看试题解析
19. 如图1的风力发电机，风轮的三个叶片均匀分布，当风轮的叶片在风力作用下旋转时，最高点距地面 $145 m$ ，最低点距地面 $55 m$ ．如图2是该风力发电机的示意图，发电机的塔身 $O D$ 垂直于水平地面 $M N$ （点 $O$ ， $A$ ， $B$ ， $C$ ， $D$ ， $M$ ， $N$ 在同一平面内）．

(1)、求风轮叶片 $O A$ 的长度；

(2)、如图2，点 $A$ 在 $O D$ 右侧，且 $α = 14.4 °$ ．求此时风叶 $O B$ 的端点 $B$ 距地面的高度．（参考数据： $s i n 44.4 ° \approx 0.70$ ， $t a n 44.4 ° \approx 0.98$ ）

查看试题解析
20. 要建设六间长方形鸡舍，如图是其平面示意图，一面靠墙，其余各面用铁丝网围成．设每间鸡舍的长为xm，宽为ym．

(1)、现有长度为144m的铁丝网，受地形影响要求 $15 \leq x \leq 18$ ，如何设计可使每间鸡舍面积最大？（建设过程中的损耗忽略不计）

(2)、若使每间鸡舍面积为200m² ，每间鸡舍的长、宽各设计为多少时，可使围成鸡舍的铁丝网总长度最小？（精确到0.1m， $\sqrt{3} \approx 1.732$ ）

查看试题解析
21. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $⊙ O$ 与 $B C$ ， $A C$ 分别相切于点E，F， $B O$ 平分 $∠ A B C$ ，连接 $O A$ .

(1)、求证： $A B$ 是 $⊙ O$ 的切线；

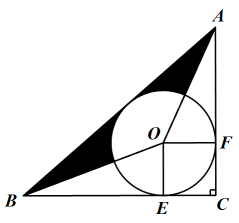(2)、若 $B E = A C = 3$ ， $⊙ O$ 的半径是1，求图中阴影部分的面积.

查看试题解析
22. 如图，抛物线 $y = a x^{2} + b x + 3$ （a，b是常数，且 $a \neq 0$ ）与x轴交于A，B两点，与y轴交于点C．并且A，B两点的坐标分别是 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ．

(1)、求抛物线的函数表达式；

(2)、点P是第一象限内抛物线上的动点，是否存在点P，使得 $△ P B C$ 是直角三角形？若存在，求点P的横坐标；若不存在，请说明理由；

(3)、点F在抛物线的对称轴上，若线段FB绕点F逆时针旋转 $90 °$ 后，点B的对应点B'恰好也落在此抛物线上，请直接写出点F的坐标．

查看试题解析
23.

(1)、【问题情境】
如图1，在正方形ABCD中，E，F，G分别是BC，AB，CD上的点，FG⊥AE于点Q．求证：AE＝FG．

(2)、【尝试应用】
如图2，正方形网格中，点A，B，C，D为格点，AB交CD于点O．求tan∠AOC的值；

(3)、【拓展提升】
如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交线段BC，PC于点M，N．
①求∠DMC的度数；
②连接AC交DE于点H，直接写出 $\frac{D H}{B C}$ 的值．

查看试题解析

分组	频数
[50，60）	2
[60，70）
[70，80）	10
[80，90）	7
[90，100）	2