青海省西宁市2022年中考一模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 下列四个数中,负整数是( )A、 B、 C、0 D、2. 2021年5月国家统计局公布了第七次人口普查结果,我国人口数约为1412000000,其中数据1412000000用科学记数法表示为( )A、 B、 C、 D、3. 下列各式中,正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、任意掷一枚质地均匀的骰子,掷出的点数一定是奇数 B、“从一副扑克牌中任意抽取一张,抽到红桃”是必然事件 C、了解一批冰箱的使用寿命,采用抽样调查的方式 D、平均数相同的甲、乙两组数据的方差: , , 则甲组数据更稳定5. 已知一次函数的图象过点 , 则下列结论正确的是( )A、 B、y随x增大而增大 C、图象不经过第一象限 D、函数的图象一定经过点6. 甲、乙两人沿着长为的“健身步道”同时出发健步走,甲的速度是乙的速度的1.2倍,甲比乙提前12分钟走完全程.设乙的速度为 , 则可列方程为( )A、 B、 C、 D、7. 如图,在中, , 以B为圆心,适当长为半径画弧,分别交于点M,N,分别以M,N为圆心,大于的长为半径画弧,两弧在内部交于点D,作射线BD交AC于点E,点F为BC的中点,连接EF.若 , 则的周长为( )
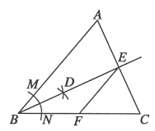 A、 B、 C、 D、48. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( )
A、 B、 C、 D、48. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、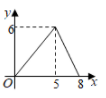 B、
B、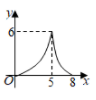 C、
C、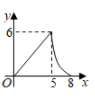 D、
D、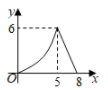
二、填空题
-
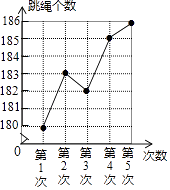
9. .10. 函数 中,自变量 的取值范围是.11. 不等式组 , 的解集是 .12. 某同学在体育训练中统计了自己五次“1分钟跳绳”成绩,并绘制了如图所示的折线统计图,这五次“1分钟跳绳”成绩的中位数是个.
 13. 已知m,n是一元二次方程的两个根,则 .14. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为 .
13. 已知m,n是一元二次方程的两个根,则 .14. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为 . 15. 如图,面积为16的正方形内接于 , 则的长为 .
15. 如图,面积为16的正方形内接于 , 则的长为 .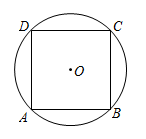 16. 矩形的周长等于40,则此矩形面积的最大值是 .17. 已知点A为直线上一点,过点A作轴,交双曲线于点B.若点A与点B关于y轴对称,则点A的坐标为 .18. 二次函数图象的一部分如图所示.已知图象经过点 , 对称轴为直线 . 下列结论:①;②;③若抛物线经过点 , 则关于x的一元二次方程的两根分别是;其中正确结论的序号是 .
16. 矩形的周长等于40,则此矩形面积的最大值是 .17. 已知点A为直线上一点,过点A作轴,交双曲线于点B.若点A与点B关于y轴对称,则点A的坐标为 .18. 二次函数图象的一部分如图所示.已知图象经过点 , 对称轴为直线 . 下列结论:①;②;③若抛物线经过点 , 则关于x的一元二次方程的两根分别是;其中正确结论的序号是 .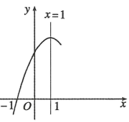
三、解答题
-
19. 计算:20. 解方程 .21. 先化简,再求值: ,其中 .22. 在三张形状、大小、质地都相同的卡片上各写一个数字,分别为 , , , 现将三张卡片放入一个不透明的盒子中,搅匀后任意抽出一张,记下数字后放回,搅匀后再任意抽出一张记下数字.(1)、第一次抽到写有正数的卡片的概率是;(2)、用画树状图或列表的方法求两次抽出的卡片上数字之积为有理数的概率,并列出所有等可能的结果.23. 如图, 与 交于点O, ,E为 延长线上一点,过点E作 ,交 的延长线于点F.
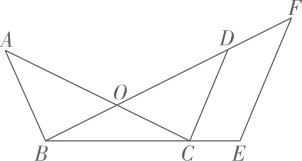 (1)、求证 ;(2)、若 ,求 的长.24. 如图,在平面直角坐标系中,矩形的顶点A,C分别在x轴,y轴上,D是BC的中点,过点D的反比例函数的图象交AB于点E,连接DE.若 , .
(1)、求证 ;(2)、若 ,求 的长.24. 如图,在平面直角坐标系中,矩形的顶点A,C分别在x轴,y轴上,D是BC的中点,过点D的反比例函数的图象交AB于点E,连接DE.若 , .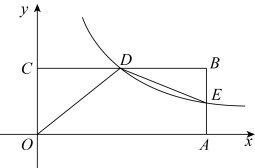 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且以P,A,E为顶点的三角形是等腰直角三角形,请直接写出P点坐标.25. 如图,在Rt△ACD中,∠ACD=90°,点O在CD上,作⊙O,使⊙O与AD相切于点B,⊙O与CD交于点E,过点D作DF∥AC,交AO的延长线于点F,且∠OAB=∠F.
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且以P,A,E为顶点的三角形是等腰直角三角形,请直接写出P点坐标.25. 如图,在Rt△ACD中,∠ACD=90°,点O在CD上,作⊙O,使⊙O与AD相切于点B,⊙O与CD交于点E,过点D作DF∥AC,交AO的延长线于点F,且∠OAB=∠F.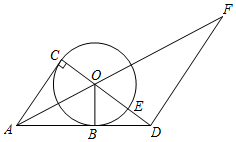 (1)、求证:AC是⊙O的切线;(2)、若OC=3,DE=2,求tan∠F的值.26. 如图1,在△ABC中,D为BC的中点,求证:AB+AC>2AD.
(1)、求证:AC是⊙O的切线;(2)、若OC=3,DE=2,求tan∠F的值.26. 如图1,在△ABC中,D为BC的中点,求证:AB+AC>2AD.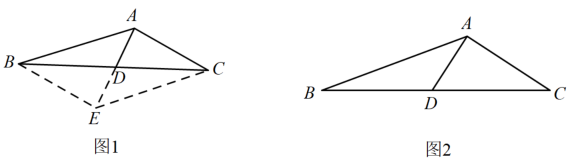 (1)、甲说:不可能出现 , 所以此题无法解决;
(1)、甲说:不可能出现 , 所以此题无法解决;乙说:我们可以延长AD至点E,使得 , 连接 , 因为 , 就可以直接得到四边形是平行四边形.请写出此处的依据:(平行四边形判定的文字描述).所以 , 在中, , 即 .
(2)、请根据乙提供的思路解决下列问题:如图2,在△ABC中,D为BC的中点,AB=5,AC=3,AD=2.求△ABC的面积.
27. 如图,抛物线与x轴交于点和点B,与y轴交于点 , 顶点为点D,直线是抛物线的对称轴,且与直线BC交于点E.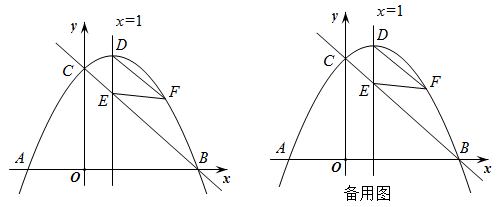 (1)、求抛物线的解析式;(2)、点F是直线BC上方抛物线上的一点,连接 , 若的面积等于 , 求点F的坐标;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D,E,P,Q为顶点的四边形是平行四边形,求点P的坐标.
(1)、求抛物线的解析式;(2)、点F是直线BC上方抛物线上的一点,连接 , 若的面积等于 , 求点F的坐标;(3)、平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D,E,P,Q为顶点的四边形是平行四边形,求点P的坐标.