青海省西宁市2022年中考二模数学试题
试卷更新日期:2023-03-27 类型:中考模拟
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、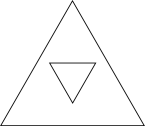 C、
C、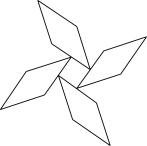 D、
D、 2. 下列命题是真命题的是( )A、两点之间直线最短 B、多边形的外角和为360° C、三角形的任意两边之和小于第三边 D、直角三角形的两个锐角互补3. 如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则( )
2. 下列命题是真命题的是( )A、两点之间直线最短 B、多边形的外角和为360° C、三角形的任意两边之和小于第三边 D、直角三角形的两个锐角互补3. 如图是一个正方体的表面展开图,这个正方体相对表面上所标的数字相等,则( ) A、-5 B、-1 C、0 D、44. 下列计算中,正确的是( )A、 B、 C、 D、5. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、116. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差7. 已知二次函数的图像如图所示,则一次函数的图像和反比例函的图像在同一坐标系中大致是( )
A、-5 B、-1 C、0 D、44. 下列计算中,正确的是( )A、 B、 C、 D、5. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、116. “红色小讲解员”演讲比赛中,7位评委分别给出某位选手的原始评分.评定该选手成绩时,从7个原始评分中去掉一个最高分、一个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,这两组数据一定不变的是( ).A、中位数 B、众数 C、平均数 D、方差7. 已知二次函数的图像如图所示,则一次函数的图像和反比例函的图像在同一坐标系中大致是( )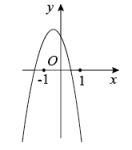 A、
A、 B、
B、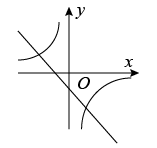 C、
C、 D、
D、 8. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( )
8. 如图,抛物线 与 轴只有一个公共点A(1,0),与 轴交于点B(0,2),虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
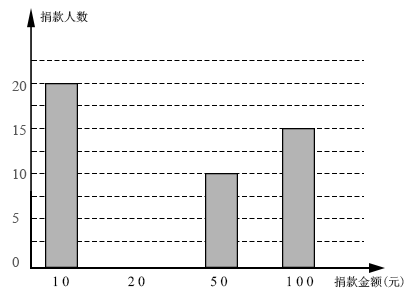
9. 比较大小:-3-4.10. 请写出一个无理数 .11. 新型冠状病毒的直径是0.00012mm.将0.00012用科学记数表示是 .12. 分解因式 .13. 计算: .14. 在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐10元的人数占年级总人数的25%,则本次捐款的总人数为人.
 15. 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数的图象经过点D,则反比例函数的解析式是 .
15. 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数的图象经过点D,则反比例函数的解析式是 . 16. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,则桥AB的长度是米(结果保留根号).
16. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,则桥AB的长度是米(结果保留根号).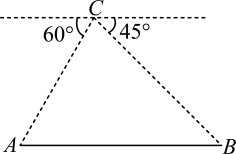 17. 如图,矩形AOBC的顶点A,B在坐标轴上,点C的坐标是(-10,8),点D在AC上,将沿BD翻折,点C恰好落在OA边上点E处,则D点坐标是 .
17. 如图,矩形AOBC的顶点A,B在坐标轴上,点C的坐标是(-10,8),点D在AC上,将沿BD翻折,点C恰好落在OA边上点E处,则D点坐标是 .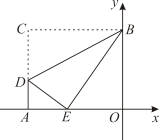 18. 如图,在平面直角坐标系中,点A是函数图像上的一个动点,⊙A的半径长为1.已知点B(-4,0),连接AB.当⊙A与两坐标轴同时相切时,的值是 .
18. 如图,在平面直角坐标系中,点A是函数图像上的一个动点,⊙A的半径长为1.已知点B(-4,0),连接AB.当⊙A与两坐标轴同时相切时,的值是 .
三、解答题
-
19. 计算:20. 计算: .21. 已知实数a,b满足 , 解关于x的一元二次方程 .22. 甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色相同,则甲获胜;若两次指针指到的颜色是黄绿组合则乙获胜;其余情况则视为平局.
 (1)、请用画树状图或列表的方法,写出所有可能出现的结果;(2)、试用概率说明游戏是否公平.23. 如图,在矩形ABCD中,点E在AB上,AB=DE,CF⊥DE,垂足为F.
(1)、请用画树状图或列表的方法,写出所有可能出现的结果;(2)、试用概率说明游戏是否公平.23. 如图,在矩形ABCD中,点E在AB上,AB=DE,CF⊥DE,垂足为F.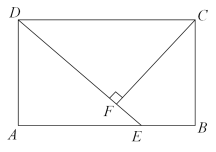 (1)、求证:CF=CB;(2)、若∠FCB=30°,且AD=2,求EF的长.24. 小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.(1)、求买一支康乃馨和一支百合各需多少元?(2)、小美准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为w元,康乃馨有x支,求w与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.25. 如图, 是 的外接圆, 是 的直径, 于点 .
(1)、求证:CF=CB;(2)、若∠FCB=30°,且AD=2,求EF的长.24. 小美打算买一束百合和康乃馨组合的鲜花,在“母亲节”祝福妈妈.已知买2支百合和1支康乃馨共需花费14元,3支康乃馨的价格比2支百合的价格多2元.(1)、求买一支康乃馨和一支百合各需多少元?(2)、小美准备买康乃馨和百合共11支,且百合不少于2支.设买这束鲜花所需费用为w元,康乃馨有x支,求w与x之间的函数关系式,并设计一种使费用最少的买花方案,写出最少费用.25. 如图, 是 的外接圆, 是 的直径, 于点 .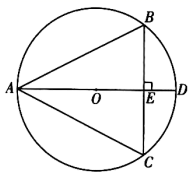 (1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.26. 用※定义一种新运算:对于任意实数m和n , 规定 ,如: .
(1)、求证: ;(2)、连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求 和 的长.26. 用※定义一种新运算:对于任意实数m和n , 规定 ,如: .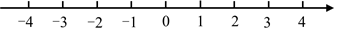 (1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.27. 如图①,抛物线与x轴交于A,B两点,与y轴交于点C(0,3),顶点为D(4,-1),对称轴与直线BC交于点E,与x轴交于点F.
(1)、求 ;(2)、若 ,求m的取值范围,并在所给的数轴上表示出解集.27. 如图①,抛物线与x轴交于A,B两点,与y轴交于点C(0,3),顶点为D(4,-1),对称轴与直线BC交于点E,与x轴交于点F.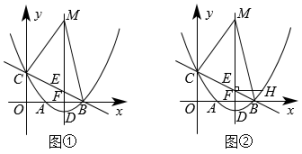 (1)、求二次函数的解析式;(2)、点M在第一象限抛物线的对称轴上,若点C在BM的垂直平分线上,求点M的坐标;(3)、如图②,过点E作对称轴的垂线在对称轴的右侧与抛物线交于点H,x轴上方的对称轴上是否存在一点P,使以E,H,P为顶点的三角形与相似,若存在,求出P点坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、点M在第一象限抛物线的对称轴上,若点C在BM的垂直平分线上,求点M的坐标;(3)、如图②,过点E作对称轴的垂线在对称轴的右侧与抛物线交于点H,x轴上方的对称轴上是否存在一点P,使以E,H,P为顶点的三角形与相似,若存在,求出P点坐标;若不存在,请说明理由.