冲刺2023中考——数学模拟考场仿真演练卷八
试卷更新日期:2023-03-26 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 已知实数 , 在数轴上的位置如图所示,则的值是( )
 A、-2 B、-1 C、0 D、22. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、
A、-2 B、-1 C、0 D、22. 下列分别是2022年北京冬奥会、1998年长野冬奥会、1992年阿尔贝维尔冬奥运会、1984年萨拉热窝冬奥会会徽上的图案,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 沿正方体相邻的三条棱的中点截掉一个角,得到如图所示的几何体,则他的主视图是( )
3. 沿正方体相邻的三条棱的中点截掉一个角,得到如图所示的几何体,则他的主视图是( )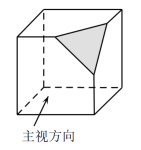 A、
A、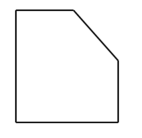 B、
B、 C、
C、 D、
D、 4. 无色酚酞溶液是一中常见常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色.现有5瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )A、 B、 C、 D、5. 下列运算正确的是( )A、3a﹣2a=a B、(a3)2=a5 C、2﹣=2 D、(a﹣1)2=a2﹣16. 下列说法正确的是( )
4. 无色酚酞溶液是一中常见常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸溶液不变色,遇中性溶液也不变色,遇碱溶液变红色.现有5瓶缺失标签的无色液体:蒸馏水、白醋溶液、食用碱溶液、柠檬水溶液、火碱溶液,将酚酞试剂滴入任意一瓶液体后呈现红色的概率是( )A、 B、 C、 D、5. 下列运算正确的是( )A、3a﹣2a=a B、(a3)2=a5 C、2﹣=2 D、(a﹣1)2=a2﹣16. 下列说法正确的是( )①若二次根式有意义,则x的取值范围是x≥1.
②7<<8.
③若一个多边形的内角和是540°,则它的边数是5.
④的平方根是±4.
⑤一元二次方程x2﹣x﹣4=0有两个不相等的实数根.
A、①③⑤ B、③⑤ C、③④⑤ D、①②④7. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( ) A、 B、 C、 D、8. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( )
A、 B、 C、 D、8. 如图,点E在矩形 的 边上,将 沿 翻折,点A恰好落在 边上的点F处,若 , ,则 的长为( ) A、9 B、12 C、15 D、189. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( )
A、9 B、12 C、15 D、189. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤10. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( )
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤10. 二次函数 的部分图象如图所示,与y轴交于 ,对称轴为直线 .下列结论:① ;② ;③对于任意实数m,都有 成立;④若 , , 在该函数图象上,则 ;⑤方程 ( ,k为常数)的所有根的和为4.其中正确结论有( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(每空3分,共18分)
-
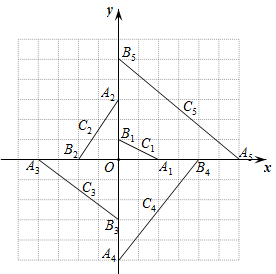
11. 已知 ,则 .12. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
 13. 如图,将绕点旋转得到 , 若 , , , 则 .
13. 如图,将绕点旋转得到 , 若 , , , 则 .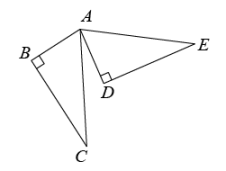 14. 如图,在中, , 以点A为圆心、为半径画弧交于点E,连接 , 若 , 则图中阴影部分的面积是.
14. 如图,在中, , 以点A为圆心、为半径画弧交于点E,连接 , 若 , 则图中阴影部分的面积是. 15. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .
15. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .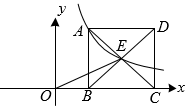 16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
三、解答题(共9题,共72分)
-
17. 先化简,再求值: , 其中是满足条件的合适的非负整数.18.(1)、计算:;(2)、解不等式组:19. 如图,在和中, , , , 且点D在线段上,连 .
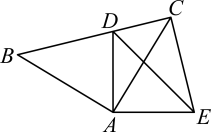 (1)、求证:;(2)、若 , 求的度数.20. 为提高学生的综合素养,某校开设了四个兴趣小组,A“健美操”、B“跳绳”、C“剪纸”、D“书法”为了了解学生对每个兴趣小组的喜爱情况,随机抽取了部分同学进行调查,并将调查结果绘制出上面不完整的统计图,请结合图中的信息解答下列问题:
(1)、求证:;(2)、若 , 求的度数.20. 为提高学生的综合素养,某校开设了四个兴趣小组,A“健美操”、B“跳绳”、C“剪纸”、D“书法”为了了解学生对每个兴趣小组的喜爱情况,随机抽取了部分同学进行调查,并将调查结果绘制出上面不完整的统计图,请结合图中的信息解答下列问题: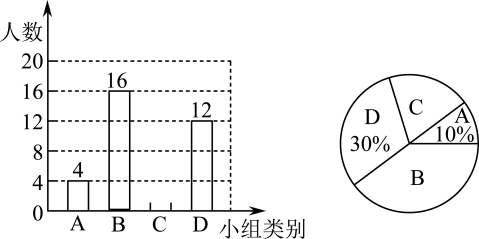 (1)、本次共调查了 ▲ 名学生;并将条形统计图补充完整;(2)、C组所对应的扇形圆心角为度;(3)、若该校共有学生1400人,则估计该校喜欢跳绳的学生人数约是;(4)、现选出了4名跳绳成绩最好的学生,其中有1名男生和3名女生.要从这4名学生中任意抽取2名学生去参加比赛,请用列表法或画树状图法,求刚好抽到1名男生与1名女生的概率.21. 对于一个各数位上的数字均不为 0 的三位自然数 N,若 N 能被它的各数位上的数字之和 m 整除,则称 N 是 m 的“和倍数”.
(1)、本次共调查了 ▲ 名学生;并将条形统计图补充完整;(2)、C组所对应的扇形圆心角为度;(3)、若该校共有学生1400人,则估计该校喜欢跳绳的学生人数约是;(4)、现选出了4名跳绳成绩最好的学生,其中有1名男生和3名女生.要从这4名学生中任意抽取2名学生去参加比赛,请用列表法或画树状图法,求刚好抽到1名男生与1名女生的概率.21. 对于一个各数位上的数字均不为 0 的三位自然数 N,若 N 能被它的各数位上的数字之和 m 整除,则称 N 是 m 的“和倍数”.例如:∵247÷(2+4+7)= 247÷13=19,∴247是13的“和倍数”.
又如: ∵214÷(2+1+4)=214÷7=30……4,∴214不是“和倍数”.
(1)、判断 357,441 是否是“和倍数”?说明理由;(2)、三位数 A是12的“和倍数”,a,b,c 分别是数 A其中一个数位上的数字,且 a>b>c在 a,b,c 中任选两个组成两位数,其中最大的两位数记为 F (A),最小的两位数记为 G(A),若 为整数,求出满足条件的所有数 A.22. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C. (1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.23. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC;
(1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.23. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线BO与双曲线在第一象限交于点C,连接AC; (1)、求直线AB与双曲线的解析式.(2)、求△ABC的面积24. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
(1)、求直线AB与双曲线的解析式.(2)、求△ABC的面积24. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .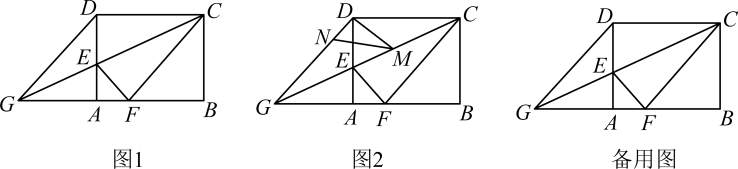 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.25. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.25. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.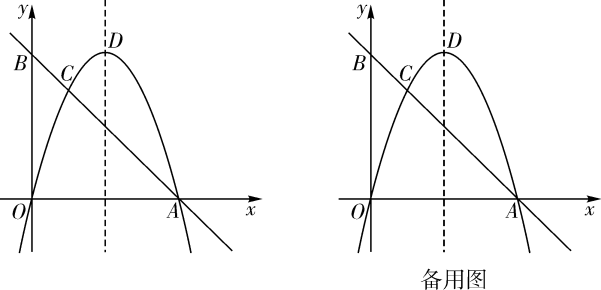 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.