冲刺2023中考——数学模拟考场仿真演练卷七
试卷更新日期:2023-03-24 类型:中考模拟
一、单选题(每题3分,共30分)
-
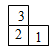
1. 用四舍五入法取近似值,将数0.0158精确到0.001的结果是( )A、0.015 B、0.016 C、0.01 D、0.022. 下面各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、3. 如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
 A、
A、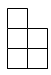 B、
B、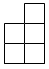 C、
C、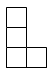 D、
D、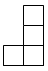 4. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
4. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )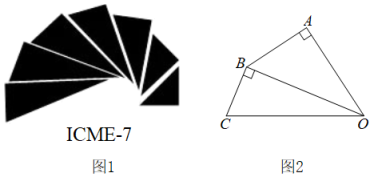 A、 B、 C、 D、15. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
A、 B、 C、 D、15. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )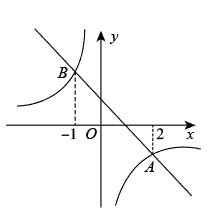 A、或 B、或 C、或 D、6. 某中学青年志愿者协会的10名志愿者,一周的社区志愿服务时间如下表所示:
A、或 B、或 C、或 D、6. 某中学青年志愿者协会的10名志愿者,一周的社区志愿服务时间如下表所示:时间/h
2
3
4
5
6
人数
1
3
2
3
1
关于志愿者服务时间的描述正确的是( )
A、众数是6 B、平均数是4 C、中位数是3 D、方差是17. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、208. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( ) A、25π+24 B、5π+24 C、25π D、5π9. 用配方法解方程x2+4x+1=0时,配方结果正确的是( )A、(x﹣2)2=5 B、(x﹣2) 2=3 C、(x+2) 2=5 D、(x+2) 2=310. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )
A、25π+24 B、5π+24 C、25π D、5π9. 用配方法解方程x2+4x+1=0时,配方结果正确的是( )A、(x﹣2)2=5 B、(x﹣2) 2=3 C、(x+2) 2=5 D、(x+2) 2=310. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )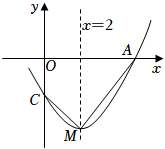 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、解答题(共8题,共72分)
-
11.(1)、解不等式组 , 并写出该不等式组的最小整数解.(2)、先化简,再求值:(+1)÷ , 其中a=4sin30°﹣(π﹣3)0 .12. 神舟十四号载人飞船的成功发射,再次引发校园科技热.光明中学准备举办“我的航天梦”科技活动周,在全校范围内邀请有兴趣的学生参加以下四项活动,A:航模制作;B:航天资料收集;C:航天知识竞赛;D:参观科学馆.为了了解学生对这四项活动的参与意愿,学校随机调查了该校有兴趣的m名学生(每名学生必选一项且只能选择一项),并将调查的结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
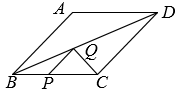
(1)、 ▲ , ▲ ;并补全条形统计图:(2)、根据抽样调查的结果,请估算全校1800名学生中,大约有多少人选择参观科学馆;(3)、在选择A项活动的10人中,有甲、乙、丙、丁四名女生,现计划把这10名学生平均分成两组进行培训,每组各有两名女生,则甲、乙被分在同一组的概率是多少?13. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证: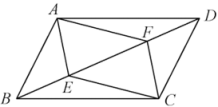 (1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.14. 如图,在平面直角坐标系中,菱形的顶点在轴上, , 两点的坐标分别为 , , 直线:与反比例函数的图象交于 , 两点.
(1)、△ABE≌△CDF;(2)、四边形AECF是平行四边形.14. 如图,在平面直角坐标系中,菱形的顶点在轴上, , 两点的坐标分别为 , , 直线:与反比例函数的图象交于 , 两点.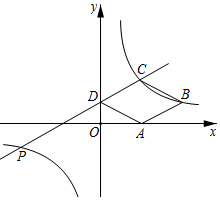 (1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.15. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.
(1)、求该反比例函数的解析式及的值;(2)、判断点是否在该反比例函数的图象上,并说明理由.15. 2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,是垂直于工作台的移动基座,、为机械臂,m,m,m, . 机械臂端点到工作台的距离m.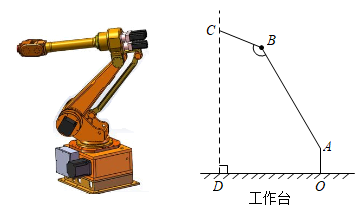 (1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )16. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.
(1)、求、两点之间的距离;(2)、求长.(结果精确到0.1m,参考数据: , , , )16. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.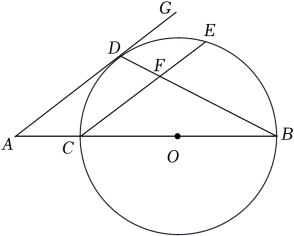 (1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.17. 在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点P的“倾斜系数”k.
(1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.17. 在平面直角坐标系中, 是第一象限内一点,给出如下定义: 和 两个值中的最大值叫做点P的“倾斜系数”k.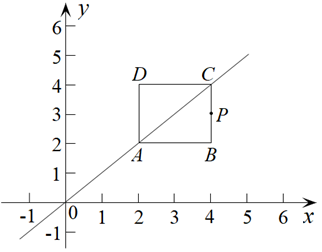 (1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;
(1)、求点 的“倾斜系数”k的值;(2)、①若点 的“倾斜系数” ,请写出a和b的数量关系,并说明理由;②若点 的“倾斜系数” ,且 ,求OP的长;
(3)、如图,边长为2的正方形ABCD沿直线AC: 运动, 是正方形ABCD上任意一点,且点P的“倾斜系数” ,请直接写出a的取值范围.18. 在平面直角坐标系中,直线y=mx-2m与x轴,y轴分别交于A,B两点,顶点为D的抛物线y=-x2+2mx-m2+2与y轴交于点C.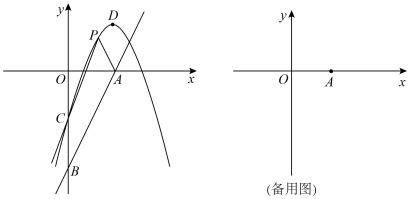 (1)、如图,当m=2时,点P是抛物线CD段上的一个动点.
(1)、如图,当m=2时,点P是抛物线CD段上的一个动点.①求A,B,C,D四点的坐标;
②当△PAB面积最大时,求点P的坐标;
(2)、在y轴上有一点M(0,m),当点C在线段MB上时,①求m的取值范围;
②求线段BC长度的最大值.
三、填空题(每空3分,共18分)
-
19. 已知x,y是实数,且满足y=++ , 则的值是 .20. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 .
 21. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
21. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.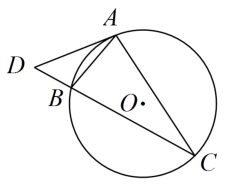 22. 喜迎党的二十大召开,学校推荐了四部影片:、香山叶正红、建党伟业、建军大业 . 甲、乙同学用抽卡片的方式决定本班观看哪部,四张卡片正面分别是上述影片剧照,除此之外完全相同.将这四张卡片背面朝上,甲随机抽出一张并放回,洗匀后,乙再随机抽出一张,则两人恰好抽到同一部的概率是 .
22. 喜迎党的二十大召开,学校推荐了四部影片:、香山叶正红、建党伟业、建军大业 . 甲、乙同学用抽卡片的方式决定本班观看哪部,四张卡片正面分别是上述影片剧照,除此之外完全相同.将这四张卡片背面朝上,甲随机抽出一张并放回,洗匀后,乙再随机抽出一张,则两人恰好抽到同一部的概率是 .