浙江省舟山市金衢山五校联考2022-2023学年九年级下学期第一次学业水平数学质量监测卷

试卷更新日期：2023-03-24 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. $- \frac{1}{2023}$ 的相反数是（）

A、-2023 B、 $\frac{1}{2023}$ C、 $- \frac{1}{2023}$ D、2023

查看试题解析
2. 在六张卡片上分别写有5， $- \frac{22}{7}$ ， 3.1415， $π$ ， 0， $\sqrt{2}$ 六个数，从中随机抽取一张，卡片上的数为无理数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
3. 下列图标中，不属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列命题中：①若 $a > b$ ，则 $a^{2} > b^{2}$ ；②若 $| a | = b$ ，则 $a = b$ ；③对顶角相等；④两边一角对应相等的两个三角形全等．是真命题的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图是一个由5个相同的正方体组成的立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 如图，正方形 $A B C D$ 的边长为8，在各边上顺次截取 $A E = B F = C G = D H = 6$ ，则四边形 $E F G H$ 的面积是（）

A、34 B、36 C、40 D、100

查看试题解析
7. 如图，矩形 $A B C D$ 中， $A B = 4 ， B C = 3$ ， F是 $A B$ 中点，以点A为圆心， $A D$ 为半径作弧交 $A B$ 于点E，以点B为圆心， $B F$ 为半径作弧交 $B C$ 于点G，则图中阴影部分面积的差 $S_{1} - S_{2}$ 为（）

A、 $12 - \frac{13 π}{4}$ B、 $12 - \frac{9 π}{4}$ C、 $6 + \frac{13 π}{4}$ D、6

查看试题解析
8. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{matrix} x + 2 y = a - 3 \\ 3 x - y = 2 a \end{matrix}$ ，有下列说法：①当 $a = 2$ 时，方程的两根互为相反数；②不存在自然数 $a$ ，使得 $x$ ， $y$ 均为正整数；③ $x$ ， $y$ 满足关系式 $x - 5 y = 6$ ；④当且仅当 $a = - 5$ 时，解得 $x$ 为 $y$ 的2倍．其中正确的是（）

A、①②③④ B、①③④ C、②③ D、①②④

查看试题解析
9. 如果 $(x + m) (x - 5) = x^{2} - 3 x + k$ ，那么 $k$ 、 $m$ 的值分别是（）．

A、 $k = 10$ ， $m = 2$ B、 $k = 10$ ， $m = - 2$ C、 $k = - 10$ ， $m = 2$ D、 $k = - 10$ ， $m = - 2$

查看试题解析
10. 二次函数 $y = a x^{2} + 4 x + 1$ （ $a$ 为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq m$ 的任意一个 $x$ 的值，都有 $- 2 ≤ y ≤ 2$ ，则 $m$ 的最大值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、2 D、 $\frac{3}{2}$

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

11. 已知 $a b = 3$ ， $a + b = 4$ ，则代数式 $a^{3} b + a b^{3}$ 的值为．

查看试题解析
12. 一个n边形的内角和是540°，那么n= ．

查看试题解析
13. 若最简根式 $\sqrt{- 2 m + 9}$ 与 $\sqrt{5 m - 5}$ 是同类二次根式，则m= ．

查看试题解析
14. 如图，在 $△ A B C$ 中， $∠ A B C = 30 °$ ， $A B = A C = 2 \sqrt{3}$ ，点D是边 $B C$ 上的点，将 $△ A C D$ 沿 $A D$ 折叠得到 $△ A E D$ ，线段 $A E$ 与边 $B C$ 交于点F．若 $∠ C D E$ 为直角，则 $C D$ 的长是．

查看试题解析
15. 如图，在平面直角坐标系中，点A，B在反比例函数 $y = \frac{k}{x}$ 图像上， $B C ⊥ x$ 轴于点C， $A D ⊥ y$ 轴于点D，连结 $A O ， A B$ ，若 $O D = 3 B C = 3 ， A O = A B$ ，则k的值为．

查看试题解析
16. 如图，点 $P$ 是反比例函数 $y_{1} = \frac{3 \sqrt{2}}{x} (x > 0)$ 上一点，过点 $P$ 作 $x$ 轴、 $y$ 轴的垂线，分别交反比例函数 $y_{2} = \frac{k}{x} (k > 0)$ 的图象于点 $A$ 、 $B$ ，若 $O P = 2 A B$ ， $∠ O B A = 90 °$ ，则点 $P$ 的坐标为．

查看试题解析

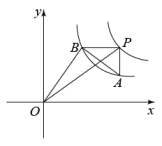
三、解答题（第17～18题每小题6分，第19题8分，第20题6分，第21题8分，第22，23题每小题10分，第24题12分，共66分）

17.

(1)、计算 $： {(\sqrt{2} - 1)}^{0} + {(- 1)}^{2023} + {(\frac{1}{3})}^{- 1} - 2 sin 30 °$ ．

(2)、先化简，再求值： $3 (2 a^{2} - 2 b) - (a^{2} - 6 b + 1)$ ﹐其中 $a = 1$ ， $b = 2023$ ．

查看试题解析
18. 以下是欣欣解方程： $\frac{x + 2}{3} - \frac{2 x - 1}{2} = 1$ 的解答过程：
解：去分母，得 $2 (x + 2) - 3 (2 x - 1) = 1$ ；……………………①

去括号： $2 x + 2 - 6 x + 3 = 1$ ；………………………………… ②

移项，合并同类项得： $- 4 x = - 4$ ；………………………………③

解得： $x = 1$ ． …………………………………………………………④

(1)、欣欣的解答过程在第几步开始出错?（请写序号即可）

(2)、请你完成正确的解答过程．

查看试题解析
19. 为深入学习贯彻党的二十大大精神，引领广大职工准确把握党的二十大报告的丰富内涵、精神实质、实践要求，我区教育工会开展了学习二十大知识竞赛活动，根据竞赛活动的成绩划分了四个等级：A．合格，B．良好，C．优秀，D．非常优秀．现随机抽查部分竞赛成绩的数据进行了整理、绘制成部分统计图：

请根据图中信息，解答下列问题：

(1)、填空： $a =$ %，“优秀”对应扇形的圆心角度数为；

(2)、请你补全条形统计图；

(3)、若我区有8000名教职工，请你估计其中“优秀”和“非常优秀”的教职工共有多少人？

查看试题解析
20. 如图，在矩形 $A B C D$ 中，点E为边 $A B$ 上的一动点（点E不与点A，B重合），连接 $D E$ ，过点C作 $C F ⊥ D E$ ，垂足为F．

(1)、求证： $△ A D E$ ∽ $△ F C D$ ；

(2)、若 $A D = 6$ ， $t a n ∠ D C F = \frac{1}{3}$ ，求 $A E$ 的长．

查看试题解析
21. 如图1是一个简易手机支架，由水平底板 $D E$ 、侧支撑杆 $B D$ 和手机托盘长 $A C$ 组成，侧面示意图如图2所示.已知手机托盘长 $A C = 10 c m$ ，侧支撑杆 $B D = 10 c m$ ， $∠ C B D = 75 °$ ， $∠ B D E = 60 °$ ，其中点A为手机托盘最高点，支撑点B是 $A C$ 的中点，手机托盘 $A C$ 可绕点B转动，侧支撑杆 $B D$ 可绕点D转动.

(1)、如图2，求手机托盘最高点A离水平底板 $D E$ 的高度h（精确到 $0.1 c m$ ）.

(2)、如图3，当手机托盘 $A C$ 绕点B逆时针旋转 $15 °$ 后，再将 $B D$ 绕点D顺时针旋转 $α$ ，使点C落在水平底板 $D E$ 上，求 $α$ （精确到0.1 $°$ ）.（参考数据： $t a n 26.6 ° \approx 0.5$ ， $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
22. 某商场第1次用39万元购进 $A$ ， $B$ 两种商品，销售完后获得利润6万元，它们的进价和售价如表（总利润=单价利润×销售量）：

价格商品

进价（元/件）

售价（元/件）

$A$

1200

1350

$B$

1000

1200

(1)、该商场第1次购进 $A$ ， $B$ 两种商品各多少件？

(2)、商场第2次以原进价购进 $A$ ， $B$ 两种商品，购进 $A$ 商品的件数不变，而购进 $B$ 商品的件数是第1次的2倍， $A$ 商品按原售价销售，而 $B$ 商品打折销售，若两种商品销售完毕，要使得第2次经营活动获得利润等于5.4万元，则 $B$ 种商品是按几折销售的？

查看试题解析
23. 如图1，已知 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 10$ ， $B C = m$ ，点 $D$ 在 $A C$ 上，连结 $B D$ ，作 $C E ⊥ A B$ ，交 $△ B D C$ 的外接圆 $⊙ O$ 于点 $E$ ，连结 $D E$ 和 $B E$ ．

(1)、求证： $∠ B D E = ∠ A$ ．在思考的过程中，小浔同学得到了如下思维分析图：

请根据上述思维分析图，写出完整证明过程．

(2)、如图2，若点 $D$ 是 $A C$ 中点．
①当 $m = 6$ 时，求 $B E$ 的长；

②是否存在 $m$ 的值，使得 $C E$ 恰好是 $⊙ O$ 的直径，若存在，请求出 $m$ 的值，若不存在，请说明理由．

查看试题解析
24. 如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $P$ 是 $B C$ 上一点（不与点 $B$ ， $C$ 重合），过点 $P$ 作 $P D ⊥ A B$ 于点 $D$ ，连接 $C D$ 并延长交 $△ A B C$ 的外接圆于点 $E$ ，连接 $E A$ ， $E B$ ， $A P$ .

(1)、求证： $∠ D P B = ∠ C E B$ .

(2)、若 $C D^{2} = C P \cdot C B$ ，求证： $B D = B E$ .

(3)、如图2， $A C = 2$ ， $B C = 4$ .
①若 $t a n ∠ E C B = \frac{1}{3}$ ，求 $A P$ 的长.
②求 $A P \cdot D E$ 的最大值.

查看试题解析

价格商品	进价（元/件）	售价（元/件）
$A$	1200	1350
$B$	1000	1200