浙江省舟山市定海二中2022-2023学年九年级下学期3月份素养监测数学试题
试卷更新日期:2023-03-24 类型:月考试卷
一、选择题(每小题3分,每小题仅有一个正确选项,共30分.)
-
1. 2023的绝对值为( )A、 2023 B、-2023 C、2023 D、-20232. 一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的众数是( )A、6 B、7 C、8 D、93. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、  D、
D、 4. “多少事,从来急;天地转,光阴迫.一万年太久,只争朝夕.”伟人毛泽东通过这首《满江红·和郭沫若同志》告诉我们青年学生:要珍惜每分每秒;努力工作,努力学习.一天时间为86400秒,用科学记数法表示这一数字是A、864×102 B、86.4×103 C、8.64×104 D、0.0.864×1055. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2, DE=8,则AB的长为( )
4. “多少事,从来急;天地转,光阴迫.一万年太久,只争朝夕.”伟人毛泽东通过这首《满江红·和郭沫若同志》告诉我们青年学生:要珍惜每分每秒;努力工作,努力学习.一天时间为86400秒,用科学记数法表示这一数字是A、864×102 B、86.4×103 C、8.64×104 D、0.0.864×1055. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2, DE=8,则AB的长为( ) A、4 B、6 C、7 D、86. 下列运算正确的是( )A、 B、 C、 D、7. 如图,将ΔABC沿BC方向平移3cm得到ΔDEF,若ΔABC的周长为16cm,则四边形ABFD的周长为( )
A、4 B、6 C、7 D、86. 下列运算正确的是( )A、 B、 C、 D、7. 如图,将ΔABC沿BC方向平移3cm得到ΔDEF,若ΔABC的周长为16cm,则四边形ABFD的周长为( )
 A、18cm B、20cm C、22cm D、24cm8. 一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )A、3 B、3.5 C、4 D、4.59. 如图,在一张矩形纸片ABCCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
A、18cm B、20cm C、22cm D、24cm8. 一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )A、3 B、3.5 C、4 D、4.59. 如图,在一张矩形纸片ABCCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )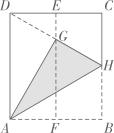 A、 B、 C、 D、10. 当时,二次函数有最大值4,则实数m的值为( )A、 B、 C、 D、
A、 B、 C、 D、10. 当时,二次函数有最大值4,则实数m的值为( )A、 B、 C、 D、二、填空题(每小题4分,共24分)
-
11. 分解因式: = .
12. 一个正多边形的每个内角都为135°,那么该正多边形的边数为 .13. 在+()=0的括号中添加一个实数,使方程有两个相等的实数根。14. 如图,在ΔABC中,AB=2 AC=4,将ΔABC绕点C按逆时针方向旋转得到ΔA'B'C使CB'//AB,分别延长AB,CA'相交于点D,则线段BD的长为。 15. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ((0°<θ<90°))得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°点M的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为。
15. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ((0°<θ<90°))得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°点M的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为。 16. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则下列结论:①CE=CF;②线段EF的最小值为;③若点F恰好落在弧BC上,则AD=④当AD=2时,与半圆相切;⑤当点D从点A运动到点B时,线段 EF扫过的面积是。其中正确结论的序号是。
16. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则下列结论:①CE=CF;②线段EF的最小值为;③若点F恰好落在弧BC上,则AD=④当AD=2时,与半圆相切;⑤当点D从点A运动到点B时,线段 EF扫过的面积是。其中正确结论的序号是。
三、解答题(第17~18题每小题6分,第19题8分,第20题6分,第21题8分,第22,23题每小题10分,第24题12分,共66分)
-
17. 计算(1)、(2)、化简:18. 老师设计了接力游戏,用合作的方式完成分式化简,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简. 过程如图所示:
 (1)、接力中,自己负责的一步出现错误的同学是;(2)、请你书写正确的化简过程,并在“-1,0,1”中选择一个合适的数代入求值.19. 央视“经典咏流传”开播以来受到社会广泛关注。我校就“中华文化我传承-地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图。请你根据统计图所提供的信息解答下列问题:
(1)、接力中,自己负责的一步出现错误的同学是;(2)、请你书写正确的化简过程,并在“-1,0,1”中选择一个合适的数代入求值.19. 央视“经典咏流传”开播以来受到社会广泛关注。我校就“中华文化我传承-地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图。请你根据统计图所提供的信息解答下列问题:图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”。
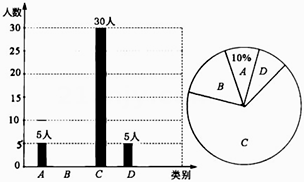 (1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若我校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率。20. 已知:如图,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)、被调查的总人数是人,扇形统计图中C部分所对应的扇形圆心角的度数为.(2)、补全条形统计图;(3)、若我校共有学生1800人,请根据上述调查结果,估计该校学生中A类有人;(4)、在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率。20. 已知:如图,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF. (1)、求证:ΔDOE≌ΔBOF.(2)、当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.21. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度,某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:sin 70°≈0.94 cos 70°≈0.34 tan 70°≈2.75, ≈1.73)
(1)、求证:ΔDOE≌ΔBOF.(2)、当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.21. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度,某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1m.参考数据:sin 70°≈0.94 cos 70°≈0.34 tan 70°≈2.75, ≈1.73)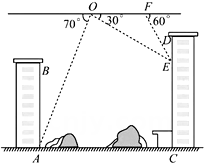
 22. 某文具店最近有A,B两款纪念册比较畅销.该店购进A款纪念册5本和B款纪念册4本共需156元,购进A款纪念册3本和B款纪念册5本共需130元.在销售中发现:A款纪念册售价为32元/本时,每天的销售量为40本,每降低1元可多售出2本;B款纪念册售价为22元/本时,每天的销售量为80本,B款纪念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示:
22. 某文具店最近有A,B两款纪念册比较畅销.该店购进A款纪念册5本和B款纪念册4本共需156元,购进A款纪念册3本和B款纪念册5本共需130元.在销售中发现:A款纪念册售价为32元/本时,每天的销售量为40本,每降低1元可多售出2本;B款纪念册售价为22元/本时,每天的销售量为80本,B款纪念册每天的销售量与售价之间满足一次函数关系,其部分对应数据如下表所示:售价(元/本)
……
22
23
24
25
……
每天销售量(本)
……
80
78
76
74
……
(1)、求A,B两款纪念册每本的进价分别为多少元?(2)、该店准备降低每本A款纪念册的利润,同时提高每本B款纪念册的利润,且这两款纪念册每天销售总数不变,设A款纪念册每本降价m元;①直接写出B款纪念册每天的销售量(用含m的代数式表示);
②当A款纪念册售价为多少元时,该店每天所获利润最大,最大利润是多少?
23. 已知抛物线.(1)、若 , , 求该抛物线与轴公共点的坐标;(2)、若 , 且当时,抛物线与x轴有且只有一个公共点,求的取值范围;(3)、若 , 且时,对应的;时,对应的 , 试判断当时,抛物线与轴是否有公共点?若有,请证明你的结论;若没有,请说明理由.24. 如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E. (1)、求证:∠BPD=∠BAC.(2)、连接EB,ED,当 tan∠MAN=2 AB=时,在点P的整个运动过程中.
(1)、求证:∠BPD=∠BAC.(2)、连接EB,ED,当 tan∠MAN=2 AB=时,在点P的整个运动过程中.①若∠BDE=45°,求PD的长.
②若ΔBED为等腰三角形,求直接写出所有满足条件的BD的长.
(3)、连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记ΔOFPP的面积为S1 , ΔCFE 的面积为S2 , 请求出的值.