浙江省义乌2022-2023学年七年级下学期第一次独立作业数学试卷

试卷更新日期：2023-03-24 类型：月考试卷

进入出卷网下载

一、选择题（共10小题，每小题3分，满分30分）

1. 如图，直线a，b被c所截，则∠1与∠2是（）

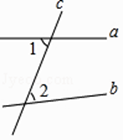A、同位角 B、内错角 C、同旁内角 D、邻补角

查看试题解析
2. 已知方程mx＋2y＝－2，当x＝3时y＝5，那么m为（）

A、 $\frac{8}{3}$ B、 $- \frac{8}{3}$ C、－4 D、 $\frac{8}{5}$

查看试题解析
3. 已知二元一次方程5x＋（k－1）y－7＝0的一个解是 ${\begin{array}{l} x = 1 \\ y = - 3 \end{array}$ ，求k的值（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{5}{3}$ D、 $- \frac{5}{3}$

查看试题解析
4. 下列方程：①x＋y＝1；② $2 x - \frac{y}{2} = 1$ ；③x²＋y²＝1；④5（x＋y）＝7（x－y）；⑤x²＝1；⑥ $x + \frac{1}{2} = 4$ ，其中是二元一次方程的是（）

A、① B、①②④ C、①③ D、①②④⑥

查看试题解析
5. 如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（　　）

A、15° B、25° C、35° D、65°

查看试题解析
6. 若方程组 ${\begin{array}{l} 3 x + y = 1 + 3 a \\ x + 3 y = 1 - a \end{array}$ 的解满足x＋y＝0，则a的值为（）

A、－1 B、1 C、0 D、无法确定

查看试题解析
7. 一副三角板按如图所示的位置摆放，若BC∥DE，则∠1的度数是（）

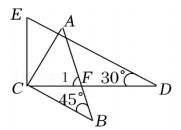A、65° B、70° C、75° D、80°

查看试题解析
8. 如图，有下列判定，其中正确的有（）

①若∠1＝∠3，则AD∥BC；②若AD∥BC，则∠1＝∠2＝∠3；③若∠1＝∠3，AD∥BC，则∠1＝∠2；④若∠C+∠3＋∠4＝180°，则AD∥BC．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ ，下列结论中正确的有几个（）
①当这个方程组的解x，y的值互为相反数时，a＝－2；②当a＝1时，方程组的解也是方程x＋y＝4＋2a的解；③无论a取什么实数，x＋2y的值始终不变；④若用x表示y，则 $y = - \frac{x}{2} + \frac{3}{2}$ ；

A、1 B、2 C、3 D、4

查看试题解析
10. 如图， $D C ∥ A B$ ， AE⊥EF，E在BC上，过E作EC⊥DC，EG平分∠FEC，ED平分∠AEC．若∠EAD＋∠BAD＝180°，∠EDA＝3∠CEG，则下列结论：①∠EAB＝2∠FEG；②∠AED＝45°＋∠GEF；③∠EAD＝135°－4∠GEC；④∠EAB＝15°，其中正确的是（）

A、①②③④ B、①③④ C、①②④ D、①②③

查看试题解析

二、填空题（每小题3分，共18分）

11. 把方程7x－y＝15改写成用含x的式子表示y的形式为y＝．

查看试题解析
12. 已知－2xⁿ^－^3my³与3x⁷y^m^＋ⁿ是同类项，则mⁿ的值是．

查看试题解析
13. 如图，将一张长方形纸片按如图所示折叠，如果∠1＝55°，那么∠2＝°.

查看试题解析
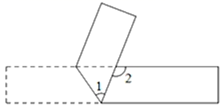14. 如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置，AB＝9，DO＝4，平移距离为6，则阴影部分面积为．

查看试题解析
15. 已知关于x，y的二元一次方程3x－4y＋mx＋2m＋8＝0，若无论m取任何实数，该二元一次方程都有一个固定的解，则这个固定的解为．

查看试题解析
16. 如图消防云梯，其示意图如图1所示，其由救援台AB，延展臂BC（B在C的左侧）、伸展主臂CD，支撑臂EF构成，在作业过程中，救援台AB、车身GH及地面MN三者始终保持水平平行．为了参与一项高空救援工作，需要进行作业调整，如图2，使得延展臂BC与支摚臂EF所在直线互相垂直，且∠EFH＝69°，则这时展角∠ABC＝．

查看试题解析

三、解答题（第17，18，19，20，21，22每题6分，23题8分，第24题8分）

17. 解方程组：

(1)、 ${\begin{array}{l} y = 3 x - 5 \\ - x + 2 y = 15 \end{array}$

(2)、 ${\begin{array}{l} x - 2 y = - 4 ， \\ 3 x + 4 y = 18 ． \end{array}$

查看试题解析
18. 已知：如图，∠B＋∠3＝90°，∠B＋∠E＝90°，∠1＝∠E，求证：AD平分∠BAC，
请完善证明过程，并在括号内填上相应依据：

证明：∵∠B＋∠3＝90°，∠B＋∠E＝90°，（        ）

∴▲ ＝▲ ，（        ）

∴ $A D ∥ E G$ ，（         ）

∴∠2＝∠1，（         ）

∵∠E＝∠1（已知），

∴▲ ＝▲ ，（         ）

∴AD平分∠BAC．（        ）

查看试题解析
19. 如图，在每个小正方形边长为1的网格中，平移三角形ABC，并将三角形ABC的一个顶点A平移到D处.

(1)、请你作出平移后的三角形DEF.

(2)、请求出三角形DEF的面积.

查看试题解析
20. 如图，已知CF $∥$ AG，E是直线AB上的一点，CE平分∠ACD，射线CF⊥CE，∠2＝58°.

(1)、求∠ACE的度数；

(2)、若∠1＝32°，说明：AB $∥$ CD.

查看试题解析
21. 在解方程组 ${\begin{array}{l} a x - b y = 13 \\ c x - y = 4 \end{array}$ 时，甲同学因看错了b的符号，从而求得解为 ${\begin{matrix} x = 3 \\ y = 2 \end{matrix}$ ，乙同学因看漏了c，从而求得解为 ${\begin{matrix} x = 5 \\ y = 1 \end{matrix}$ ，试求(b＋c)^a的值．

查看试题解析
22. 已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨，某物流公司现有26吨货物，计划A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：

(1)、1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？

(2)、请你帮该物流公司设计租车方案：

(3)、若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱车方案，并求出最少租车费．

查看试题解析
23. 【方法体验】已知方程组 ${\begin{matrix} 2018 x - 2017 y = 20 ， ① \\ 2019 x + 2018 y = 500. ② \end{matrix}$ 求4037x＋y的值．小明同学发现解此方程组代入求值很麻烦!后来他将两个方程直接相加便迅速解决了问题．请你体验一下这种快捷思路，写出具体解题过程：
【方法迁移】根据上面的体验，填空：

已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 则3x＋y－z＝．

【探究升级】已知方程组 ${\begin{array}{l} x + 2 y + 3 z = 10 \\ 4 x + 3 y + 2 z = 15 \end{array}$ 求－2x＋y＋4z的值．小明凑出

“－2x＋y＋4z＝2•（x＋2y＋3z）＋（－1）•（4x＋3y＋2z）＝20－15＝5”，虽然问题获得解决，但他觉得凑数字很辛苦!他问数学老师丁老师有没有不用凑数字的方法，丁老师提示道：假设－2x＋y＋4z＝m•（x＋2y＋3z）＋n•（4x＋3y＋2z），对照方程两边各项的系数可列出方程组 ${\begin{matrix} m + 4 n = - 2 \\ 2 m + 3 n = 1 \\ 3 m + 2 n = 4 \end{matrix}$ ，它的解就是你凑的数!

根据丁老师的提示，填空：

2x＋5y＋8z＝（x＋2y＋3z）＋（4x＋3y＋2z）

【巩固运用】已知2a－b＋kc＝4，且a＋3b＋2c＝－2，当k为时，8a＋3b－2c为定值，此定值是．（直接写出结果）

查看试题解析
24. 如图1， $A B ∥ C D$ ，点E，F分别在直线CD，AB上，∠BEC＝2∠BEF，过点A作AG⊥BE的延长线交于点G，交CD于点N，AK平分∠BAG，交EF于点H，交BE于点M．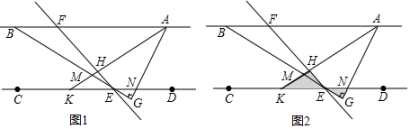

(1)、直接写出∠AHE，∠FAH，∠KEH之间的关系：．

(2)、若 $∠ B E F = \frac{1}{2} ∠ B A K$ ，求∠AHE．

(3)、如图2，在（2）的条件下，将△KHE绕着点E以每秒5°的速度逆时针旋转，旋转时间为t，当KE边与射线ED重合时停止，则在旋转过程中，当△KHE的其中一边与△ENG的某一边平行时，直接写出此时t的值.

查看试题解析