四川省达州市宣汉县2022-2023学年七年级下学期第一次月考数学试题
试卷更新日期:2023-03-24 类型:月考试卷
一、选择题(每小题3分,共30分)
-
1. 若 ,那么 的值是 ( )A、10 B、52 C、20 D、322. 同一平面内的三条直线满足a⊥b,b⊥c,则下列式子成立的是( )A、a∥c B、a∥b C、b∥c D、a⊥c3. 在下列的计算中正确的是( )A、2x+3y=5xy B、(a+2)(a-2)=a2+4 C、a2•ab=a3b D、(x-3)2=x2+6x+94. 下列说法正确的是( )A、两点之间的距离是两点间的线段 B、同一平面内,过一点有且只有一条直线与已知直线平行 C、与同一条直线垂直的两条直线也垂直 D、同一平面内,过一点有且只有一条直线与已知直线垂直5.
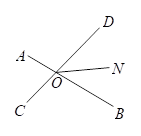
将一副直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为( )
 A、140° B、160° C、170° D、150°6. 长方形一边长为另一边比它小则长方形面积为 ( )A、 B、 C、 D、7.
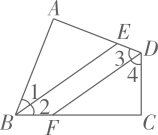
A、140° B、160° C、170° D、150°6. 长方形一边长为另一边比它小则长方形面积为 ( )A、 B、 C、 D、7.如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
 A、①②③④ B、①②④ C、①③④ D、①②③8. 下列多项式乘法,能用平方差公式计算的是 ( )A、 B、 C、 D、9. 如下图(1),边长为a的大正方形中一个边长为b的小正方形,小明将图(1)的阴影部分拼成了一个矩形,如图(2).这一过程可以验证( )
A、①②③④ B、①②④ C、①③④ D、①②③8. 下列多项式乘法,能用平方差公式计算的是 ( )A、 B、 C、 D、9. 如下图(1),边长为a的大正方形中一个边长为b的小正方形,小明将图(1)的阴影部分拼成了一个矩形,如图(2).这一过程可以验证( ) A、a2+b2-2ab=(a-b)2 B、a2+b2+2ab=(a+b)2 C、2a2-3ab+b2=(2a-b)(a-b) D、a2-b2=(a+b) (a-b)10. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An=( )
A、a2+b2-2ab=(a-b)2 B、a2+b2+2ab=(a+b)2 C、2a2-3ab+b2=(2a-b)(a-b) D、a2-b2=(a+b) (a-b)10. 如图,已知A1B∥AnC,则∠A1+∠A2+…+∠An=( ) A、180°n B、(n+1)180° C、(n-1)180° D、(n-2)180°
A、180°n B、(n+1)180° C、(n-1)180° D、(n-2)180°二、填空题
-
11.(1)、计算: .(2)、计算: .12. 如图,已知直线与交于点 , 平分 , 若 , 则 的度数为 .
 13. 已知:则x+y=.14. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西.
13. 已知:则x+y=.14. 如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西. 15. 已知a是-2的相反数,且|b+1|=0,则[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)的值为 .16. 如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为 .
15. 已知a是-2的相反数,且|b+1|=0,则[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)的值为 .16. 如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为 .
三、解答题
-
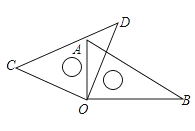
17. 计算:(1)、(a3)3·(a4)3;(2)、(-a2)3·(b3)2·(ab)4.(3)、(3x-1)(2x-1);(4)、5x(x+1)2-(2x+3)(2x-3).18. 先化简,再求值:(1)、[(x+2y2)2-(x+y2)(x-y2)-5y4]÷2y,其中x=-2,y=;(2)、(2a+b)(2a-b)-(a-2b)2+(6a4-4a3)÷(-2a2),其中a= , b=1.19. 如图,AO⊥CO,BO⊥DO,∠BOC=43°,求∠AOD和∠AOB的度数.
 20. 已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。求证:AD∥BE。
20. 已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。求证:AD∥BE。
证明:∵AB∥CD(已知)
∴∠4=∠ ▲ ( )
∵∠3=∠4(已知)
∴∠3=∠ ▲ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF( )
即∠ ▲ =∠ ▲
∴∠3=∠ ▲ ( )
∴AD∥BE( )
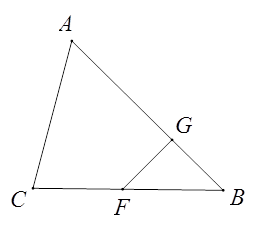
21. 若 , , 求下列各式的值:(1)、 ;(2)、22. 如图,已知 , , 试说明: . (写出推理过程,不写理由) 23. 如图,在四边形中, , , 平分 , 平分 , 则与有何位置关系?试说明理由.
23. 如图,在四边形中, , , 平分 , 平分 , 则与有何位置关系?试说明理由.