浙江省杭州市临平区2022-2023学年九年级下学期3月月考数学试卷

试卷更新日期：2023-03-24 类型：月考试卷

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．

1. 下列等式正确的是（）

A、( $\sqrt{3}$ )²＝3 B、 $\sqrt{(- 3)^{2}}$ ＝－3 C、 $\sqrt{3^{3}}$ ＝3 D、( $- \sqrt{3}$ )²＝－3

查看试题解析
2. 如图，AB∥CD，AD，BC相交于点O．若AB＝1，CD＝2，BO∶CO＝（）

A、1∶2 B、1∶4 C、2∶1 D、4∶1

查看试题解析
3. 两枚同样的硬币同时抛出，落地后一个正面朝上、一个反面朝上的概率是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
4. 如图，边长相等的正五边形和正六边形如图拼接在一起，则∠ABC的度数为（）

A、22 B、23 C、24 D、25

查看试题解析
5. 在Rt△ABC中，∠C＝90°，∠B＝35°，AB＝7，则BC的长为（）

A、7sin 35° B、7cos 35° C、7tan 35° D、 $\frac{7}{\cos 35 °}$

查看试题解析
6. 如图，在⊙O中，AB是直径，CD是弦．若∠BCD＝44°，则∠ABD＝（）

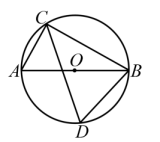A、40° B、44° C、45° D、46°

查看试题解析
7. 如图，已知△ABC，点D是BC边中点，且∠ADC＝∠BAC．若BC＝6，则AC＝（）

A、3 B、4 C、4 $\sqrt{2}$ D、3 $\sqrt{2}$

查看试题解析

8. 已知二次函数y＝ax²＋bx＋c，y与x的部分对应值为：

x	…	－2	－1	0	1	2	…
y	…	－1	2	3	2	？	…

关于此函数的图象和性质，下列说法正确的是（）

A、当x＞0时，函数图象从左到右上升 B、抛物线开口向上 C、方程ax²＋bx＋c＝0的一个根在－2与－1之间 D、当x=2时，y=1

查看试题解析

9. 如图，⊙O经过△ABC的顶点C，与边CB，CA分别交于点M，N，与AB边相切．若∠BCA＝60°，∠A＝45°，AC＝4，则线段MN长度的最小值是（）

A、3 B、2 $\sqrt{3}$ C、2 $\sqrt{2}$ D、 $\sqrt{6}$

查看试题解析
10. 如图，在△ABC中，∠BAC＝90°，AB＝AC＝12，点P在边AB上，D，E分别为BC， PC的中点，连接DE．过点E作BC的垂线，与BC，AC分别交于F，G两点．连接DG，交PC于点H．有以下判断：①∠EDC＝45°；② DG⊥PE，且DG＝PE； ③当AP＝6时，△APG的面积为9；④ $\frac{C H}{C E}$ 的最大值为 $\frac{\sqrt{2} + 1}{2}$ ．其中正确的是（）

A、①③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题：本题有6个小题，每小题4分，共24分．

11. 某平台进行“天宫课堂”中国空间站全程直播．某一时刻观看人数达到3790000人．用科学记数法表示3790000＝．

查看试题解析
12. 因式分解：a³－4a＝．

查看试题解析
13. 若⊙O中，弦AB的长度是半径的 $\sqrt{2}$ 倍，则弦AB所对圆周角的度数为°．

查看试题解析
14. 已知函数y＝kx，点A(2，4)在函数图象上．当x＝－2时，y＝．

查看试题解析
15. 如图，在△ABC中，AB＝AC＝9，BP＝ $\frac{1}{3}$ BC＝2，D在AC上，且∠APD＝∠B，则CD＝．

查看试题解析
16. 已知二次函数y＝x²＋bx＋c．当－1≤x≤1时，y的取值范围是－1≤y≤1，该二次函数的对称轴为x＝m，则m的值是.

查看试题解析

三、解答题：本题有7小题，共66分．

17. 如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．

(1)、请在图中作出△ABC绕点A逆时针方向旋转90°后得到的图形△A₁B₁C₁ ．

(2)、求点C运动到点C₁所经过的路径的长．

查看试题解析
18. 如图，在△ABC中，AD是角平分线，点E是边AC上一点，且满足∠ADE＝∠B．

(1)、求证：△ADB∽△AED．

(2)、若AE＝3，AD＝5，求AB的长．

查看试题解析
19. 一个不透明的布袋中有完全相同的四个小球，编号为1，2，3，4．甲和乙做游戏：从布袋中随机抽取一个小球，记下标号后，不放回；再从布袋中随机抽取一个小球，记下标号．若两次抽取的小球标号之和为奇数，甲赢；若标号之和为偶数，则乙赢．

(1)、用画树状图或列表的方法，表示出两次取出编号的所有可能；

(2)、判断这个游戏是否公平，并说明理由．

查看试题解析
20. 如图，四边形ABCD内接于⊙O，对角线BD为直径．过点A作AE⊥CD的延长线于点E，且DA平分∠BDE．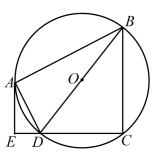

(1)、求证：AE是⊙O的切线；

(2)、若AE＝2 $\sqrt{5}$ ， CD＝8，求⊙O的半径和AD的长．

查看试题解析
21. 如图，在△ABC中，CD是边AB上的中线，∠B是锐角，sinB＝ $\frac{\sqrt{2}}{2}$ ， tanA＝ $\frac{1}{2}$ ， AC＝ $\sqrt{5}$ ．

(1)、求∠B的度数和AB的长．

(2)、求tan∠CDB的值．

查看试题解析
22. 已知二次函数y＝ax²＋bx－4(a，b是常数，且a≠0)的图象过点(3，－1)．

(1)、判断点(2，2－2a)是否也在该函数的图象上，并说明理由．

(2)、若该二次函数的图象与x轴只有一个交点，求该函数的表达式．

(3)、已知点(x₁ ， y₁)和(x₂ ， y₂)在该函数图象上，且当x₁＜x₂≤ $\frac{2}{3}$ 时，始终有y₁＞y₂ ，求a的取值范围．

查看试题解析
23. 如图：

图1 图2

(1)、如图1，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，交AB于点D，DE∥AC，交BC于点E．
①若DE＝1，BD＝ $\frac{3}{2}$ ，求BC的长；

②试探究 $\frac{A B}{A D} - \frac{B E}{D E}$ 是否为定值．如果是，求出这个定值；如果不是，请说明理由．

(2)、如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF＝2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE∥AC，交CB的延长线于点E．记△ACD的面积为S₁ ， △CDE的面积为S₂ ， △BDE的面积为S₃ ．若S₁•S₃＝ $\frac{9}{16}$ S₂² ，求cos∠CBD的值．

查看试题解析